ВСТУП

В математиці можна виділити два могутніх направлення: одне вивчає неперервні об’єкти, друге – дискретні. В реальності є місце і для того і для іншого підходу і часто до вивчення одного і того ж матеріалу можна підходити із різних точок зору. Зрозуміло, що між цими направленнями існує багато зв’язків. Твірні функції одні з них.

Метод твірних функцій – це такий математичний прийом, що дозволяє зводити задачі з теорії чисел, теорії ймовірності та комбінаторики до задач математичного аналізу.

Часто виявляється, що для аналітичного переформулювання задачі, отриманої методом твірних функцій, вдається швидко знайти рішення, в той час, коли інші підходи до вихідної задачі нічого не дають.

Метод характеристичних функцій розробив А.М. Ляпунов для доведення центральної граничної теореми. В подальшому цей метод самостійне значення і виявився ефективним засобом для розв’язування задач з теорії ймовірностей, математичної статистики та в багатьох інших розділах математики.

Метою даної роботи є з’ясування поняття та вивчення видів твірних та характеристичних функцій, а також використання основних понять математичного аналізу при розв’язуванні задач із комбінаторики та математичної статистики.

Об’єктом дослідження є твірні та характеристичні функції.

Метод дослідження полягає у використанні класичних прийомів і теорем з математичного аналізу.

Задачами дослідження є:

1) формулювання означення і формування змісту поняття твірних і характеристичних функцій;

2) ознайомлення з арифметичними операціями над твірними функціями, їх інтегрування і диференціювання, а також властивостями характеристичних функцій;

3) ознайомлення із твірними функціями для відомих послідовностей;

4) доведення теорем про властивості характеристичних функцій, теорему про формулу обертання для характеристичної функції, теорему Леві про критерій слабкої збіжності, теорему про рівномірну збіжність характеристичних функцій та центральну граничну теорему.

Виходячи з вищесказаного, основний матеріал роботи структуровано за трьома розділами, які обрамлені вступом і висновками до роботи, списком використаних літературних джерел з 4 найменувань.

Розділ 1 твірні функції

1.1. Формальні степеневі ряди і твірні функції.

Дії над формальними степеневими рядами. Елементарні твірні функції

1.1.1. Твірні функції і дії над ними

Означення 1.1.1.

Твірною функцією (степеневим рядом) для послідовності будемо називати вираз виду

Або в скороченому вигляді

Якщо всі члени послідовності, починаючи з деякого номеру, дорівнюють нулю, то твірна функція є твірним многочленом.

Твірну функцію, як і звичайну, будемо позначати одною буквою, вказуючи в дужках її аргумент:

Твірна функція представляє послідовність чисел у вигляді ряду по степеням формальної змінної. Тому поряд з терміном «твірна функція» будемо користуватися терміном «формальний степеневий ряд».

Означення 1.1.2. Сумою двох твірних функцій

називається твірна функція

Добутком твірних функцій А і В називається твірна функція

Операція додавання і множення твірних функцій, очевидно, комутативні й асоціативні.

Означення 1.1.3.

Нехай

і

• дві твірні функції, причому

Підстановкою твірної функції В у твірну функцію А називається твірна функція

Якщо, наприклад

Звичайно, якщо обидві функції А і В є многочленами, то означення суми, добутку і підстановки для них співпадає із звичайними означеннями цих операцій для многочленів.

Щоб поближче познайомитись із твірними функціями, потрібно довести важливу теорему.

Теорема 1.1.4 (про обернену функцію)

Нехай функція

така, що , а . Тоді існують такі функції

, ,

і

що

Функції А і С єдині.

Функція А називається лівою оберненою, а функція С- правою оберненою до функції В

Припущення 1.1.5. Нехай

• формальний степеневий ряд, причому .тоді існує єдиний формальний степеневий ряд

……,

такий, що

Доведення. Проведемо доведення по індукції

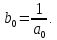
Нехай всі коефіцієнти ряду В а ж до степеня однозначно визначені. Коефіцієнт при визначається з умови

Це лінійне рівняння на коефіцієнт відмінний від нуля. Тому це рівняння має єдиний розв’язок.

1.1.2. Елементарні твірні функції

Кожного разу записувати твірні функції у вигляді ряду незручно. Тому для деяких функцій, які часто зустрічаються, використовується скорочений запис.

Означення 1.1.6.

1. 

1 І довільне комплексне число.

Коефіцієнт при 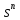в цій твірній функції називається числом комбінацій з елементів по і позначається через

2. 

3. ;

4. ;

5. 

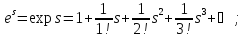
Розклад 1) в означенні 1.1.6 було введено Ньютоном і називається біномом Ньютона. При цілому додатному значенні він співпадає із звичайним означенням степеня бінома. Користуючись цим, ми можемо отримати найпростіші комбінаторні рівності. Підставляючи, наприклад, значення і, отримаємо

, (1.1.3)

(1.1.4)

для будь-якого цілого додатного

Крім того, між введеними елементарними функціями є звичайні співвідношення, які також зв’язані з комбінаторними рівностями. Доведемо, наприклад, що

=1.

Дійсно, вільний член добутку рівний 1, а при коефіцієнт при в добутку рівний

.

Помноживши останній вираз на , отримаємо ліву частину рівності (1.1.4) при , що і доводить наше твердження.