
- •Непрерывность функции. Классификация точек разрыва.
- •Свойства непрерывных функций. Арифметические операции над непрерывными функциями.
- •Точки разрыва и их классификация.
- •Свойства функций, непрерывных в замкнутом промежутке.
- •Равномерная непрерывность функций.
- •Непрерывность и разрывы монотонной функции.
- •Существование и непрерывность обратной функции.
Свойства непрерывных функций. Арифметические операции над непрерывными функциями.
Теорема 1. Пусть функции f(x) и g(x) определены в одном и том же промежутке X и непрерывны в точке х0, то в этой же точке будут непрерывны и функции
f(x)g(x),
f(x)g(x),
![]() (последняя при условии, что g(x0)≠0).
(последняя при условии, что g(x0)≠0).
Доказательство. Вытекает из теорем о пределе алгебраической суммы, произведения и частного двух функций, имеющих пределы.
Докажем, в качестве
примера, непрерывность
![]() .
.
Т.к. функции
f(x)
и g(x)
непрерывны
в точке х0,
то
![]() и
и
![]()
По теореме о пределе частного (т.к. предел знаменателя не нуль), имеем:
![]() ,
а это и означает, что функция
,
а это и означает, что функция
![]() непрерывна в точке х0.ч.т.д.
непрерывна в точке х0.ч.т.д.
Теорема 2. Непрерывность сложной функции.
Пусть даны функции
f
и φ:
![]() .
Если функция φ(х) непрерывна в точке
х0Х,
а функция f(u)
непрерывна в точке u0U,
то функция F=f(φ(x))
будет непрерывна в точке х0.
.
Если функция φ(х) непрерывна в точке
х0Х,
а функция f(u)
непрерывна в точке u0U,
то функция F=f(φ(x))
будет непрерывна в точке х0.
Доказательство 1. Возьмем >0. Т.к. функция f(u) непрерывна в точке u0U, то можно указать такое число σ>0, что для всех uU таких, что |u-u0|<σ выполняется неравенство |f(u)- f(u0)|<.
![]() >0
>0
![]() σ=σ()
σ=σ()
![]() u:
|u-u0|<σ
u:
|u-u0|<σ
![]() |f(σ)-
f(σ0)|<
|f(σ)-
f(σ0)|<
Т.к. φ(х) непрерывна в точке х0Х, то можно указать такое число δ>0, что для всех хХ таких, что |x-x0|<δ выполняется неравенство |φ(х)- φ(x0)|<.
![]() >0
>0
![]() δ=δ()
δ=δ()
![]() x:
|x-x0|<δ
x:
|x-x0|<δ
![]() |φ(х)-
φ(x0)|<.
|φ(х)-
φ(x0)|<.
Из полученных соотношений следует, что если |x-x0|<δ, то функция F=f(φ(x)) определена и выполняется неравенство |f(φ(х))-f(φ(x0))|<. А это и означает непрерывность функции F=f(φ(x)) в точке х0. Ч.т.д.
Доказательство 2. Возьмем произвольную последовательность {xn} такую, что xn→x0, n→. Тогда, в силу непрерывности функции φ(х) в точке х0, будет: φ(хn)→φ(x0), при n→. Т.е. un→u0, n→ (т.к. xnX, то un=φ(хn)U при всех n).
Т.к. un→u0, n→, то в силу непрерывности f(u) в точке u0, имеем:
f(un)→f(u0), n→, т.е. f(φ(xn))→f(φ(x0)), n→, а это и означает непрерывность функции F=f(φ(x)) в точке х0. Ч.т.д.
Из теоремы 2 следует:
![]()
т.е под знаком непрерывной функции можно переходить к пределу.
Пример.
![]()
Примеры непрерывных функций.
1) f(x)С, х(-;+) – непрерывна в любой точке х0(-;+).
Действительно, пусть точка х0 – любая из (-;+). Возьмем произвольную последовательность {xn} такую, что xn→x0, n→. Соответствующая последовательность значений функции будет такой: f(x1)=С, f(x2)=С, … , f(xn)=С, … .
f(xn)→С=f(x0), при n→.
А это означает, что функция f(x) непрерывна в точке х0. Т.к. точка х0 – любая точка из промежутка (-;+). Следовательно, f(x) непрерывна в промежутке (-;+).
Или С=С-С=0.
2) f(x)=x, x(-;+)
Выберем произвольную точку х0(-;+). Возьмем произвольную последовательность {xn} такую, что xn→x0, n→. Соответствующая последовательность значений функции будет такой: f(x1)=x1, f(x2)=x2, … , f(xn)=xn, … .
f(xn)→x0=f(x0), при n→.
А это означает, что функция f(x) непрерывна в точке х0. Т.к. точка х0 – любая точка из промежутка (-;+). Следовательно, f(x)=х непрерывна в промежутке (-;+).
3) f(x)=xn, x(-;+), nN
Эта функция непрерывна в промежутке (-;+), т.к. f(x)=х∙х∙…∙х. Следовательно, f(x)=xn непрерывна в промежутке (-;+) как произведение конечного числа функций, непрерывных в этом промежутке.
4) f(x)=a0xn+a1xn-1+a2xn-2+…+an-1x+an, x(-;+), nN – целая рациональная функция, полином – непрерывна в промежутке (-;+) как сумма конечного числа функций, непрерывных в этом промежутке.
5)
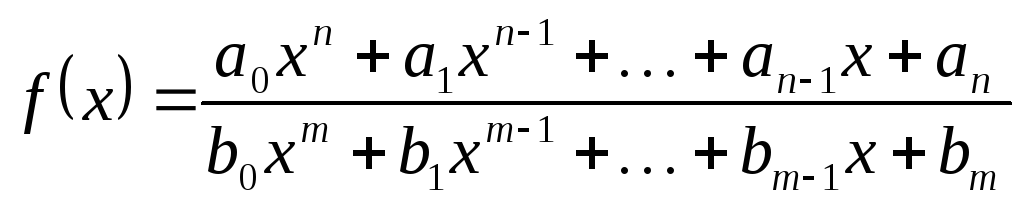 ,
nN,
mN
- дробная рациональная функция- непрерывна
в любой такой точке х0(-;+),
в которой знаменатель отличен от нуля,
т.е. f(x)
непрерывная в каждой точке своей области
определения.
,
nN,
mN
- дробная рациональная функция- непрерывна
в любой такой точке х0(-;+),
в которой знаменатель отличен от нуля,
т.е. f(x)
непрерывная в каждой точке своей области
определения.
6) Покажем, что функция f(x)=sin x непрерывна на всей своей области определения, т.е. на R=(-;+).
Возьмем х0.
![]() >0
>0
![]() δ=δ()
δ=δ()
![]() x:
|x-x0|<δ
x:
|x-x0|<δ
![]() |sin
x
- sin
x0|<
|sin
x
- sin
x0|<
Рассмотрим |sin
x
- sin
x0|=2![]() 2
2![]() 2
2![]() =|x-x0|
=|x-x0|
(т.к. |sin x| <|x-x0|)Т.о. |sin x - sin x0||x-x0|
Возьмем δ=,
тогда
![]() x:
|x-x0|<δ=
x:
|x-x0|<δ=
![]() |sin
x
- sin
x0|<.
Т.е.
|sin
x
- sin
x0|<.
Т.е.
![]()
7) Аналогично
доказывается непрерывность функции
f(x)=cos
x.
![]()
8)
![]() ,
,
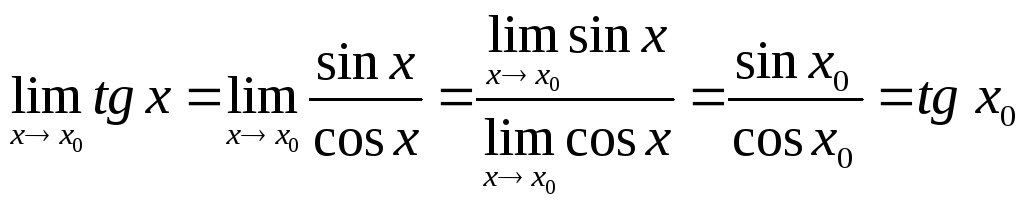
9) Аналогично
![]() ,
,
![]()
Все основные элементарные функции непрерывны на своей области определения.
Теорема 3. Пусть функция f(x) непрерывна в точке х0Х. Тогда существует окрестность V(x0) точки х0, на которой функция ограничена. Т.е.
![]() и
и
![]()
Доказательство. Т.к. f(x) непрерывна в точке х0, то
![]()
Возьмем =1 и оценим f(x)=f(x)-f(x0)+f(x0)f(x)-f(x0)+ f(x0)<1+f(x0)
Т.о. f(x)<1+f(x0), т.е. f(x) – ограничена. Ч.т.д.
Теорема 4. Пусть функция f(x) непрерывна в точке х0Х и f(x0)≠0. Тогда существует окрестность V(x0) точки х0, на которой
![]()
Причем, если
f(x0)>0,
![]() (xV(x0))
(xV(x0))
если f(x0)<0,
![]() (xV(x0))
(xV(x0))
