
- •§ 7. Свойства некоторых элементарных функций, их конформные отображения
- •Решение.
- •Решение.
- •Решение.
- •Решение.
- •Решение.
- •5. Показательная функция
- •Решение.
- •6. Тригонометрические и гиперболические функции
- •7. Функция Жуковского
- •§ 8. Интеграл от фкп п. 1. Определение, теорема существования
- •П. 2. Вычисление и свойства
- •Свойства
- •Решение.
- •Решение.
- •П. 3. Теорема Коши. Интегральная формула Коши
- •Следствия из теоремы Коши
- •Решение.
- •Решение.
- •Решение.
- •Решение.
Решение.
Контур L
:
![]() – уравнение окружности с центром в
начале координат и радиусом
– уравнение окружности с центром в
начале координат и радиусом
![]() .
D
– область внутри окружности (рис. 36).
.
D
– область внутри окружности (рис. 36).
Н айдем
особые точки подынтегральной функции
айдем
особые точки подынтегральной функции
![]() ,
т.е. точки, где знаменатель обращается
в нуль:
,
т.е. точки, где знаменатель обращается
в нуль:
![]()
![]()
![]()
![]()
![]() ,
,
![]() особые точки.
особые точки.
Данные точки не
лежат внутри контура интегрирования L
(рис. 35), т.е.
![]() ,
следовательно, по теореме Коши (формула
19 или по правилу 1 замечания),
,
следовательно, по теореме Коши (формула
19 или по правилу 1 замечания),
![]()
Пример . Вычислить
интеграл по заданному контуру:
![]() .
.
Решение.
![]()

 – уравнение
окружности с центром в точке z
= i
и радиусом 1. D1
– область внутри окружности (рис. 37).
– уравнение
окружности с центром в точке z
= i
и радиусом 1. D1
– область внутри окружности (рис. 37).
![]() ,
,
![]() особые точки подынтегральной функции
особые точки подынтегральной функции
![]() (нашли в примере 1). Из них точка
(нашли в примере 1). Из них точка
![]() ,
точка
,
точка
![]() .
.
Поэтому рассмотрим
многосвязную область D,
ограниченную окружностью
![]() и внутренним контуром
и внутренним контуром
![]() (рис. 38).
(рис. 38).
Тогда в этой области
функция
![]() аналитическая, и по следствию 1 (теореме
Коши для многосвязной области (формула
(21/))
можем записать, что
аналитическая, и по следствию 1 (теореме
Коши для многосвязной области (формула
(21/))
можем записать, что
![]() ,
т.е.
,
т.е.
![]() =
=
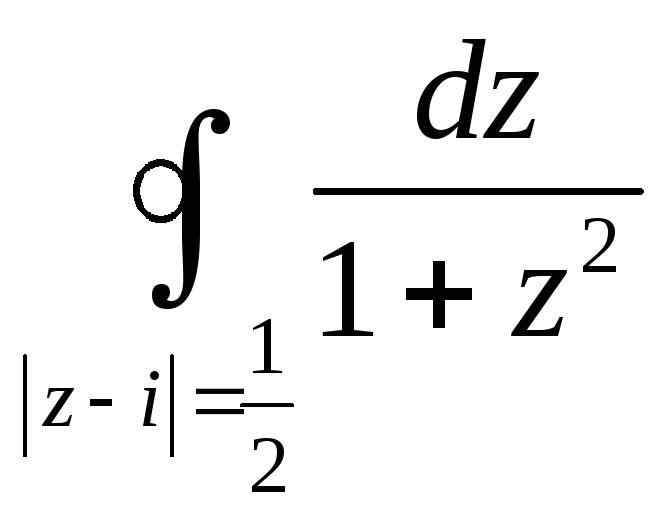 .
.
Данный интеграл
вычислим при помощи интегральной формулы
Коши :
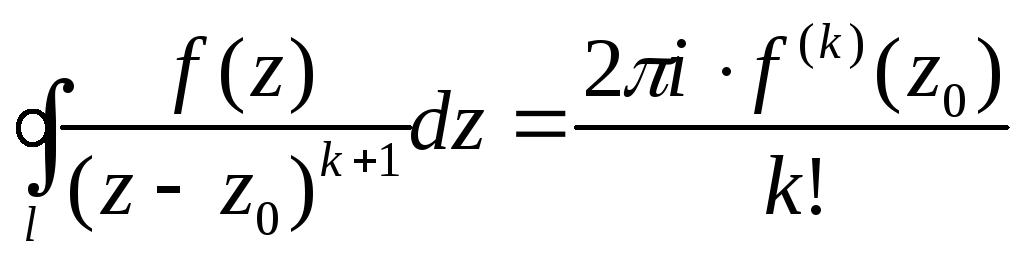 .
Для этого выделим в знаменателе особую
точку:
.
Для этого выделим в знаменателе особую
точку:
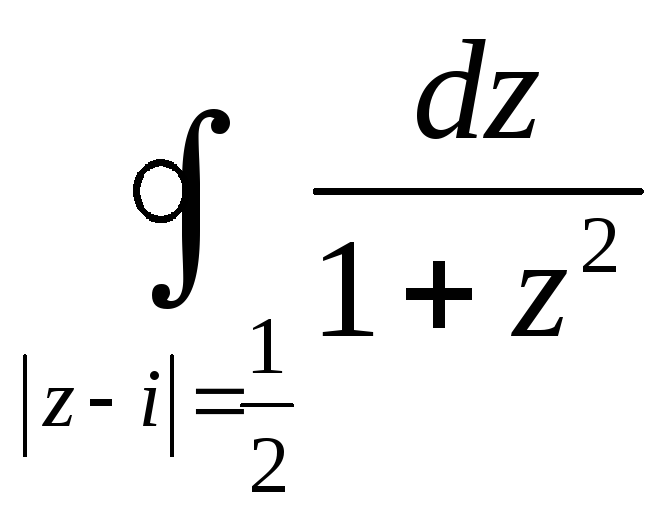 =
=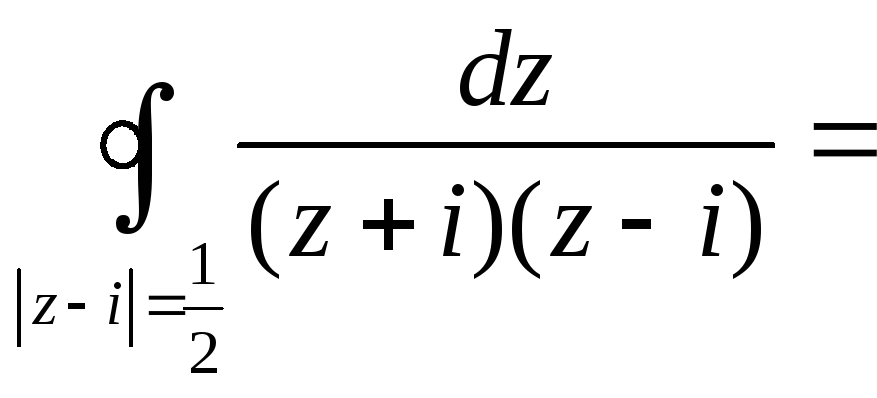
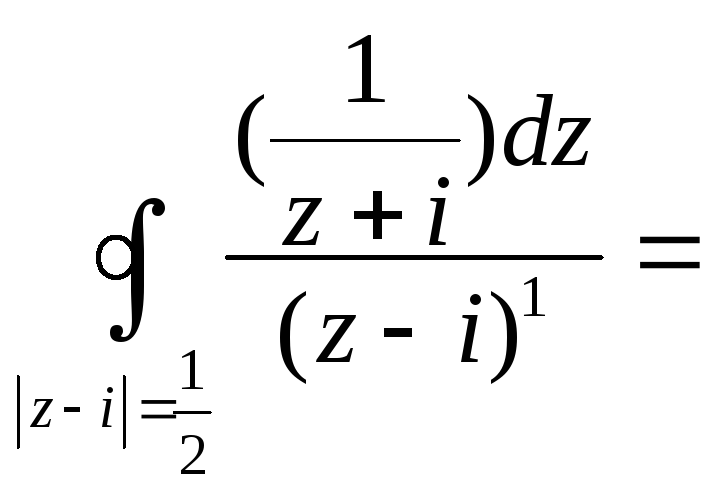 (k
= 0,
(k
= 0,
![]() )
=
)
=
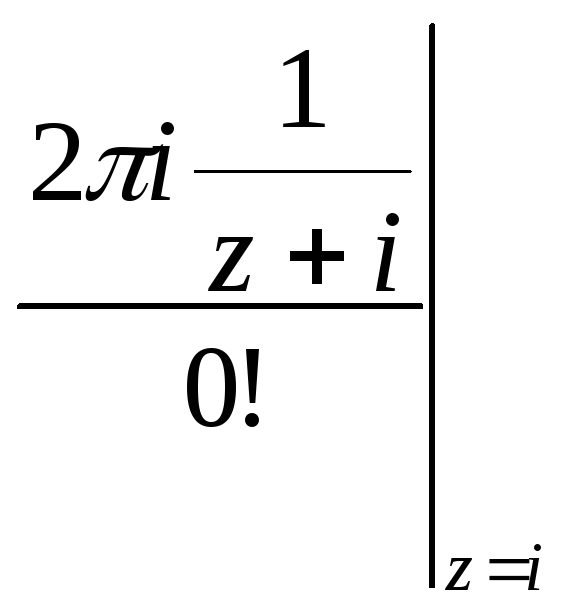 =
=
![]()
Замечание. Данный пример можно решить, используя следствие к теореме 12, не выделяя внутреннюю область, ограниченную контуром l или по правилу 2 замечания.

Пример . Вычислить
интеграл по заданному контуру:
![]() .
.
Решение.
![]() – уравнение
окружности с центром в точке z
= i
и радиусом 3. D1
– область внутри окружности (рис. 39).
– уравнение
окружности с центром в точке z
= i
и радиусом 3. D1
– область внутри окружности (рис. 39).

![]() ,
,
![]() особые точки функции
особые точки функции
![]() (нашли в примере 1). Они обе лежат внутри
контура. Поэтому рассмотрим многосвязную
область D,
ограниченную окружностью
(нашли в примере 1). Они обе лежат внутри
контура. Поэтому рассмотрим многосвязную
область D,
ограниченную окружностью
![]() и двумя внутренними контурами
и двумя внутренними контурами
![]() и
и
![]() (рис. 40).
(рис. 40).
Тогда в этой области
функция
![]() аналитическая, и по следствию 1 (теореме
Коши для многосвязной области (формула
(21/))
можем записать, что
аналитическая, и по следствию 1 (теореме
Коши для многосвязной области (формула
(21/))
можем записать, что
![]() ,
т.е.
,
т.е.
![]() =
=
![]()
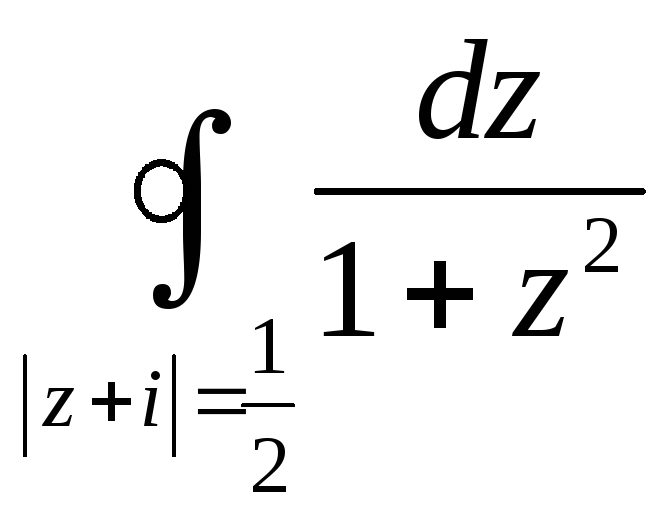 =
(выделим в знаменателях особые точки)
= =
=
(выделим в знаменателях особые точки)
= =![]() +
+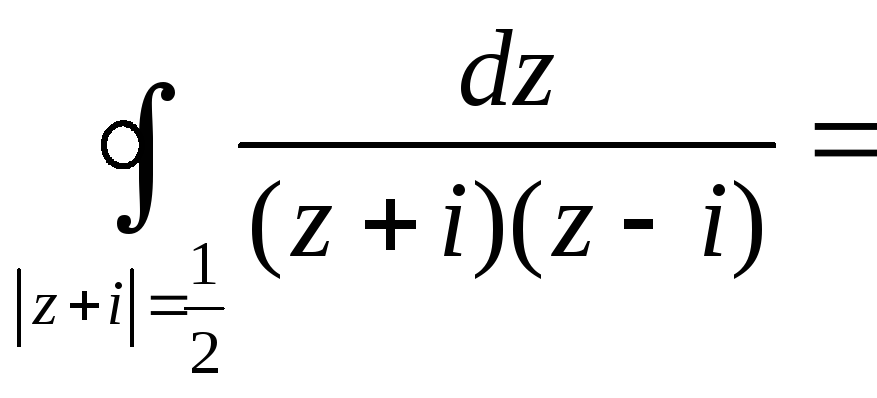
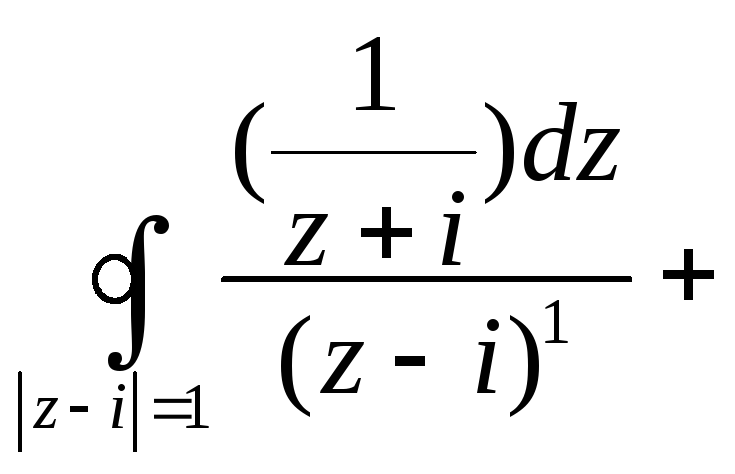
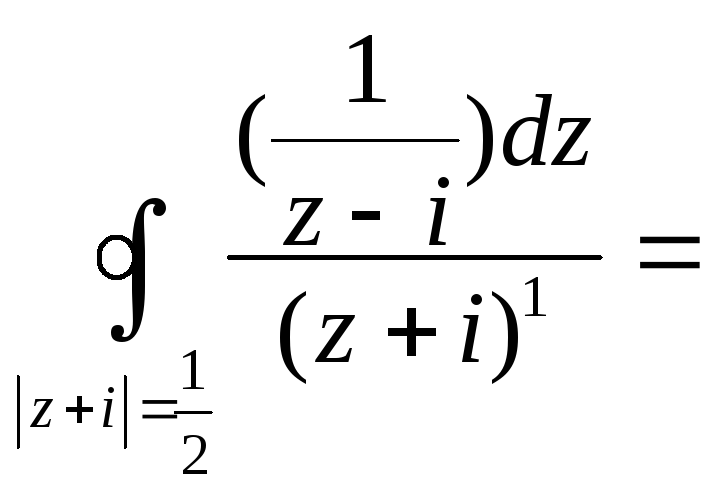
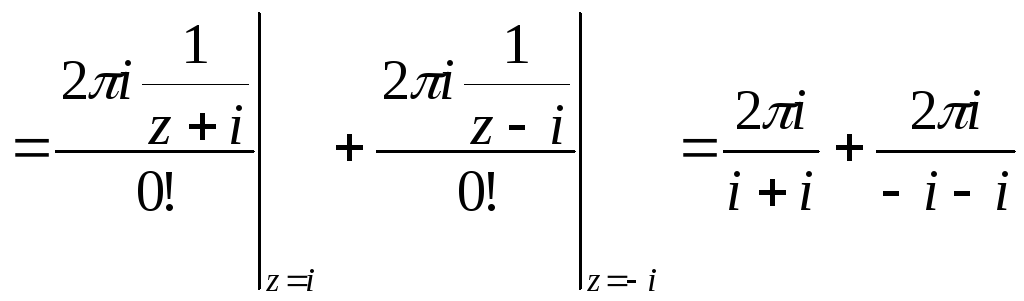 =
=
![]() .
.
Пример . Вычислить
интеграл по заданному контуру:
![]() .
.
Решение.
![]()
 – уравнение
окружности с центром в точке z
= –i
и радиусом 2. D1
– область внутри окружности (рис. 41).
– уравнение
окружности с центром в точке z
= –i
и радиусом 2. D1
– область внутри окружности (рис. 41).
Найдем особые
точки:
![]()
![]()
![]() ,
,
![]() – особые точки, причем
– особые точки, причем
![]() имеет кратность равную 2.
имеет кратность равную 2.
Знаменатель
обращается в нуль внутри контура в
особой точке
![]() вторая особая точка
вторая особая точка
![]() .
Тогда в области D
функция
.
Тогда в области D
функция
![]() аналитическая, за исключением нуля, и
по следствию к теореме 12 или правилу 3
замечанию к нему, можем записать, что
аналитическая, за исключением нуля, и
по следствию к теореме 12 или правилу 3
замечанию к нему, можем записать, что
![]() =
=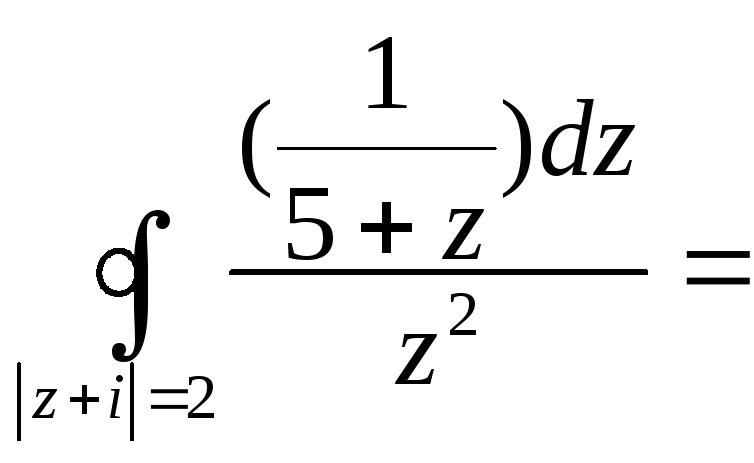
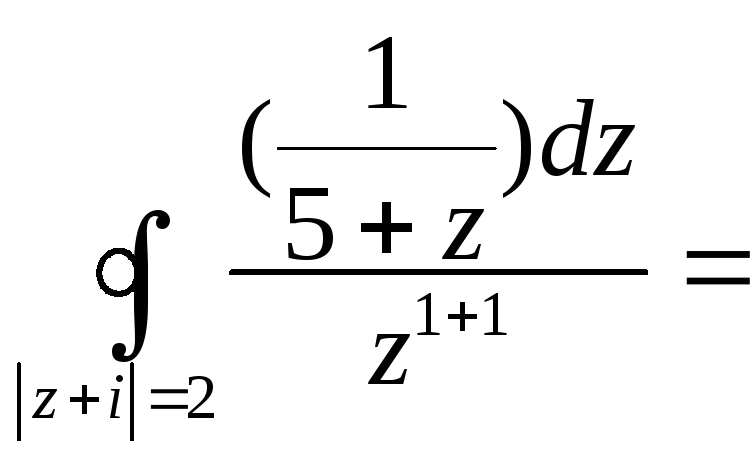 (k
= 1,
(k
= 1,
![]() )
=
)
=
=
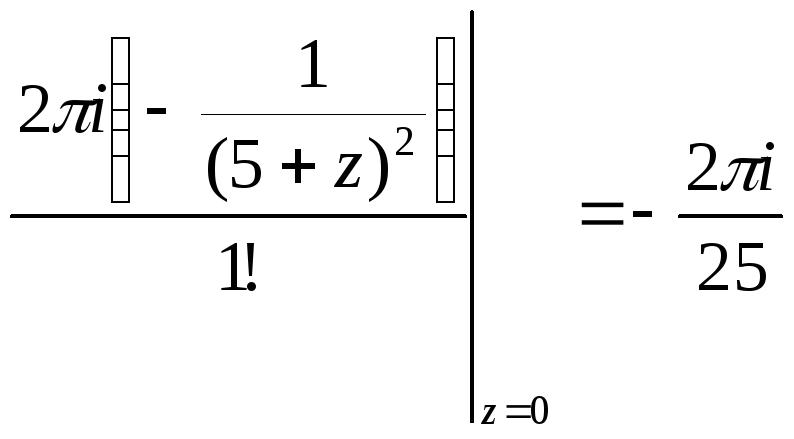 .
.
