§23. Предельные случаи теорем Паскаля и Брианшона

Рассмотрим предельные (частные) случаи теорем Паскаля и Брианшона.

Представим себе, что точки определяющие какую-нибудь сторону вписанного шестивершинника, сливаются, тогда эта сторона превращается в касательную и получается фигура, изображенная на следующем рисунке

Рис. 21

Теорема. Касательная к линии второго порядка, проведенная в одной из вершин вписанного пятивершинника, пересекается со стороной, противоположной этой вершине, в точке, которая лежит на прямой, проходящей через точки пересечения остальных пар несмежных сторон этого пятивершинника.

Двойственную этому предельному случаю теорему Брианшона получим, полагая, что две смежные стороны описанного шестисторонника сливаются в одну, а общая их вершина превращается в точку прикосновения.

Теорема. Прямая, соединяющая точку касания одной из сторон описанного пятисторонника с противоположной вершиной, проходит через общую точку прямых, соединяющих остальные две пары несмежных вершин этого пятисторонника.

Рис. 22

Задача 49. Овальная кривая второго порядка задана четырьмя точками и касательной в одной из них.

а) Построить касательную к кривой в одной из данных точек;

б) Построить еще одну точку кривой.

Решение.

а) Пусть заданы точки ,, ,, и прямая – касательная к кривой в точке . Построим касательную к кривой в точке .Примем точки и за центры пучков и , порождающих кривую ( следствие теоремы Штейнера). В проективном отображении , которое переводит прямые , , соответственно в прямые , , , касательной к кривой в точке является прямая . Задача сводится к построению образа прямой в заданном проективном отображении . Для этого построим точку – центр перспективного отображения . Находим далее , . Прямая – искомая касательная.

б) Возьмем произвольную прямую и найдем . Тогда по теореме Штейнера .

Рис. 23

Задача 50. Зная пять точек кривой второго порядка, построить касательную в одной из них.

Решение. Задача решается с помощью теоремы Паскаля для вписанного пятивершинника. Пусть отрезки, соединяющие данные точки, помечены числами , , , , , а назначенная точка – числом . Тогда, построив сначала точки , , а затем точку , соединяем точку с точкой , получая искомую касательную.

Рис. 24

Задача 51. Зная пять касательных кривой второго порядка, построить точку прикосновения одной из них.

Решение. Задачу решаем при помощи теоремы Брианшона для описанного пятисторонника. Пусть точки пересечения данных касательных помечены числами , , , , . Тогда, соединяя прямыми точки , и точки , , находим точку пересечения этих прямых. Прямая, соединяющая эту точку с точкой , пересечением с прямой , определит на ней искомую точку касания.

Рис. 25

Связь между проективными и аффинными координатами. Геометрия аффинной плоскости с проективной точки зрения.

Прежде всего рассмотрим проективную прямую P¹, вложенную в расширенную плоскость.

Обсудим отличие аффинной прямой от проективной. Ясно, что проективная прямая имеет на одну точку больше, чем аффинная. Напомним, что координатой точки M аффинной прямой в репере (A, e) называется такое число x, что = xe.

Лемма. Пусть на расширенной прямой выбраны репер R = (A, B_∞, E), где B_∞ - несобственная точка, и собственная точка M, имеющая в репере R координаты (x¹, x²). Тогда точка M в аффинном репере (A, ) аффинной прямой d имеет координату .

Доказательство. Возьмем собственную точку O расширенной плоскости, не лежащую на прямой . Пусть x - аффинная координата точки M в репере (A, ), то есть = x.

П усть вектор параллелен прямой d и + = . Система векторов , , согласована и порождает точки проективного репера R = (A, B_∞, E), заметим, что = . Поскольку = x, то = + x. Вектор порождает точку M, поэтому числа (1,x) являются координатами точки M в репере R. По условию леммы (x¹, x²) также координаты точки M, следовательно (1,x) и (x¹, x²) пропорциональны, т.е. x= , что и требовалось доказать.

Обобщим конструкцию на случай репера, заданного на расширенной плоскости . Пусть на задан репер R = (A, Х_∞, Y_∞, E), где точки A и E - собственные, а X_∞, Y_∞ - бесконечно удаленные.

Пусть E₃ = (AX_∞) ∩ (Y_∞ E), E₂ = (A Y_∞) ∩ (X_∞ E). Если M_∞ есть какая-либо несобственная точка расширенной плоскости, то она принадлежит бесконечно удаленной координатной прямой (X_∞ Y_∞), и имеет координаты (0, x², x³). Если N(y¹, y², y³) – собственная точка, то y¹ ≠ 0. Положим e₁ = и e₂ = , тогда на аффинной плоскости = e₁ + e₂.

Рассмотрим аффинный репер R₀ = (A, e₁, e₂), пусть в этом репере точка N имеет координаты (x, y). Используя результат леммы, имеем x = , y = .

Рассмотрим множество H всех проективных преобразований расширенной плоскости, переводящих несобственную прямую (Х_∞ Y_∞) в себя, H есть подгруппа группы всех проективных преобразований плоскости. Пусть fH, запишем аналитическое выражение преобразования f в репере  = (A, Х_∞, У_∞, E):

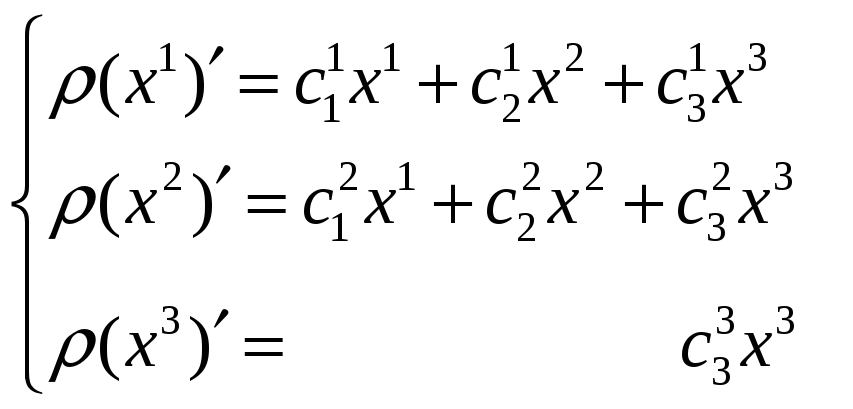(1)

Бесконечно удаленная прямая имеет уравнение x³=0 и при преобразовании f переходит в себя, следовательно, = 0, = 0. В формулах (1) ρ ≠ 0, ≠ 0, ≠ 0.

Разделив почленно первое и второе равенства в (1) на третье, получаем

, где =, i, j = 1,2, ≠ 0.

Группа аффинных преобразований аффинной плоскости изоморфна H, таким образом, аффинную геометрию на плоскости можно рассматривать как геометрию, изучающую свойства фигур, инвариантных относительно группы H.