3. Випадкові величини

3.1. Випадкові величини. Функції розподілу. Числові характеристики випадкових величин.

Випадковою величиною зветься дійсна функція , яка визначена на множині елементарних подій і така, що при довільному дійсному множина тих , для яких належить алгебрі подій для даного експерименту. Функція дійсної змінної х, , яка визначається формулою

, (3.1)

зветься функцією розподілу випадкової величини та має наступні властивості:

1) ;

2) ;

3) , якщо ;

4) ; .

Якщо - дискретна випадкова величина, яка приймає значення , , ... з ймовірностями , , ..., то функція розподілу має вигляд

, (3.2)

де сумуються ймовірності тих значень , які менші . Якщо - неперервна випадкова величина із щільністю розподілу , то функція розподілу має вигляд

. (3.3)

Щільність розподілу ймовірностей має такі властивості:

1) ;

2) ;

3) ;

4) .

Неперервна випадкова величина задається або функцією розподілу , або щільністю ймовірностей . Рядом (або законом) розподілу дискретної випадкової величини називають таблицю вигляду

				...
				...

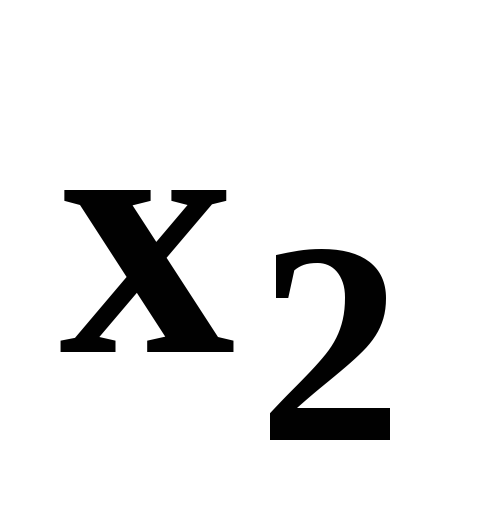
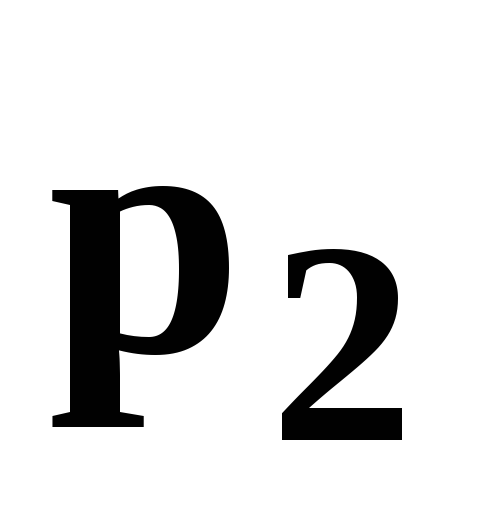
Тут - можливі значення ;

, .

Випадкові величини, крім законів розподілу, можуть також описуватися числовими характеристиками, серед яких розрізняють характеристики положення (математичне сподівання, мода, медіана та інші) та характеристики розсіювання (дисперсія, середнє квадратичне відхилення, різні моменти розподілу вищі першого та інші).

Математичним сподіванням називається дійсне число, яке визначається в залежності від типу випадкової величини формулою

якщо - дискретна випадкова величина; (3.4)

якщо - неперервна випадкова величина. (3.5)

Основні властивості математичного сподівання:

1) , де ;

2) , де ;

3) , де - незалежні випадкові величини;

4) .

Модою неперервної випадкової величини називається число , яке визначається як точка максимуму щільності розподілу ймовірностей .

Мода дискретної випадкової величини визначається як таке можливе значення , для якого .

Медіаною неперервної випадкової величини називається число , яке задовольняє умові: , або .

Дисперсією випадкової величини називається число , яке визначається формулами:

, якщо - дискретна випадкова величина; (3.6)

, якщо - неперервна випадкова величина. (3.7)

Основні властивості дисперсії:

1) ;

2) , де ;

3) , де ;

4) _;

₅₎ .

Невід’ємне число називається середньоквадратичним відхиленням випадкової величини . Воно має розмірність випадкової величини та визначає деякий стандартний інтервал розсіювання.

Початковим моментом -го порядку розподілу випадкової величини називається дійсне число

, якщо - дискретна випадкова величина; (3.8)

, якщо - неперервна випадкова величина. (3.9)

Центральним моментом -го порядку розподілу випадкової величини називається дійсне число , яке визначається формулою

, якщо - дискретна випадкова величина; (3.10)

, якщо - неперервна випадкова величина. (3.11)

Центральні моменти виражаються через початкові моменти за формулами:

; (3.12)

; (3.13)

. (3.14)

Відмітимо ще дві важливі характеристики розподілу, зв’язані з моментами вищих порядків:

- коефіцієнт асиметрії або скошеності розподілу; (3.15)

- коефіцієнт ексцесу або “гостровершинність” розподілу. (3.16)