
- •Тема 1 числові ряди 5
- •Тема 2 функціональні ряди 30
- •Тема 3 ряди фур'є 67
- •Передмова
- •Тема 1 числові ряди
- •1.1 Поняття числового ряду. Збіжні і розбіжні ряди
- •1.2 Найпростіші властивості збіжних рядів
- •Доведення
- •Доведення
- •Доведення
- •1.3 Додатні ряди. Ознаки збіжності
- •Доведення
- •Розв’язування
- •Доведення
- •Розв’язування
- •Розв’язування
- •Доведення
- •Розв’язування
- •Розв’язування
- •Доведення
- •Розв’язування
- •Доведення
- •Доведення
- •Розв’язування
- •Розв’язування
- •Доведення
- •Доведення
- •Розв’язування
- •1.4 Ряди з довільними членами. Знакозмінні ряди
- •Доведення
- •Розв’язування
- •Доведення
- •Розв’язування
- •Доведення
- •Розв’язування
- •1.5 Властивості абсолютно збіжних рядів
- •1.6 Розв’язування задач із використанням ознак збіжності рядів
- •Питання для самоперевірки
- •Завдання для самостійної роботи
- •Тема 2 функціональні ряди
- •2.1 Поняття функціонального ряду і області його збіжності. Поняття рівномірної збіжності функціонального ряду. Властивості рівномірно збіжних рядів
- •Розв’язування
- •Доведення
- •Властивості рівномірно збіжних рядів
- •2.2 Степеневі ряди. Теорема Абеля
- •Розв’язування
- •Розв’язування
- •Доведення
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •2.3 Властивості суми степеневого ряду
- •Доведення
- •Доведення
- •Доведення
- •Доведення
- •Розв’язування
- •2.4 Формула і ряд Тейлора
- •Доведення
- •Доведення
- •2.5 Розвинення елементарних функцій в ряд Тейлора
- •2.6 Застосування степеневих рядів
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •2.7 Приклади розв’язування типович задач
- •Розв’язування
- •Питання для самоперевірки
- •Завдання для самостійної роботи
- •Тема 3 ряди фур'є
- •3.1 Ортогональна система функцій. Ряд Фур'є
- •Доведення
- •Розвязування
- •Розв’язування
- •3.2 Ряди Фур'є для парних і непарних функцій
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •3.3 Ряд Фур'є для функції з довільним періодом 2l
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •3.4 Ряд Фур'є в комплексній формі
- •Розв’язування
- •Розв’язування
- •3.5 Узагальнений ряд Фур'є
- •3.6 Інтеграл Фур'є
- •Розв’язування
- •Розв’язування
- •3.7 Комплексна форма інтеграла Фур’є
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •3.8 Приклади розв’язування типових задач
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •Питання для самоперевірки
- •Завдання для самостійної роботи
- •Література
- •Додаток а
- •Додаток в
- •Порядок виконання завдання
- •21021, М. Вінниця, Хмельницьке шосе, 95, внту
- •21021, М. Вінниця, Хмельницьке шосе, 95, внту
2.5 Розвинення елементарних функцій в ряд Тейлора
1.
Функція
![]() .
.
Оскільки
дана функція в кожній точці
![]() числової осі має похідну будь-якого
порядку
числової осі має похідну будь-якого
порядку
![]() ,
то
,
то
![]() і вона породжує степеневий ряд
і вона породжує степеневий ряд
![]()
Цей ряд
збіжний при будь-якому
![]() саме до функції
саме до функції
![]() ,
бо на будь-якому відрізку
,
бо на будь-якому відрізку
![]() для кожному натурального
для кожному натурального
![]() :
:
![]() .
.
Отже,
![]() . (2.17)
. (2.17)
2.
Функція
![]() .
.
Ця
функція при будь-якому
![]() має всі похідні, причому
має всі похідні, причому
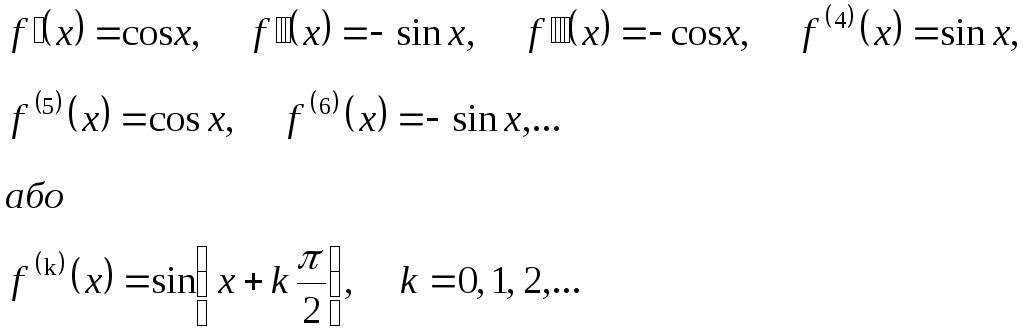
Тоді
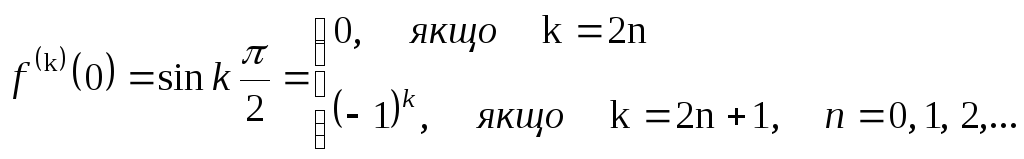
Отже ця функція породжує степеневий ряд
![]()
Цей ряд
збіжний при будь-якому
![]() саме
до функції
саме
до функції
![]() ,
бо
при довільному
,
бо
при довільному
![]() і
для кожного натурального
і
для кожного натурального
![]() :
:
![]() .
.
Таким
чином при
![]() маємо
маємо
![]() (2.18)
(2.18)
3.
Функція
![]() .
.
Рівність
![]() (2.19)
(2.19)
доводиться аналогічно рівності (2.18), або почленним диференціюванням останньої.
4.
Функція
![]() .
.
Знайдемо ряд Тейлора для цієї функції, виходячи з очевидної рівності
![]()
яка
виконується при
![]() (бо праворуч маємо геометричну прогресію
зі знаменником
(бо праворуч маємо геометричну прогресію
зі знаменником
![]() ).
Використовуючи
можливість почленного інтегрування
степеневого ряду, дістанемо
).
Використовуючи
можливість почленного інтегрування
степеневого ряду, дістанемо
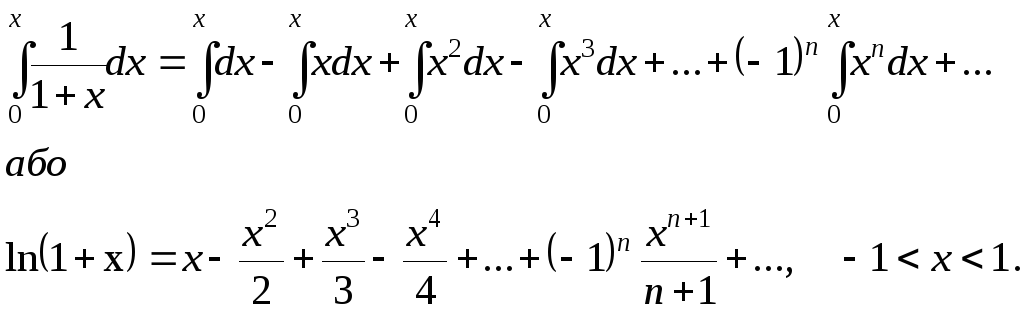
Відмітимо,
що шляхом безпосереднього дослідження
залишкового члена формули Тейлора можна
переконатися у справедливості останньої
рівності і при
![]() .
.
Отже,
![]() (2.20)
(2.20)
5.
Функція
![]() .
.
Інтегруючи рівність
![]()
справедливу
при
![]() (геометрична професія зі знаменником
(геометрична професія зі знаменником
![]() ),
дістанемо
),
дістанемо
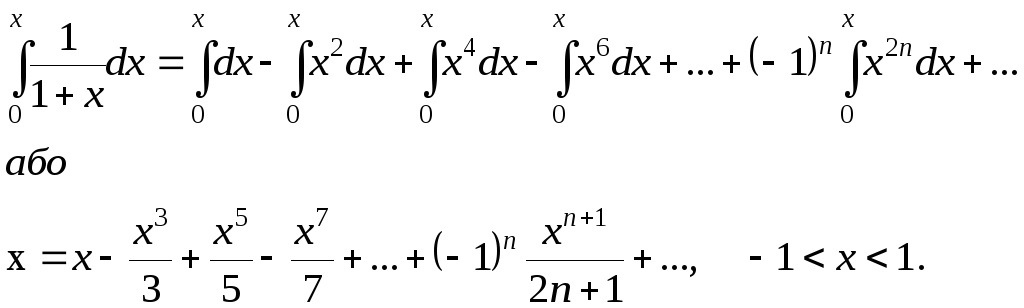
Як і в
попередньому прикладі можна довести,
що остання рівність виконується при
![]() .
.
Отже,
![]() (2.21)
(2.21)
6.
Функція
![]() ,
де
,
де
![]() - довільне дійсне число.
- довільне дійсне число.
Для цієї функції маємо
![]()
тому
функція
![]() породжує степеневий ряд (
породжує степеневий ряд (![]() )
)
![]()
![]()
і його називають біноміальним рядом.
Оскільки за ознакою Д’Аламбера
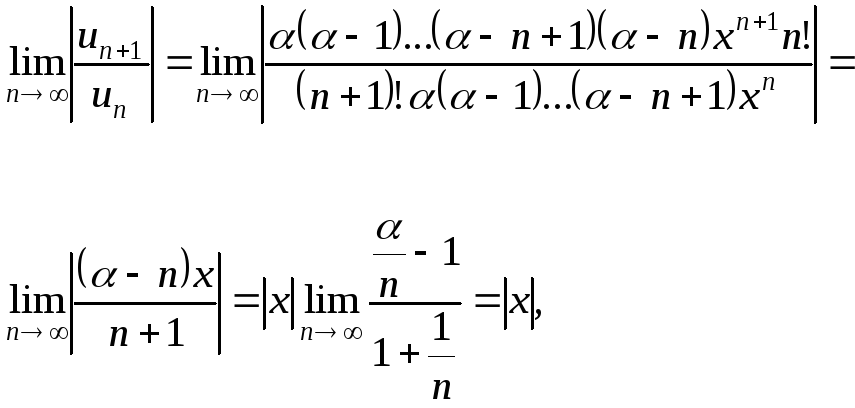
то
біноміальний ряд збіжний при
![]() і розбіжний при
і розбіжний при![]() .
.
Доведемо,
що при
![]() цей ряд збіжний саме до функції
цей ряд збіжний саме до функції
![]() .
Справді, нехай при
.
Справді, нехай при
![]()
![]() (2.22)
(2.22)
тоді
![]() (2.23)
(2.23)
![]() (2.24)
(2.24)
Почленним додаванням рівностей (2.23) і (2.24) з урахуванням (2.22) маємо
![]()
що можна записати у вигляді
![]()
Тому
![]() (
(![]() -
стала),
звідки
-
стала),
звідки
![]() .
Але
.
Але
![]() .
Підставляючи це значення у формулу
(2.22), дістанемо рівність
.
Підставляючи це значення у формулу
(2.22), дістанемо рівність
![]() (2.25)
(2.25)
справедливу
для інтервалу
![]() .
Ця рівність узагальнює відому формулу
бінома Ньютона на випадок будь-якого
дійсного показника.
.
Ця рівність узагальнює відому формулу
бінома Ньютона на випадок будь-якого
дійсного показника.
Зауваження.
Можна
довести що при
![]() рівність
(2.25) справджується на відрізку
рівність
(2.25) справджується на відрізку
![]() ,
при
,
при
![]() – на півінтервалі
– на півінтервалі
![]() ,
при
,
при
![]() на
інтервалі
на
інтервалі
![]() .
.
Зазначимо,
що експоненціальна функція
![]() та
тригонометричні функції
та
тригонометричні функції
![]() пов'язані між собою формулами Ейлера.
Виведемо ці формули. У ряді (2.17) формально
замість
пов'язані між собою формулами Ейлера.
Виведемо ці формули. У ряді (2.17) формально
замість
![]() приймемо
приймемо
![]() (уявна
одиниця). Матимемо
(уявна
одиниця). Матимемо
![]()
![]() .
(2.26)
.
(2.26)
У круглих
дужках цієї рівності містяться ряди,
які зображають, відповідно, функції
![]() .
Тому рівність можна записати так:
.
Тому рівність можна записати так:
![]() .
(2.27)
.
(2.27)
Якщо в
ряді (2.17) замість
![]() формально
прийняти
формально
прийняти
![]() ,
то дістанемо таку рівність:
,
то дістанемо таку рівність:
![]() .
(2.28)
.
(2.28)
Тоді з формул (2.27) і (2.28) знаходимо
![]() .
(2.29)
.
(2.29)
Формули (2.27) і (2.28) називають формулами Ейлера.
2.6 Застосування степеневих рядів
1. Наближене обчислення значень функцій
Нехай
функція
![]() в деякому проміжку розвивається в
степеневий ряд
в деякому проміжку розвивається в
степеневий ряд
![]()
Тоді
легко наближено обчислити значення
функції
![]()
![]() шляхом
заміни її скінченним числом перших
членів цього розкладу.
шляхом
заміни її скінченним числом перших
членів цього розкладу.
Чим
менше
![]() ,
тим менше членів береться для обчислення
,
тим менше членів береться для обчислення
![]() з бажаною точністю. Якщо х
дуже мале, то достатньо обмежитись
тільки двома першими членами, відкинувши
всі останні. Таким чином, дістаємо дуже
просту формулу для
з бажаною точністю. Якщо х
дуже мале, то достатньо обмежитись
тільки двома першими членами, відкинувши
всі останні. Таким чином, дістаємо дуже
просту формулу для
![]()
![]() ,
яка
при малих
,
яка
при малих
![]() цілком може замінити часто досить
складний точний вираз для
цілком може замінити часто досить
складний точний вираз для
![]() .
.
а) Обчислення значень тригонометричних функцій
Степеневі
ряди (2.18) і (2.19) можна використати для
обчислення значень тригонометричних
функцій
![]() і
і
![]() .
Оскільки
ряди знакозмінні, то залишок ряду не
перевищує за абсолютною величиною
першого з відкинутих членів. Для
.
Оскільки
ряди знакозмінні, то залишок ряду не
перевищує за абсолютною величиною
першого з відкинутих членів. Для
![]() матимемо
матимемо
![]() , (2.30)
, (2.30)
![]() .
(2.31)
.
(2.31)
Користуючись
формулами (2.30) і (2.31), можна підібрати
найменше число
![]() таке,
щоб дістати значення
таке,
щоб дістати значення
![]() і
і
![]() з наперед заданою точністю.
з наперед заданою точністю.
Відмітимо,
що ряди (2.18) і (2.19) швидше збігаються при
малих значеннях
![]() .
Доцільно обчислювати за допомогою цих
рядів значення синуса і косинуса для
кутів від
.
Доцільно обчислювати за допомогою цих
рядів значення синуса і косинуса для
кутів від
![]() до
до
![]() .
Значення ж цих функцій для кутів від
.
Значення ж цих функцій для кутів від
![]() до
до
![]() легко обчислити, якщо скористатись
формулами:
легко обчислити, якщо скористатись
формулами:
![]()
![]()
![]()
![]() .
.
А значення
функцій
![]() та
та
![]() для кутів від
для кутів від
![]() до
до
![]() знаходяться за допомогою формул зведення.
знаходяться за допомогою формул зведення.
Зауваження. Для обчислення кути, виражені в градусах потрібно перевести в радіани.
Приклад
2.12
Обчислити
![]() з точністю до
з точністю до
![]() .
.
