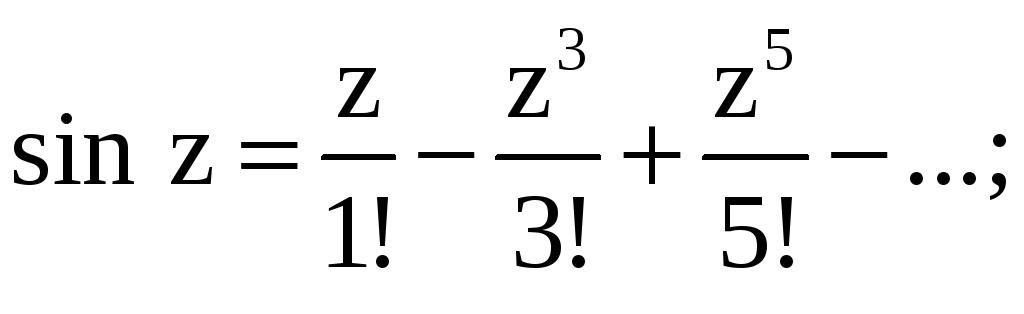Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

«Омский государственный технический университет»

Теория функций комплексного переменного

Методические указания для дистанционного обучения

студентов 1-2 курсов

экономических и технических специальностей

Омск-2005

Составители: Веснина Алла Александровна, доцент,

Хаустова Нина Михайловна, ст. преподаватель.

Печатается по решению редакционно-издательского отдела Омского государственного технического университета.

КОМПЛЕКСНЫЕ ЧИСЛА И ДЕЙСТВИЯ НАД НИМИ

Комплексными числами называются числа вида , где – действительные числа, – действительная часть, – мнимая часть комплексного числа.

По определению, два комплексных числа: и – равны тогда и только тогда, когда и .

Комплексное число называется сопряженным комплексному числу , если . Другими словами, если , то .

Всякому комплексному числу можно поставить в соответствие единственную точку плоскости и обратно, всякую точку плоскости можно рассматривать как геометрический образ единственного комплексного числа .

y М 0 х Рисунок 1

Для сокращения вместо “точка, соответствующая комплексному числу ”, говорят просто “точка ”. При этом множество всех действительных чисел изображается точками оси абсцисс, которая поэтому называется действительной осью, множество чисто мнимых чисел точками оси ординат, называемой мнимой осью. Заметим, что одна точка мнимой оси, а именно начало коорди-

нат, изображает действительное число нуль. Плоскость, точки которой изображают комплексные числа, называется комплексной плоскостью.

В некоторых случаях удобно считать геометрическим изображением числа радиус-вектор точки – .

y 0 z3 5 x -2 z2 -5 z1 Рисунок 2

Пример 1. Построить точки , , . В дальнейшем, наряду с представлением комплексных чисел в декартовых координатах, полезно иметь их представление в обобщенных полярных координатах. Рассмотрим число , которому на плоскости соответствует точка . Ее координаты в полярной системе координат .

y M(x; y) ρ φ 0 x Рисунок 3

Тогда . . Полярный радиус называется модулем комплексного числа и обозначается .

Полярный угол называется аргументом комплексного числа и обозначается . Тогда

.

Эта форма называется тригонометрической формой комплексного числа.

Модуль комплексного числа определяется однозначно: .

Аргумент комплексного числа определяется с точностью до слагаемого, кратного . Главным значением аргумента называется значение, заключенное в интервале . Обозначается оно . Таким образом, .

Очевидно, .

Главное значение аргумента определяется однозначно.

Так как ,

Тригонометрическая форма комплексного числа будет иметь вид

.

Пример 2. Написать в тригонометрической форме комплексное число .

y z 1 -1 0 x Рисунок 4

Решение. .

Пусть . Используя формулу Эйлера , получаем так называемую показательную форму записи комплексного числа:

.

Пример 3. Представить в показательной форме комплексное число .

y -1 0 x z -1 Рисунок 5

Решение

Пример 4. Вычислить .

Решение. По формуле Эйлера .

АЛГЕБРАИЧЕСКИЕ ДЕЙСТВИЯ НАД КОМПЛЕКСНЫМИ ЧИСЛАМ

Сложение и умножение комплексных чисел производится по правилам сложения и умножения алгебраических многочленов с учетом . При записи результата следует отделить действительную часть от мнимой, т. е. собрать отдельно члены, содержащие множитель , и члены, не содержащие множитель :

В частности, . Операции сложения и вычитания сводятся к сложе- нию и вычитанию векторов, изображающих эти числа. Отсюда расстояние между точками .

y z1 z1+z2 z2 z1-z2 x Рисунок 6

Пример 5. – уравнение окружности с центром в точке и радиусом равным . Деление на комплексное число, отличное от нуля, определяется как действие, обратное умноже- нию. Для представления частного в виде следует провести простые преобразования, показанные на следующем примере.

Пример 6. .

Для модуля и аргумента произведения и частного справедливы следующие утверждения:

1.

Пример 7. Найти модуль и аргумент произведения .

Решение. .

Таким образом, умножение на соответствует повороту вектора на угол ;

2. .

Пусть .

Тогда .

Можно доказать методом полной математической индукции, что для любого целого (формула Муавра). Формула справедлива и для целых отрицательных .

Пример 8. Вычислить .

y 0 x -1 z Рисунок 7

Решение ,

,

.

Корнем -й степени из комплексного числа называется такое число , для которого .

Используя формулу Муавра, получим

Для других значений аргументы будут отличаться от полученных на число кратное , и, следовательно, получатся значения корня, совпадающие с рассмотренными. Итак, корень -й степени из комплексного числа имеет различных значений.

Пример 9. Найти все значения и построить их.

y φ x Рисунок 8

Решение. , , ,

,

,

.

ПОНЯТИЕ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО.

ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ

Говорят, что на множестве точек плоскости задана функция , если указан закон, по которому каждой точке из ставится в соответствие определенная точка или совокупность точек .

В первом случае функция называется однозначной, во втором – многозначной. В дальнейшем, если не будет оговорено противное, под функцией будем понимать однозначную функцию.

Если положить и , то задание функции комплексного переменного будет равносильным заданию двух функций двух действительных переменных: .

Функции комплексного переменного определяются как суммы следующих рядов, сходящихся на всей комплексной плоскости:

На действительной оси эти функции совпадают с соответствующими элементарными функциями действительного переменного.

Для функции комплексного переменного справедлива формула Эйлера:

.

Из этой формулы следует, что

Остаются справедливыми при комплексных значениях аргумента все тригонометрические тождества.

Основное свойство показательной функции также сохраняется. В частности,

Функции ( – целое положительное число), определяются как обратные функции по отношению к

и являются многозначными функциями.

Можно показать, что

В этом выражении при каждом фиксированном получаем однозначные функции, которые называются ветвями, называется главной ветвью функции .

;

;

.

Степень с комплексным основанием и комплексным показателем определяется равенством

.

Пример 1. Вычислить значения функций:

а) в точке .

Решение .

б) в точке .

Решение

Или, учитывая, что , получим

в) в точке .

Решение

Пример 2. Вычислить .

Решение

Условимся откладывать значения на одной комплексной плоскости, а значения – на другой. Тогда однозначную функцию комплексного переменного можно рассматривать как отображение множества плоскости на множество плоскости . Если при этом двум различным точкам всегда соответствуют различные точки , то такое отображение называется взаимно однозначным или однолистным в .

Пример 3. При отображении найти образ линии .

Решение. Так как , исключим из системы:

где – уравнение линии в плоскости .

Найдем искомую зависимость, связывающую и .

Преобразуя уравнение , получим

.

Таким образом, окружность в плоскости отображается в окружность в плоскости .

Пример 4. При отображении найти образ полярной сетки полуплоскости .

Решение

1. Найдем образы полуокружностей (рис. 8):

Образы-окружности с удаленной точкой .

y Рисунок 8 0 x

2. Найдем образы лучей (рис. 9)

Образы-лучи с удаленной точкой .

v Рисунок 9 0 u

Следовательно, образом полярной сетки полуплоскости является полярная сетка плоскости с разрезом вдоль положительной полуоси (рис. 9).

Задачи

1.1. Вычислить значения функций:

а) в точках где – целое число;

б) в точках ;

в) в точках ;

г) в точках ;

д) в точках ;

е) в точках .

1.2. Вычислить

1.3. Вычислить , подсчитав действительную и мнимую части с точностью до 0,0001.

1.4. Вычислить действительные и мнимые части функций: а) ; б) ;

в) .

1.5. Решить уравнение: .

1.6. Доказать тождества:

а) б)

1.7. Построить на комплексной плоскости образы точки при отображениях: а) б) в)

1.8. При отображении найти образ линии

1.9. При отображении найти образ прямоугольной сетки полуплоскости

1.10. При отображении, осуществляемом функцией Жуковского , найти образ линии