
- •Оглавление
- •Занятие 8. Полиномы. Действия над полиномами. Схема Горнера
- •Полиномы. Определение
- •Действия над полиномами
- •Алгоритм Евклида.
- •Занятие 10. Разложение полинома по степеням через схему Горнера. Кратные корни. Отыскание кратности корня с помощью схемы Горнера
- •10.1. Формула ТеЙлора, разложение полинома по степеням (через схему Горнера)
- •10.2. Кратность корней. Нахождение кратности корня с помощью схемы Горнера
- •10.2. Способ нахождения всех кратных корней
- •Занятие 9. Решение уравнений 3-й и 4-й степени
- •9.1. Решение уравнений 3-й степени
- •9.2. Решение уравнений 4-й степени
- •Занятие 12. Полиномы над полем . Приводимость. Полиномы над полем
- •12.1. Решение уравнений -й степени
-
Алгоритм Евклида.
Пусть
![]() .
Разделим
.
Разделим
![]() на
на
![]() с остатком:
с остатком:
![]() ;
;
![]()
![]() ;
;
![]()
![]() ;
;
![]()
![]() ,
где
,
где
![]()
![]()
![]() или последний, не
равный нулю остаток.
или последний, не
равный нулю остаток.
Упражнение 9.3. П 631 а).
9.3. Линейное представление НОД
Теорема 9.2. Пусть
![]() .
Тогда существуют полиномы
.
Тогда существуют полиномы
![]() такие, что
такие, что
![]()
Замечание 9.1.
Найти
![]() и
и
![]() можно с помощью алгоритма Евклида
аналогично тому, как искали линейное
представление НОД для целых чисел.
можно с помощью алгоритма Евклида
аналогично тому, как искали линейное
представление НОД для целых чисел.
Упражнение 9.4. П 632 а).
Теорема 9.3.
Полиномы
![]() взаимно просты (
взаимно просты (![]() )
тогда и только тогда, когда существуют
два полинома
)
тогда и только тогда, когда существуют
два полинома
![]() такие, что
такие, что
![]()
При этом будет выполняться
![]()
Упражнение 9.5. П 634 а).
Д/з: П 588, 641 d), c), 551, 541, 634 b), 636 a), 638.
Занятие 10. Разложение полинома по степеням через схему Горнера. Кратные корни. Отыскание кратности корня с помощью схемы Горнера
10.1. Формула ТеЙлора, разложение полинома по степеням (через схему Горнера)
Любую
![]() раз дифференцируемую в точке
раз дифференцируемую в точке
![]() функцию можно разложить в ряд Тейлора:
функцию можно разложить в ряд Тейлора:
![]()
где
![]() ,
если
,
если
![]() - полином.
- полином.
Определение
10.1. Назовем
такое представление разложением
![]() по степеням
по степеням
![]() .
.
Задача 1. Пусть имеется полином
![]()
Требуется разложить
![]() по степеням
по степеням
![]() ,
т. е. найти неизвестные коэффициенты в
разложении
,
т. е. найти неизвестные коэффициенты в
разложении
![]()
Эту задачу можно решать двумя способами:
1) Так как
![]() ,
то, раскрывая скобки по биному и подставив
в
,
то, раскрывая скобки по биному и подставив
в
![]() ,
получим разложение (трудоемко).
,
получим разложение (трудоемко).
2) можно воспользоваться схемой Горнера
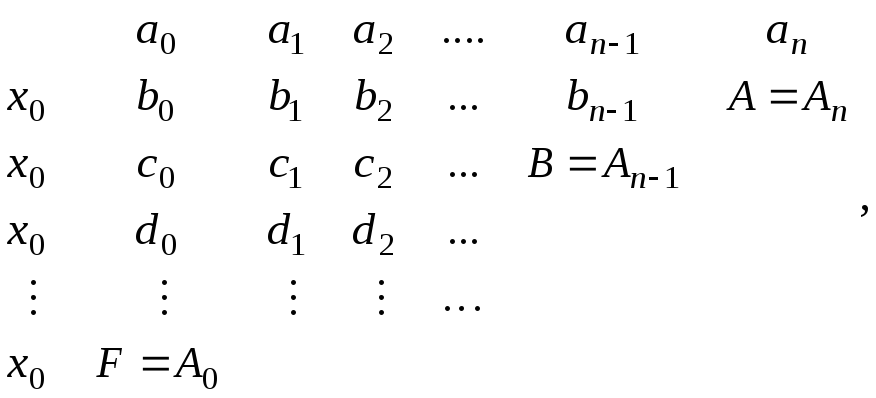
![]() В остальных строках
вычисляются
В остальных строках
вычисляются
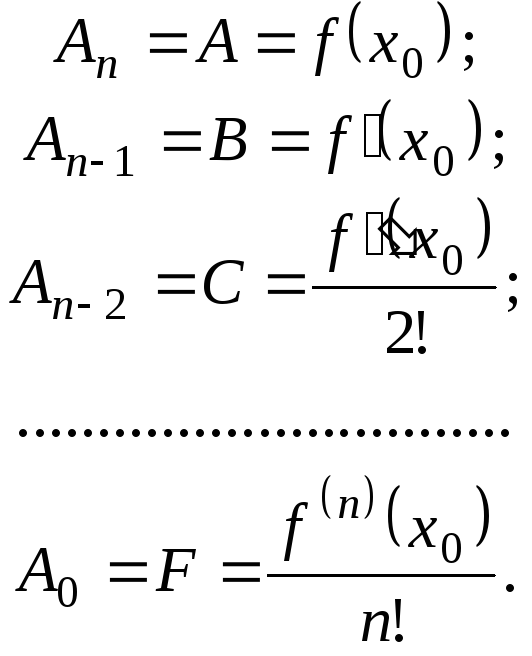
Пример 10.1.
![]()
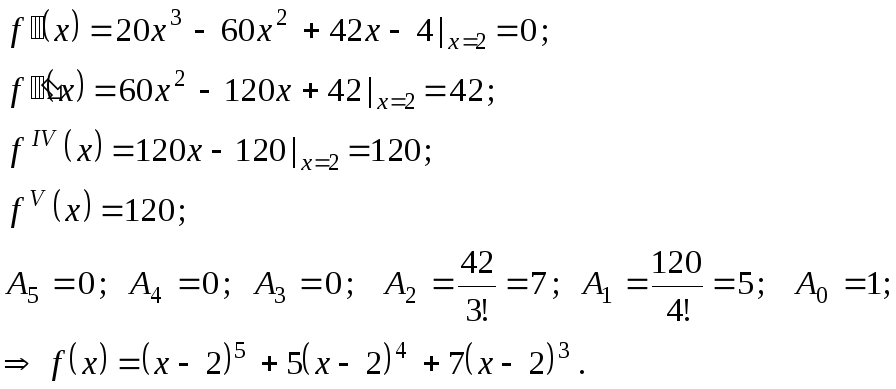
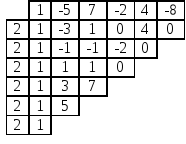
Замечание 10.2. Очевидно, что с помощью схемы Горнера возможно вычисление значений производных в точках.
10.2. Кратность корней. Нахождение кратности корня с помощью схемы Горнера
Пусть разложение
полинома
![]() на линейные множители
на линейные множители
![]()
Среди
![]() могут быть совпадающие. Если они есть,
то
могут быть совпадающие. Если они есть,
то
![]() (10.1)
(10.1)
где
![]() ,
а среди
,
а среди
![]() нет совпадающих.
нет совпадающих.
Определение
10.2. Если
![]() ,
то корень
,
то корень
![]() называется кратным
корнем кратности
называется кратным
корнем кратности
![]() ,
если
,
если
![]() то корень
то корень
![]() называется простым.
называется простым.
Задача 2. Имеет ли данный полином кратный корень? Если да, то какова его кратность?
Теорема
10.1. Пусть
![]() - кратный корень кратности
- кратный корень кратности
![]() полинома
полинома
![]() .
Тогда
.
Тогда
![]() является кратным корнем
является кратным корнем
![]() кратности
кратности
![]() .
.
![]()
![]()
![]()
![]()
где
![]() ,
,
![]() ,
,
![]()
![]()
Замечание 10.2.
![]() можно также найти по алгоритму Евклида.
можно также найти по алгоритму Евклида.
Итак, для того,
чтобы ответить на вопрос «имеет ли
данный полином кратный корень?»,
необходимо найти
![]() .
Если
.
Если
![]() ,
то «нет», иначе – «да».
,
то «нет», иначе – «да».
Если
корень λ
полинома
![]() известен,
то его кратность можно найти с помощью
схемы Горнера.
известен,
то его кратность можно найти с помощью
схемы Горнера.
Чтобы ответить на вопрос «какова кратность корня?», построим последовательность:
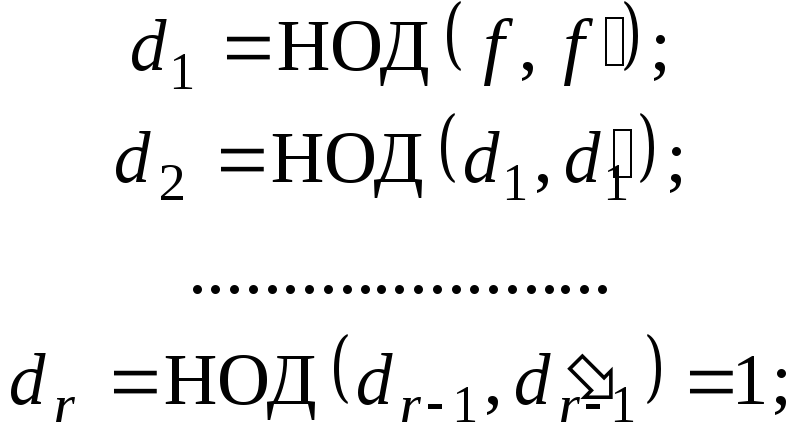
![]() имеет только
простые корни;
имеет только
простые корни;
![]() эти корни будут корнями кратности r
полинома
эти корни будут корнями кратности r
полинома
![]() .
.
Упражнение 10.1.
![]()
![]() можно найти корни.
Они будут кратными корнями
можно найти корни.
Они будут кратными корнями
![]() .
.
10.2. Способ нахождения всех кратных корней
Если уравнение
![]() достаточно большей степени и его решить
не удается, то построим
последовательность:
достаточно большей степени и его решить
не удается, то построим
последовательность:
![]()
т. к.
![]()
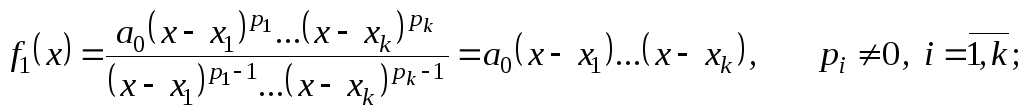
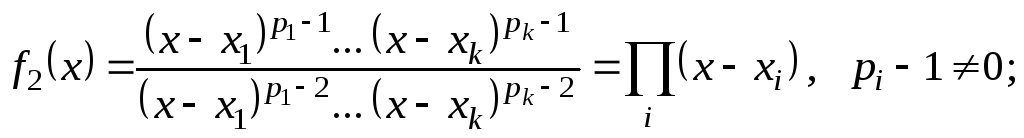
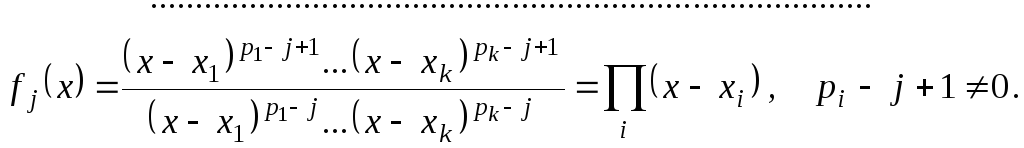
Так продолжаем до
тех пор, пока не найдется
![]() :
:

Все
корни полиномов
![]() –
простые, однако, среди корней полинома
–
простые, однако, среди корней полинома
![]() нет простых корней полинома
нет простых корней полинома
![]() (т. к. для простых корней полинома
(т. к. для простых корней полинома
![]() имеем
имеем
![]() ,
а в полином
,
а в полином
![]() входят корни, для которых
входят корни, для которых
![]() );
среди корней
);
среди корней
![]() нет корней кратности 2 полинома
нет корней кратности 2 полинома
![]() и
т. д.
и
т. д.
Следовательно, найдя полиномы
![]()
получим
полиномы
![]() ,
корни которых простые и являются корнями
кратности j
полинома
,
корни которых простые и являются корнями
кратности j
полинома
![]() ,
и представление:
,
и представление:
![]()
Замечание
10.3. Если
поделить
![]() на
на
![]() ,
то уйдут те простые корни
,
то уйдут те простые корни
![]() ,
которые содержатся в
,
которые содержатся в
![]() ,
следовательно, останутся только те,
которые в последующих членах ряда
,
следовательно, останутся только те,
которые в последующих членах ряда
![]() ,
,
![]() ,
не содержатся, следовательно, кратность
этих корней в полиноме
,
не содержатся, следовательно, кратность
этих корней в полиноме
![]() равна
1. Если поделить
равна
1. Если поделить
![]() на
на
![]() ,
то останутся
корни кратности j
в полиноме
,
то останутся
корни кратности j
в полиноме
![]() .
.
Замечание
10.4. Этот
способ определения кратности корней,
их существования, используется в случае,
когда сложно разложить
![]() на
линейные множители.
на
линейные множители.
Пример 10.2.
![]()
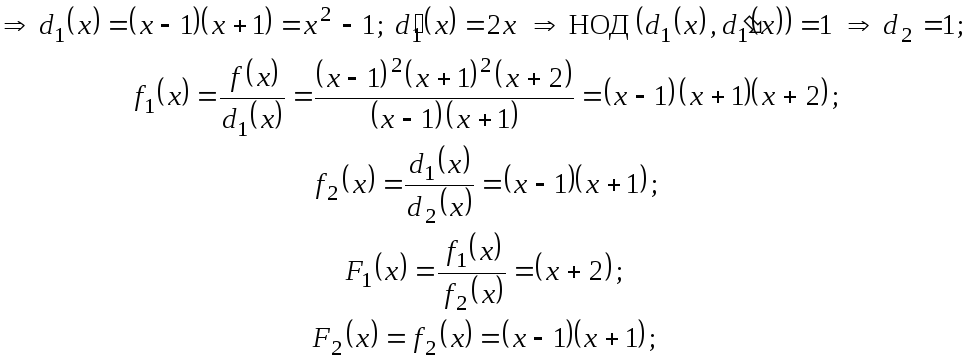
![]()
![]() - кратность 2,
- кратность 2,
![]() - кратность 1.
- кратность 1.
Замечание 10.5. Таким образом, схема Горнера используется:
-
для вычисления
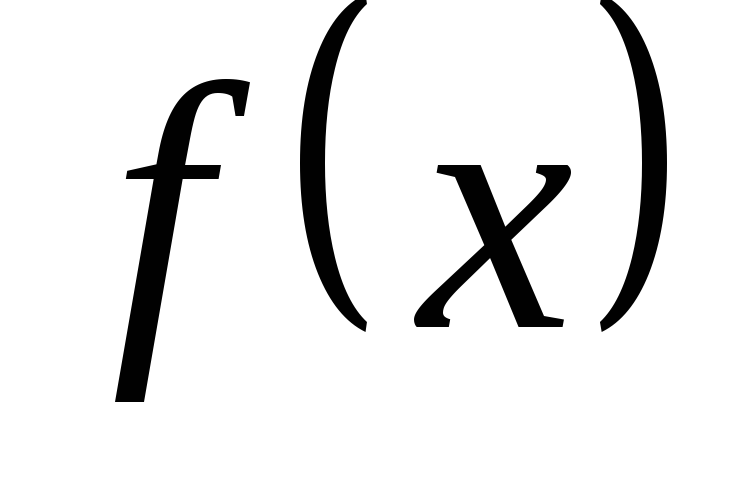 при
при
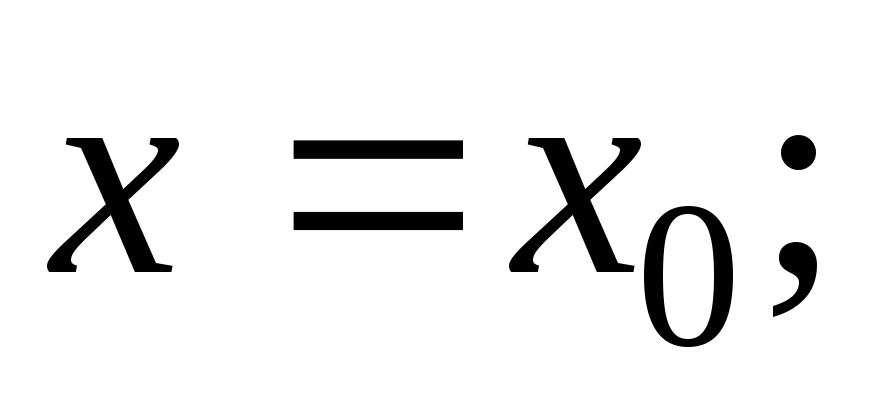
-
для вычисления полинома
 при делении
при делении
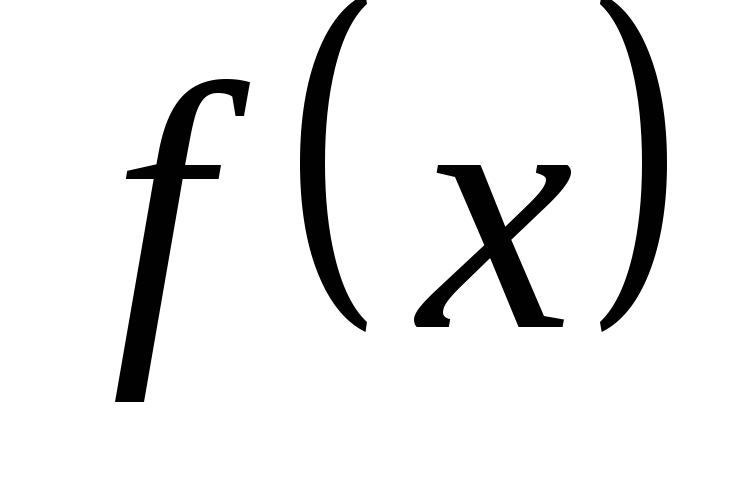 на линейный множитель
на линейный множитель
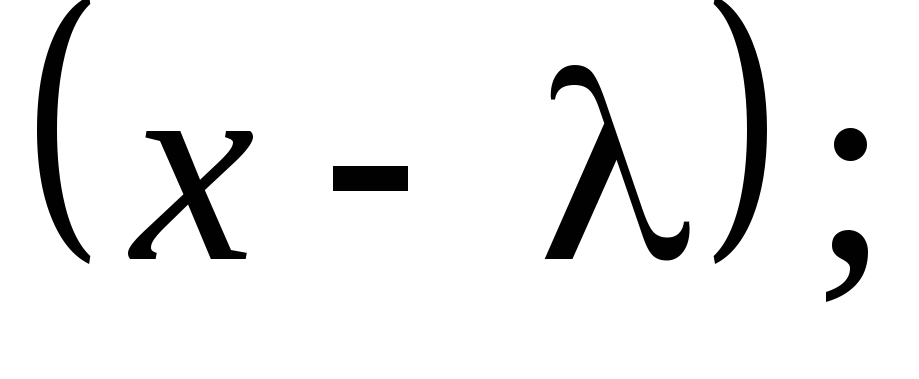
-
для вычисления производных
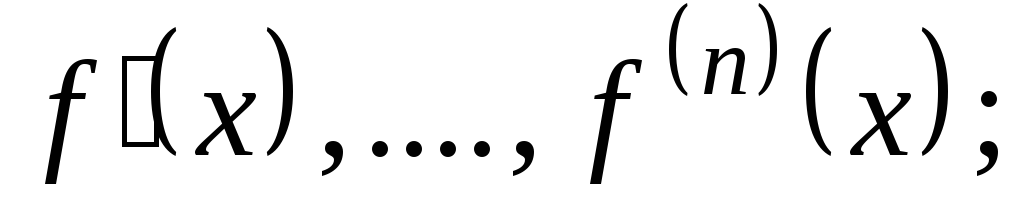
-
для разложения
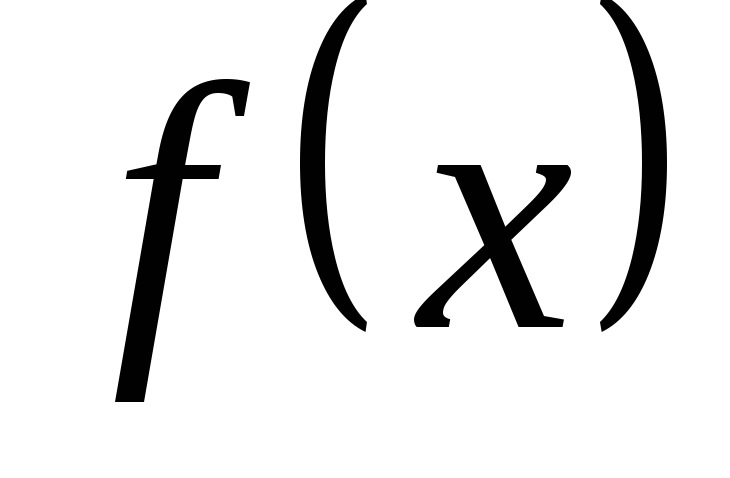 по степеням
по степеням
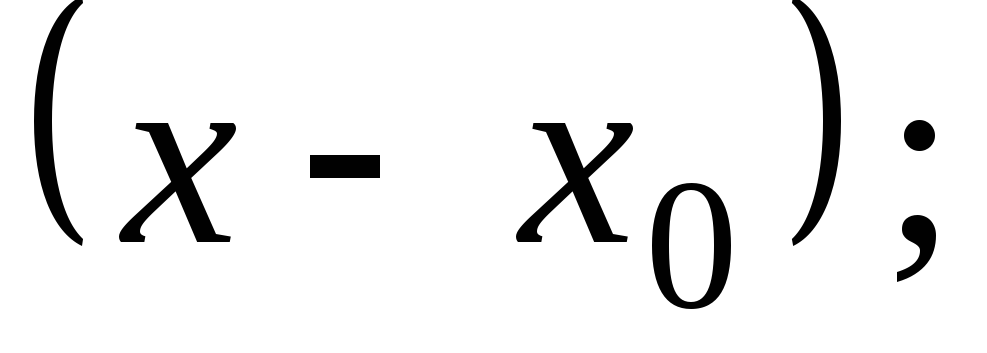
-
для определения кратности корня
 полинома
полинома
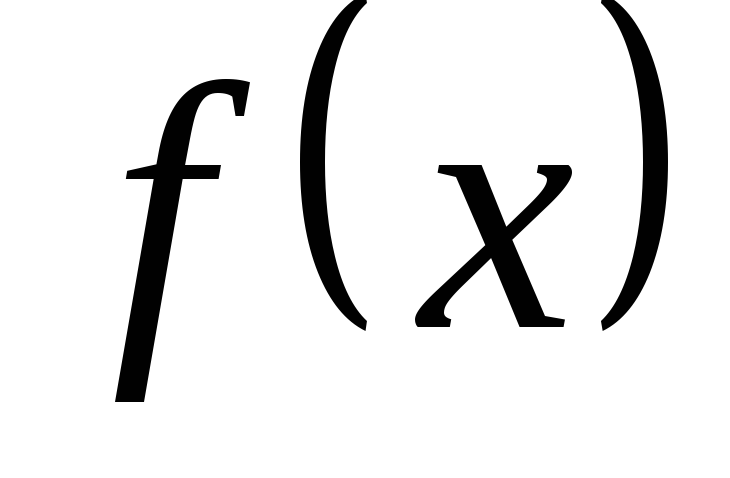 .
.
Д/з: П 541, 544 (b), 545 (d), 547, 548 (b), 549, 551, 588, 591, 631(b, c), 634 (b), 636 a), 638, 639 (a, b, c).
