5. Связность

Пусть граф G - неориентированный. Две вершины a и b называются связанными, если существует путь S с начальной вершиной a и конечной вершиной b, S=< a , a₁ , ... , a_n , b >. Если S проходит через какую-нибудь вершину a_i более одного раза, то можно, очевидно, удалить его циклический участок и при этом остающиеся ребра будут составлять путь S из a в b. Отсюда следует, что связанные путем вершины связаны и простым путем. Граф называется связным, если любая его пара вершин связана. Для всякого графа существует такое разбиение множества его вершин

на попарно непересекающиеся подмножества вершин V_i, что вершины в каждом V_i связаны, а вершины из различных V_i не связаны.

Граф H называется частью графа G, если множество его вершин V(H) содержится во множестве вершин V(G) графа G и все ребра H являются ребрами G. Для любой части H графа G существует единственная дополнительная часть (дополнение) , состоящее из всех ребер графа G, которые не вошли в H, и инцидентных им вершин. Особенно важным типом частей являются подграфы.

Пусть V^ -подмножество вершин графа G = < V, E >, V^  V. Подграф G(V^,E^), определяемый множеством V^, есть такая часть графа G, множеством вершин которой является V^, а ребрами - все ребра из G, оба конца которых лежат в V^:

= .

Тогда в соответствии с разбиением мы получаем прямое разложение

графа G на непересекающиеся связные подграфы G(V_i). Эти подграфы называются связными компонентами (или компонентами связности) графа G.

Теорема 3.2. Если в конечном неориентированном простом графе G ровно две вершины a₀ и b₀ имеют нечетную локальную степень, то они связаны.

Доказательство. По теореме 3.1, каждый конечный граф имеет четное число вершин нечетной степени. Так как это условие выполняется и для той компоненты G, которой принадлежит a₀ , то b₀ принадлежит той же компоненте связности. 

Теорема 3.3. Если неориентированный простой граф G имеет n вершин и k связных компонент, то максимальное число ребер в G равно

.

Доказательство. Пусть в графе G связная компонента G_i имеет n_i вершин. Тогда максимальное число ребер в G равно 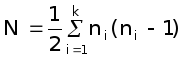. Это число достигается, когда каждый из графов G_i полный и имеет n_i вершин. Допустим, что среди графов G_i найдутся хотя бы два, которые имеют более одной вершины, например n₂  n₁ > 1. Построим вместо G другой граф G^ с тем же числом вершин и компонент, заменяя G₁ и G₂ полными графами G₁^ и G₂^ соответственно с n₁-1 и n₂+1 вершинами. Легко видеть, что это увеличит число ребер. Таким образом максимальное число ребер должен иметь граф, состоящий из k -1 изолированных вершин и одного полного графа с n - k + 1 вершинами.

Из теоремы 3.3 следует для случая k = 2 следующее утверждение.

Теорема 3.4. Простой неориентированный граф с n вершинами и с числом ребер, большим, чем

связен.

6. Деревья

Связный неориентированный граф называется деревом, если он не имеет циклов.

В частности, дерево не имеет петель и кратных ребер. Граф без циклов есть граф, связные компоненты которого являются деревьями; иногда такой граф называется лесом. Любая часть такого графа также будет графом без циклов.

Теорема 3.5. В дереве любые две вершины связаны единственным простым путем.

Доказательство. Любой путь в графе без циклов является простым. Если бы было два связывающих вершины простых пути, то был бы и цикл в дереве, что невозможно. 

Наглядное представление для произвольного дерева T = <V, E> можно получить при помощи следующей конструкции.

Выберем произвольную вершину a₀ и будем рассматривать ее как корень дерева или вершину нулевого уровня.

U₀ = {a₀}.

От a₀ проведем все ребра к вершинам, находящимся на расстоянии 1 от вершины a₀. Вершины, смежные с a₀ составят множество вершин первого уровня:

.

От этих вершин первого уровня проведем все ребра к смежным с ними вершинам, находящимся на расстоянии 2 от a₀ , за исключением ребер, инцидентных вершинам первого уровня. Получим множество вершин второго уровня

.

Из вершины a_i⁽ⁿ⁾ находящейся на расстоянии n от a₀ , выходит одно ребро к единственной предшествующей вершине , а также некоторое семейство ребер к вершинам , находящимся на расстоянии n +1.

.

Ни для какой из этих вершин a⁽ⁿ⁾ не может быть ребер, соединяющих ее с вершинами с тем же или меньшим расстоянием, кроме { a^(n-1), a⁽ⁿ⁾}. Таким образом, дерево может быть представлено в следующей форме:

Будем называть вершину a дерева концевой, если (a) = 1.

Будем называть ребро концевым, если хотя бы одна инцидентная ему вершина является концевой.

Утверждение 3.6. Любое нетривиальное конечное дерево имеет хотя бы две концевые вершины и хотя бы одно концевое ребро.

Доказательство совершенно просто может быть проведено, например, индукцией по числу вершин.

Утверждение 3.7. Каждое дерево с n вершинами имеет n-1 ребро.

Доказательство. Доказательство легко проводится индукцией по числу вершин. Для n =1 утверждение, очевидно, справедливо. Пусть n>1. Тогда в дереве существует концевая вершина v. Удаляя из дерева v и ребро (u, v), инцидентное v, получим дерево с n-1 вершиной, которое в силу индуктивного предположения имеет n-2 ребра. Следовательно, первоначальное дерево имеет n-2+1=n-1 ребро.

Обратимся теперь к вопросу о подсчете числа деревьев, которые могут быть построены на заданном множестве вершин. Подчеркнем, что речь идет не о подсчете числа различных попарно неизоморфных деревьев, а именно о числе деревьев, графы которых различны, то есть различаются хотя бы одним ребром (множество вершин фиксировано).

Пример. Пусть количество вершин n равно 4. Тогда на этом множестве вершин могут быть построены следующие различные деревья.

Первый класс таких деревьев составляют деревья следующего вида:

Концевые вершины для деревьев такого класса могут быть выбраны способами, при каждом таком выборе порядок внутренних вершин может быть выбран двумя способами. Получаем 12 различных деревьев, составляющих указанный класс.

Второй класс деревьев имеет вид:

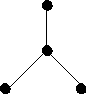
Центральная вершина может быть выбрана 4 способами, что дает 4 различных дерева в этом классе.

Других деревьев с 4 вершинами, отличных от указанных в первом и втором классах, нет. Таким образом, существует 16 деревьев, имеющих 4 фиксированные вершины. 

Обратимся теперь к общему результату.

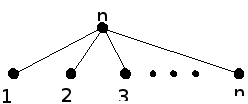
Теорема 3.8. Число различных деревьев, которые можно построить на заданном множестве V, содержащем n вершин, равно

t_n = n^n-2.

Доказательство. Обозначим элементы данного множества V, расположенные в некотором фиксированном порядке, числами

V = {1,2, ... ,n} (3.1)

Для любого дерева T, определенного на V, введем некоторый символ, характеризующий его однозначно. В T существуют концевые вершины. Обозначим через b₁ первую концевую вершину в последовательности (3.1), а через e₁ = {a₁ , b₁} - соответствующее концевое ребро. Удалив из T ребро E₁ и вершину b₁, мы получим новое дерево T₁ . Для T₁ найдется первая в списке (3.1) концевая вершина b₂ с ребром e₂ = {a₂ , b₂ }. Эта редукция повторяется до тех пор, пока после удаления ребра e_n-2 = (a_n-2 , b_n-2) не останется единственное ребро e_n-1 = (a_n-1 , b_n-1), соединяющее две оставшиеся вершины.

Тогда список

(T) = [a₁ , a₂ , ... , a_n-2 ] (3.2)

однозначно определяются деревом T и двум различным деревьям T и T^, очевидно, соответствуют разные символы такого вида. Каждая вершина a_i появляется в (3.2) (a_i) - 1 раз.

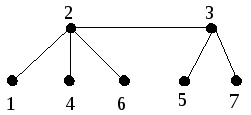
Для ясности приведем несколько примеров деревьев и соответствующих им последовательностей (T).

Примеры.

1.

2.

3.



Наоборот, каждая последовательность (3.2) определяет дерево T с помощью обратного построения. Если дана последовательность (3.2), то находится первая вершина b в списке (3.1), которая не содержится в (3.2). Это определяет ребро e₁ = {a₁ , b₁}. Далее удаляем вершины a₁ из последовательности (3.2) и b₁ из списка (3.1) и продолжаем построение для оставшихся элементов.

Получающийся в результате построения граф является деревом, что может быть установлено, например, по индукции. После удаления e₁ последовательность (3.2) будет содержать n - 3 элемента. Если она соответствует дереву T₁ , то граф T, получаемый из него добавлением e₁ , также есть дерево, так как вершина b₁ не принадлежит T₁ .

B (3.2) каждая вершина может принимать все n возможных значений. Все они соответствуют различным деревьям, откуда и получается формула t_n = n^n-2. 