1. Степени вершин

Граф называется конечным, если число его ребер конечно. При таком определении конечный граф может иметь бесконечное число вершин, но все они, кроме конечного числа, изолированные.

Пусть G - неориентированный граф. Число (x) ребер, инцидентных вершине x, называется локальной степенью, или просто степенью вершины x графа G. В каждом случае должно быть указано, считается петля однократной или двойной.

Пусть (a, b) = (b, a) - число ребер, соединяющих вершины a и b.

Очевидно, каждая степень каждой вершины есть сумма кратностей в вершине a:

.

Обозначим через n_{e =} n_e (G) число ребер в неориентированном графе G.

Так как каждое ребро учитывается в двух степенях в вершинах a и b, то. Формула остается справедливой и при наличии петель, если только в локальных степенях вершин считать их дважды. Поэтому

.

Отсюда следует

Теорема 3.1. 1 В конечном графе число вершин нечетной степени четно.

2. О машинном представлении графов.

Очевидно, что наиболее понятный и полезный для человека способ представления графа - изображение графа на плоскости в виде точек и соединяющих их линий - будет совершенно бесполезным, если мы хотим решать с помощью ЭВМ задачи, связанные с графами. Выбор соответствующей структуры данных для представления графов оказывает принципиальное влияние на эффективность алгоритмов.

В теории графов классическим способом представления графа служит матрица инциденций. Для графа G=<V, E> - это матрица I(G) с n строками, соответствующими вершинам, |V| = n, и с m столбцами, |E| = m, соответствующими ребрам. Для ориентированного графа столбец, соответствующий ребру < x, y > содержит 1 в строке, соответствующей вершине x, 1 в строке, соответствующей вершине y, и нули во всех остальных строках (петлю <x, x> иногда представляют значением 2). В случае неориентированного графа столбец, соответствующий ребру {x, y}, содержит 1 в строках, соответствующих x и y, и нули в остальных строках.

Пример.

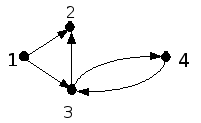
Рис. 3.2.

Для ориентированного графа, изображенного на рис. 3.2, матрица инциденций имеет вид:

<1,2> <1,3> <3,2> <3,4> <4,3>

С алгоритмической точки зрения матрица инциденций является, вероятно, самым худшим способом представления графа, который только можно представить. Во-первых, он требует mn ячеек памяти. Доступ неудобен. Ответ на элементарные вопросы типа “существует ли ребро <x,y>?”, “к каким вершинам ведут ребра из x?”, требует перебора всех столбцов матрицы.

Более удобным способом представление графа является матрица смежности (вершин), определяемая как матрица B = || b_{i j}|| размера nn, где b_{i j} = 1, если существует ребро, ведущее из вершины x в вершину y, b_{i j} = 0 в противном случае. Здесь мы подразумеваем, что ребро {x, y} неориентированного графа идет как от x к y, так и от y к x, так что матрица смежности такого графа всегда является симметричной. Ответ на вопрос типа “{x,y}E ?” может быть получен за один шаг.

Недостаток такого способа представления графа - nn ячеек занятой памяти независимо от числа ребер.

Более экономным в отношении требуемого объема памяти (особенно для неплотных графов m << nn) является метод представления графа с помощью списка пар. Пара (x, y) соответствует ребру <x, y>, если граф ориентированный, и ребру {x, y}, если граф неориентированный. Очевидно, что объем памяти в этом случае составляет 2m ячеек. Неудобство - большое число шагов, порядка m в худшем случае, необходимое для получения множества вершин, к которым ведут ребра из данной вершины.

Для приведенного на рис. 3.2. графа список пар имеет следующий вид:

(1, 2), (3, 2), (4, 3),

(1,3), (3, 4) .

Ситуацию можно значительно улучшить, упорядочив множество пар лексикографически и применяя двоичный поиск, но лучшим решением во многих случаях оказывается структура данных, которая называется списками инцидентности.

Она содержит для каждой вершины vV список вершин u, таких что < v, u >E (или { v, u }E в случае неориентированного графа). Для графа. представленного на рис. 3.2, список инцидентности имеет следующий вид:

Вершина	Список инцидентности
1	1		2		3	
2	2	
3	3		2		4	
4	4		3	

1



Каждый элемент списка инцидентности имеет вид

где