1.Исследование операций – комплекс научных методов для решения задач эффективного управления организационными системами.

2.Общая постановка задачи исследования операций

Введем обозначения:

a₁, a₂, ... – постоянные факторы,

х₁, х₂, ... – зависимые факторы.

Z = f(a₁,a₂,...,х₁,х₂,...) – целевая функция,

j _i(X) { ³ , = , ≤ } b _i – ограничения задачи в виде неравенств и (или) уравнений, (1 ≤ i ≤ m), где Х = ( х_1, х₂, ...., х _n ) ^Т – вектор искомых решений.

Предположим, что математическая модель операции построена; она позволяет вычислить показатель эффективности Z при любом принятом решении, для любой совокупности условий, в которых выполняется операция.

Все факторы, от которых зависит Z, делятся на две группы:

1) заранее известные (заданные) факторы α₁, α₂,…., на которые мы влиять не можем;

2) зависящие от нас факторы (элементы решения) х₁, х₂,…., которые мы в известных пределах, можем выбирать по своему усмотрению.

На множество решений наложены определенные ограничения, которые не могут быть нарушены. Например, материальные ресурсы, технические характеристики используемых машин и механизмов и т.д. Эти ограничения формируют множество возможных (допустимых) решений.

Показать эффективность Z зависит как от заданных условий, так и от элементов решения: Z = Z (α₁, α₂,..., х₁, х₂,...)

Задачу можно сформулировать следующим образом:

при заданных условиях α₁, α₂,…. найти такие элементы решения х₁, х₂,…, которые обращают показатель эффективности Z в максимум (минимум).

3.Классификация задач исследования операций

1. По наличию информации о переменных:

А) Детерменированные (задачи в условиях полной определенности).

Б) Стохастические (задачи принятия решений в условиях риска, если известны априорные вероятностные характеристики изучаемого объекта).

С) Задачи в условиях неопределенности (в задаче отсутствует информация об априорных вероятностях).

2. По учету фактора времени:

А) Динамические (многоэтапные задачи с учетом параметра времени).

Б) Статические (моделирование и принятие решений осуществляется в предположении о независимости от времени).

3. По числу критериев:

А) Сложные (многокритериальные).

Б) Простые (однокритериальные).

4. По характеру изменения переменных:

А) Дискретные.

Б) Непрерывные.

5. По характеру взаимосвязи между переменными:

А) Линейные.

Б) Нелинейные.

4.Разделы математического программирования: линейное (ЛП); нелинейное (НП); динамическое (ДП); целочисленное (ЦП); дробно-линейное; дискретное; параметрическое.

5.Линейное программирование (ЛП) – это раздел математического программирования, изучающий экстремальные свойства линейных целевых функций, на переменные которых наложены линейные ограничения.

6.Этапы операционного исследования:

1. постановка задачи;

2. построение содержательной модели рассматриваемого процесса;

3. формулировка цели и описание системы ограничений;

4. разработка математической модели с использованием математического аппарата;

5. решение задачи, поставленной на базе математической модели существующими методами или специально разработанными;

6. проверка полученных результатов расчета на их адекватность природе изучаемой системы (проверка достоверности результатов – технический термин, «робастость» модели – экономический и социологический термин) и возможная корректировка первоначальной модели;

7. реализация решения на практике.

7.Общим для задач, решаемых в рамах исследования операций, является поиск наибольшего или наименьшего, т.е. оптимального решения некоторой функции, отражающей цель исследования. Такая функция называется целевой.

Поиск оптимального решения (плана для экономических задач) осуществляется на некотором подмножестве, называемом множеством допустимых решений (МДР) или областью допустимых решений (ОДР).

8.Формы записи задач линейного программирования

1. Развернутая форма записи

Z = с₁х₁ + с₂х₂ + ...+ с_nх_n ® max ( min ),

а₁₁х₁ + а₁₂х₂ +...+ а_1nх_n = в_1,

а₂₁х₁ + а₂₂х₂ +...+ а_2nх_n = aв_2,

_……

а_m1х₁ + а_m2х₂ + ...+ а_mnх_n = в_m,

х₁ ³ 0, х₂ ³ 0, …, х _n ³ 0

2. Сокращенная форма записи

х _j ³ 0, (1 ≤ j ≤ n)

3. Матричная форма записи

Z = CX ® max ( min ),

где C = (с₁, с₂, ..., с_n), Х = (х₁, х₂, ...., х_n)^Т

АХ = В, Х ³ 0

где В = (в₁, ... в_i , ... , в_m)^Т , А =

4. Векторная форма записи

Z = C*X ® max (min),

где C = (с₁, с₂, ..., с _n), Х = (х_1, х₂, ...., х _n).

Где C*X – скалярное произведение векторов С и Х.

Ограничения задачи в векторной форме:

А₁х₁ + А₂х₂ + ... + А_nх_n= В

Данная запись означает разложение вектора по векторам А₁, ..., А_n,

где В = (в₁, ..., в_i , ..., в_m)^Т , А _j = (а_{1 j}, а_{2 j}, ..., а_{m j})^Т

9.Классификация задач линейного программирования по системе ограничений:

1. Основная (каноническая) задача линейного программирования

В качестве ограничений задача содержит систему линейных алгебраических уравнений:

Z = CX ® max ( min ), (I)

АХ = В, (II)

Х ³ 0, (III)

Где С = (с₁,..,с _j ,.., с_n), В = (b₁,...b_i ,...b_m) ^Т, Х = (х₁, х₂, ...., х_n)^Т

А =

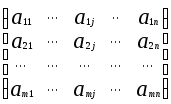
2. Стандартная задача линейного программирования

Задача ограничена неравенствами:

Z = CX ® max ( min ), (I)

АХ ≥ В, (II)

Х ³ 0, (III)

Где С = (с₁,..,с _j ,.., с_n), В = (b₁,...b_i ,...b_m) ^Т, Х = (х₁, х₂, ...., х_n)^Т

А =

3. Общая (смешанная) задача линейного программирования

Задача имеет ограничения в виде уравнений и неравенств:

Z = с₁х₁ + с₂х₂ + ...+ с_nх_n ® max ( min ),

а₁₁х₁ + а₁₂х₂ + ... + а_1nх_n = b_1,

а₂₁х₁ + а₂₂х₂ + ...+ а_2nх_n = b_2,

...

а_к1х₁ + а_к2х₂ +...+ а_кnх_n = b_к,

а_{к+1, 1} х₁ + а_{к+1, 2} х₂ +...+ а_{к+1, n} х_n ≤ b_к,

...

а_m1х₁ + а_m2х₂ + ...+ а_mnх_n ≤ b_m,

х₁ ³ 0, х₂ ³ 0, …, х _n ³ 0

10. Определение базисного решения, вилы базисных решений, их количество.

Пусть целевая функция ЗЛП в качестве ограничений содержит систему m уравнений с n переменными:

Z = с₁х₁ + с₂х₂ + ...+ с_nх_n ® max ( min ), ( I )

а₁₁х₁ + а₁₂х₂ + ... + а_1nх_n= b_1, (II)

а₂₁х₁ + а₂₂х₂ + ... + а_2nх_n= b_2,

_……

а_m1х₁ + а_m2х₂ + ... + а_mnх_n = b_m,

Условия неотрицательности переменных:

х₁ ³ 0, х₂ ³ 0, …, х _n ³ 0 (III)

Необходимо найти n неотрицательных значений переменных

х₁, х₂, …, х _n, удовлетворяющих условиям ( II ), (III) и обращающих в максимум (минимум) целевую функцию ( I ).

В каких случаях задача не имеет решений?

Основная ЗЛП неразрешима, если:

1. уравнения ( II ) не совместны;

2. уравнения (II) совместны, но решения не удовлетворяют условиям неотрицательности;

3. уравнения (II) совместны, существуют допустимые решения, но среди них нет оптимальных.

Предположим, что система равнений совместна, т.е. ранг основной матрицы = рангу расширенной, но при этом количество переменных больше, чем ранг. В этом слчае система будет иметь множество решений и переменные задачи подразделяют на основные (базисные) и не основные (свободные). Множество решений ищется на основе варьирования значений свободных переменных. Базисное решение – решение, в котором свободные переменные принимают нулевые значения.

Базисные решения:

• допустимые – все компоненты не отрицательные

• не допустимые – если хотя бы одно значение компонента отрицательное

• вырожденные – кроме основных переменных нулевые значения принимает хотя бы одна из основных переменных

Количество базисных решений: C ^m_n = , где m – количество уравнений (ранг матрицы), n – количество переменных.