1.3. Модулированные колебания

Амплитудная и фазовая модуляции. Любой колебательный процесс, отличный от гармонического, называется модулированным колебанием. Примеры таких процессов (их осциллограммы) приведены на рис. 1.7.

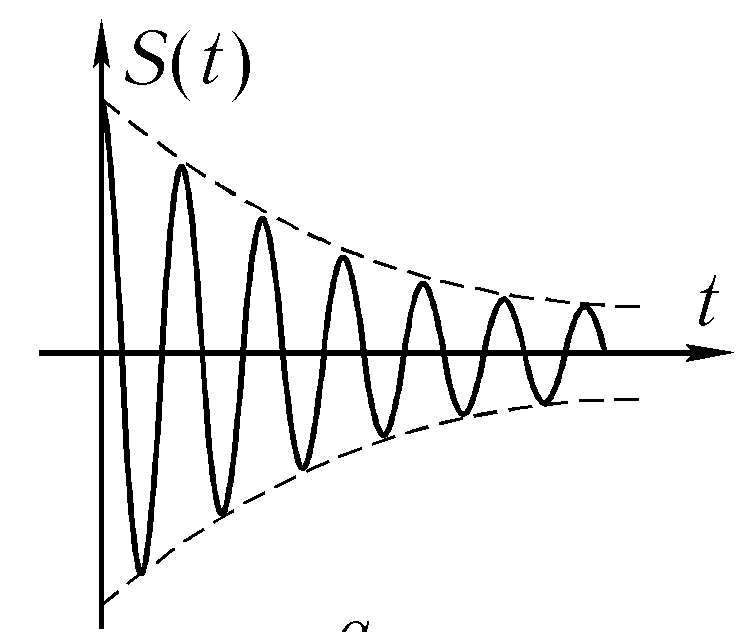
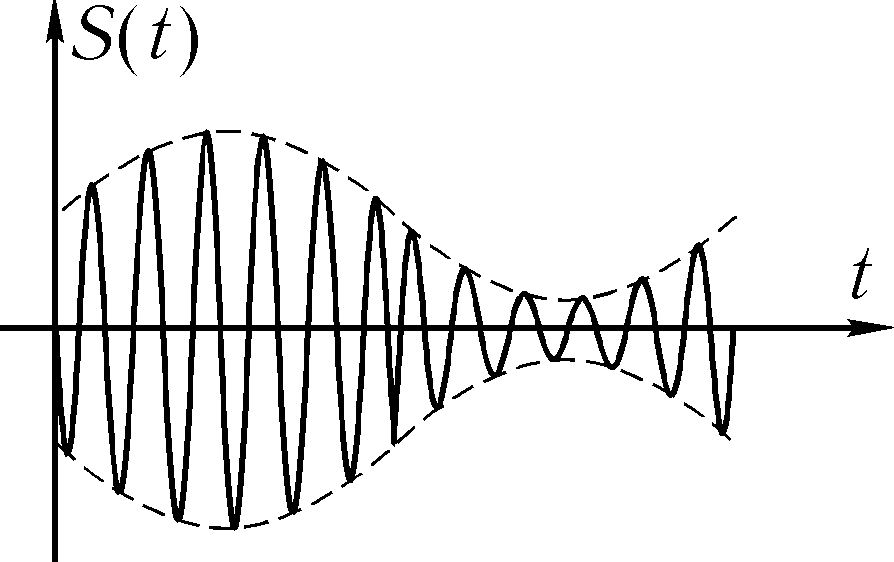
Рис. 1.7

Будем записывать модулированное колебание в виде

S(t) = a(t) cos(ω₀t + φ(t)). (1.15)

В отличие от гармонического колебания, здесь a(t) и φ(t) — меняющиеся во времени величины. Форма записи (1.15) особенно целесообразна в том случае, когда a(t) и φ(t) — медленно меняющиеся функции времени. Что означает медленность изменения функций a(t) и φ(t)? Рассмотрим наряду с модулированным колебанием (1.15) гармоническое колебание

S₀(t) = а₀ cos(ω₀t + φ₀). (1.16)

Здесь ω₀ — частота гармонического колебания, та же самая константа, которая входит в выражение (1.15).

Рассмотрим интервал времени τ, существенно превышающий период гармонического колебания S₀(t):

τ >> 2π/ω₀ (1.17)

и пусть на этом интервале функции a(t) и φ(t) остаются практически неизменными. Причем:

a(t) = а₀ и φ(t) = φ₀. (1.18)

Итак, мы рассматриваем модулированное колебание, в котором на интервалах времени т, больших по сравнению с периодом T₀ соответствующего гармонического колебания, величины a(t) и φ(t) остаются практически неизменными. В большинстве физически интересных ситуаций достаточно полагать, что сильное неравенство (1.17) выполнено, если интервал времени τ на один-два порядка превышает период колебаний 2π/ω₀. Такое

модулированное колебание называется квазигармоническим. В этом случае медленно

меняющиеся величины a(t) и (p(t) называют амплитудой и, соответственно, начальной фазой модулированного колебания. Итак, квазигармоническое колебание можно характеризовать двумя параметрами: периодом колебаний T₀ = 2π/ω₀ и временем τ >> T₀, характеризующим быстроту изменения амплитуды a(t) и (или) начальной фазы φ(t). Для описания модулированных колебаний используется следующая терминология: говорят, что функция a(t) описывает закон амплитудной модуляции, а функция φ(t) — закон фазовой модуляции.

Если φ(t) = φ₀ = const, то

S(t) = a(t) cos(ω₀t + φ₀), (1.19)

где a(t) > 0.

Такое колебание называют модулированным по амплитуде.

Если a(t) = а₀ = const, то

S(t) = а₀ cos[ω₀t + φ(t)]. (1.20)

Это — колебание, модулированное по фазе. В общем случае имеем как амплитудную, так и фазовую модуляцию, т. е. колебание вида (1.15).

Так же, как и гармонические колебания, квазигармонические процессы изображают графически в виде векторов. Если гармоническое колебание S₀(t), описываемое формулой (1.17), изображается вектором S₀, имеющим фиксированную длину а₀ и направление φ₀ (т. е. мы как бы смотрим на вращающийся с угловой скоростью ω₀ вектор S₀ из системы координат, которая вращается с той же угловой скоростью — и поэтому видим неподвижный вектор), то дулированное колебание на той же векторной диаграмме естественно изобразить в виде вектора, длина которого a(t) и (или) угол наклона φ(t) медленно изменяются (медленно, если речь идет о квазигармоническом колебании).

В частности, амплитудно-модулированное колебание (1.19) изображается вектором неизменного направления φ₀, длина которого изменяется (рис. 1.8 а), а колебание (1.20), модулированное по фазе — вектором неизменной длины, угол наклона которого φ(t) изменяется: (качания вектора на рис. 1.8 б).

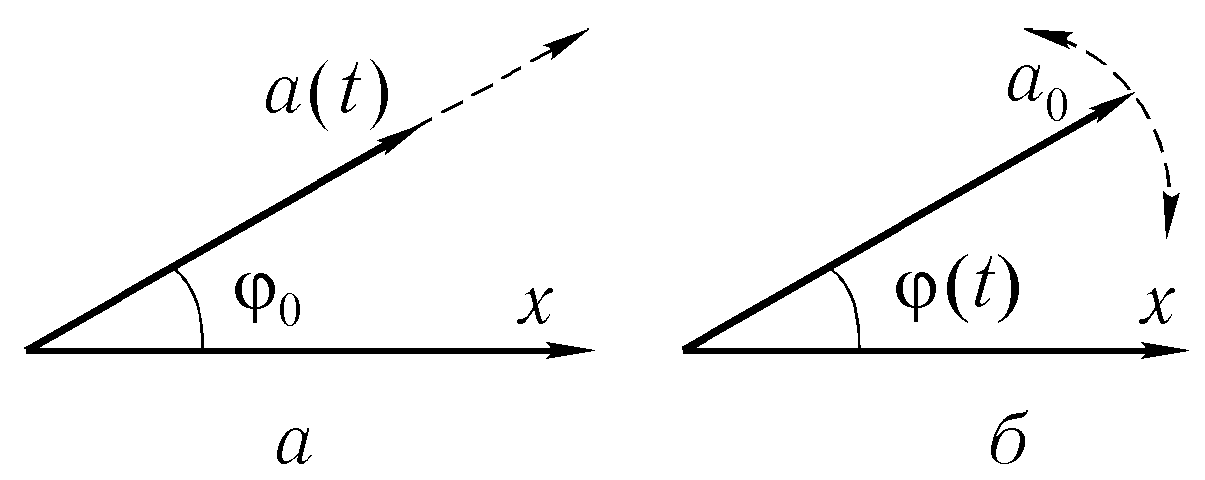
Аргумент косинуса в (1.20) называют фазой модулированного колебания

Ф(t) = ω₀t + φ(t)

причем в отличие от гармонического колебания, скорость изменения фазы Ф

(величина, которую можно назвать частотой ω), является функцией времени

ω(t) = Ф' (t) = ω₀ + φ' (t) ` (1.21)

Если выполнено условие квазигармоничности (1.17), то φ' (t) << ω₀, т. е.

меняющаяся во времени частота ω(t) мало отклоняется от частоты ω₀ гармонического колебания (1.16).

Отметим также, что если φ(t) меняется по линейному закону φ(t) = Ω, то мы получаем из (1.21)

ω = ω₀ + Ω, (1.22)

т. е. просто гармоническое колебание со смещенной частотой, причем Ω<<ω₀

при условии (1.18).

В системе координат, в которой гармоническое колебание частоты ω₀ изображается неподвижным вектором, колебание с частотой ω = ω₀ + Ω, изображается вектором, медленно вращающимся против часовой стрелки с частотой Ω, если Ω > 0 (и по часовой стрелке при Ω < 0).

Осциллограммы процессов на рис. 1.7 (а; б) являются примером амплитудно-модулированных колебаний, а на рис. 1.7 в — пример колебания, модулированного по фазе.

Биения. Рассмотрим модулированное колебание

S(t) =a(t) cos ω₀t, (1.23)

где закон модуляции a(t) имеет вид

a(t) =a₀cos Ωt. (1.24)

Будем полагать изменения a(t) медленными, т. е. множитель cosω₀t множество раз изменяет знак (проходит много периодов несущего колебания) прежде, чем значение a(t) заметно изменится. Другими словами, период изменения функции a(t) (равный Т = 2π/Ω) много больше периода несущего колебания 2π/ω₀= T₀:

ω₀ >> Ω. (1.25)

Колебание (1.23) с законом модуляции (1.24) изображено на рис. 1.9. Такое квазигармоническое колебание (конечно, не очень строго) называют гармоническим колебанием с медленно меняющейся амплитудой.

Рассмотрим физический пример. Пусть рупор громкоговорителя является источником

гармонического звукового колебания. Например, он излучает звуковую волну с частотой

ν₀ = 440 герц (ω₀ = 2πν₀). Это — нота «ля» первой октавы. Мы слышим ровный музыкальный тон — гармоническое колебание S₀(t) = a₀ cos ω₀t. Как получить модулированное колебание (1.23)? Будем периодически то открывать, то закрывать перегородкой излучающий рупор, громкость звука будет периодически изменяться (например, с частотой 1 раз в секунду (Ω = 2π рад/с)). Звуковые колебания мы будем воспринимать как чистый звуковой тон с частотой ω₀, громкость которого периодически изменяется.

А теперь обратим внимание на элементарное тригонометрическое тождество

cos ω₁t + cosω₂t = 2 cos ((ω_l - ω₂ )t/2) cos ((ω_l+ω₂ )t/2),

которое показывает, что, то же модулированное колебание (1.23) с законом модуляции (1.24) можно получить, сложив два гармонических колебания, немного отличающиеся по частоте:

Затухающие колебания

При действии тормозящих сил(трения) механическая энергия тратится на преодоление этих сил и колебания затухают

Если силу трения выразить в виде

F=-

И подставить в правую часть уравнения колебаний

;

То после преобразований получается каноническое уравнение затухающих колебаний

Подстановка

, , приводит к характеристическому уравнению

;

,

=,

где - комплексные постоянные

ω=

требование вещественности решения

;

Учитывая это, представим коэффициенты в виде

Возьмем ; , где - постоянные(неизвестные).

Тогда

q=aexp(-βt)cos(ωt+α)

T=2/ω=2/

A(t)/A(t+T)= exp(βТ) - декремент затухания

γ=ln(A(t)/A(t+T))= βТ - логарифмический декремент затухания – величина обратная числу колебаний за время релаксации

τ = 1/γ – время релаксации

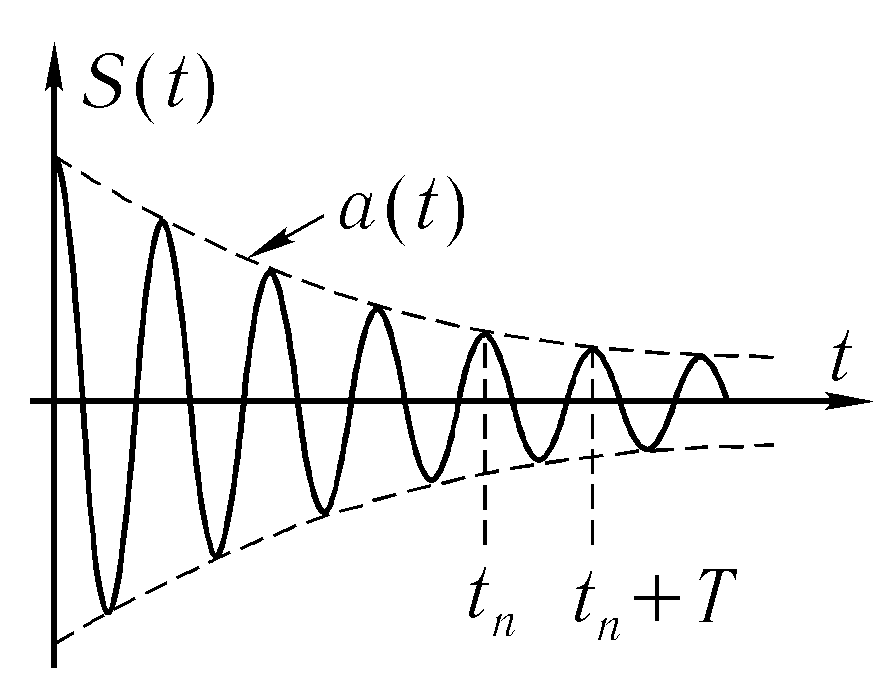
Если β² >ω² то корни характеристического уравнения вещественны

Решение уравнения имеет вид экспонент

Множители при времени положительны и коэффициенты С₁ и С₂

также положительны

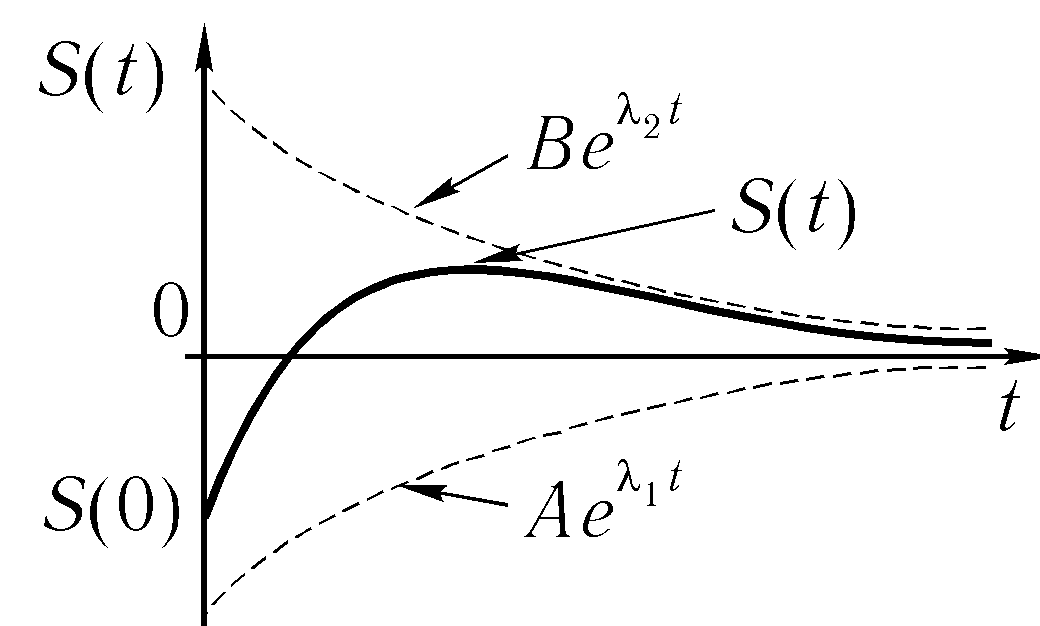
Т.е. при сильном трении колебания не возникают – выведенная из положения равновесия система возвращается в это положение асимптотически. Система может пройти через положение равновесия, отклонится в другую сторону и только потом приблизится к положению равновесия асимптотически.

Колебания являются апериодическими(непреодическими)

Процесс возвращения системы в положение равновесия зависит от соотношения коэффициентов С₁ и С₂

Лекция№11

Вынужденные колебания – колебания под действием вынуждающей силы

Например, если сила изменяется по косинусоидальному закону, то уравнение колебаний имеет вид

где в правой части уравнения - сила трения, вынуждающая сила.

- ускорение, остальное – сумма сил, отнесенная к массе тела.

Это линейное неоднородное дифференциальное уравнение с постоянными коэффициентами

Для решения дифференциального уравнения применяется следующий прием- в правой части формируется комплексное число путем добавления мнимой части, затем решается уравнение и мнимая составляющая в решении отбрасывается согласно условию равенства комплексных чисел

После добавления мнимой составляющей в правой части уравнение приобретает вид

=

Комплексное число переводится в экспоненциальную форму

Решение ищется в виде комплексной экспоненты

;

Тогда первая производная

;

Вторая производная

Подстановка в дифференциальное уравнение дает

Сокращая на экспоненту, получаем выражение для коэффициента

,

где

Или в форме

;

Тогда решение дифференциального уравнения можно записать

Амплитуда меняется с частотой. При этом имеет место экстремум амплитуды.

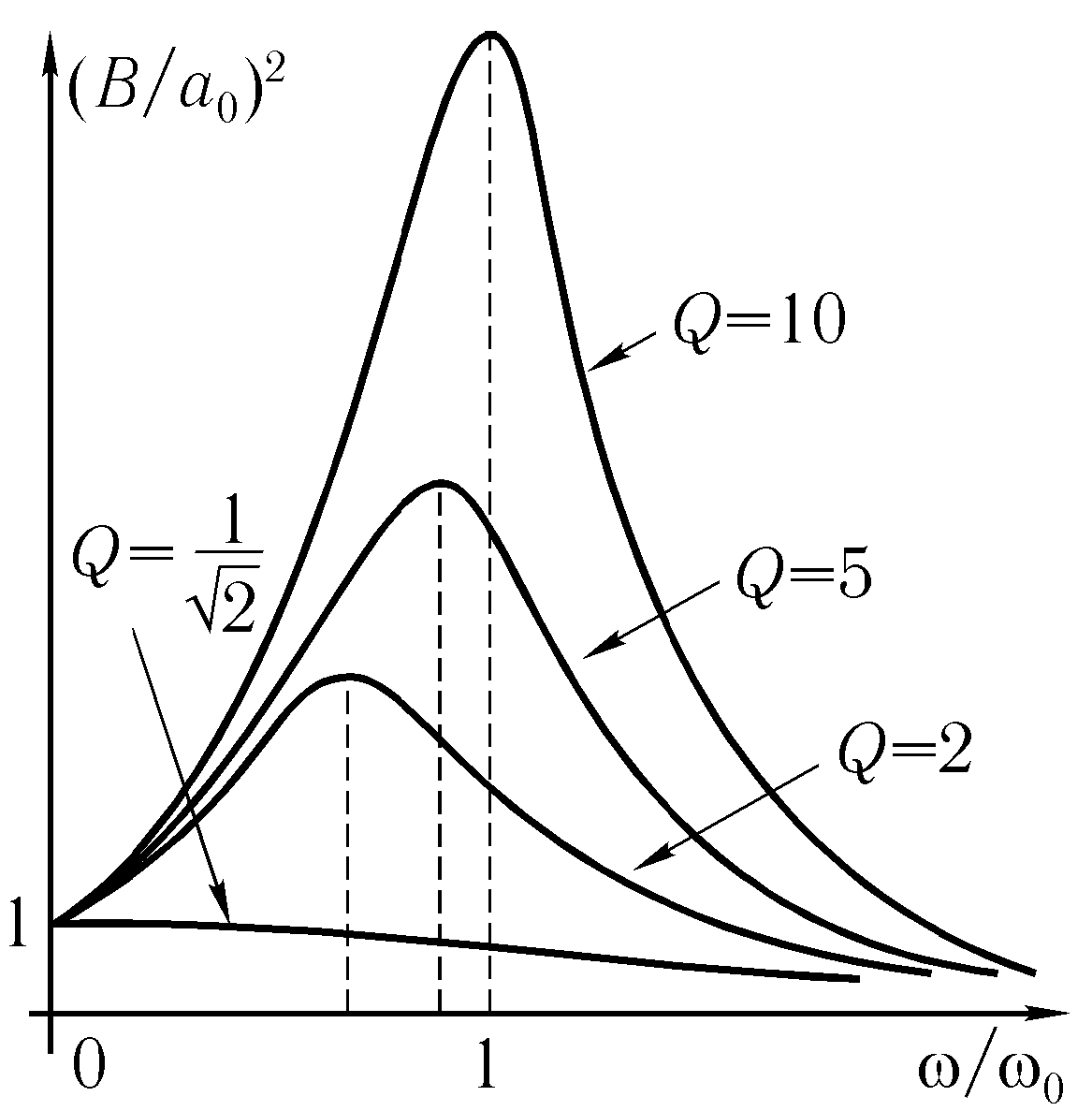
Зависимость амплитуды колебаний от частоты

Точка экстремума резонансная частота, амплитуда имеет максимум

Из условия равенства нулю производной от амплитуды

по частоте

определяем резонансную частоту

- резонансная частота