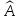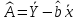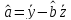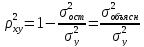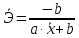МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ

ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«УДМУРТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»

ИНСТИТУТ ЭКОНОМИКИ И УПРАВЛЕНИЯ

КАФЕДРА МАТЕМАТИЧЕСКИХ МЕТОДОВ В ЭКОНОМИКЕ

Лабораторная работа

на тему: «Нелинейная парная регрессия»

по дисциплине «Эконометрика»

Вариант 9

Выполнил студент гр. 061800-31	Нуриева Г. Р.
Проверил Ассистент кафедры «Математических методов экономике»	Неустроев Г.В.

Ижевск, 2011 г.

Содержание

Постановка задачи 3

Решение задачи 4

Вывод 9

Приложение 1 10

Приложение 2 12

Приложение 3 22

Приложение 4 29

Приложение 5 37

Приложение 6 55

Приложение 7 69

Постановка задачи

Определить регрессию пенсий на заработную плату за 2006 г. по данным, приведенным в приложении 1.

1. Постройте поле корреляции и сформулируйте гипотезу о форме связи (необходимо построить график распределения зависимой переменной от независимой).

2. Рассчитайте параметры уравнений степенной, экспоненциальной, полулогарифмической, обратной и гиперболической парной регрессии.

3. Оцените тесноту связи с помощью показателей корреляции и детерминации.

4. Дайте с помощью среднего коэффициента эластичности сравнительную оценку силы связи фактора с результатом.

5. Оцените качество уравнений с помощью средней ошибки аппроксимации.

6. Оцените статистическую надежность результатов регрессионного моделирования с помощью F-критерия Фишера.

7. По значениям характеристик, полученных в предыдущих заданиях, выберите лучшее уравнение регрессии и дайте его обоснование.

Решение задачи

1. Построим поле корреляции:

Рис. 1. Поле корреляции (график рассеивания исходных данных)

По графику можно сделать вывод, что представленную зависимость можно описать с помощью модели линейной парной регрессии, а также рассмотрим следующие модели парной регрессии: степенную, экспоненциальную, полулогарифмическую и гиперболическую парные регрессии.

2. Рассчитаем параметры данных уравнений парной регрессии

а) Для начала рассмотрим степенную парную регрессию: Она приводится к линейному виду путем логарифмирования:

Для удобства вычислений составим таблицу (Приложение 2). Итоговые вычисления представлены в таблице 1.

Так, получаем следующее уравнение: которое после преобразований примет следующий вид:

б) следующая модель — гиперболическая: Сделаем замену , и приведем модель к линейному виду:

Вычисления представлены в приложении 3, а итоговые результаты в таблице 1.

Получаем следующее уравнение:

в) Для полулогарифмической модели характерно уравнение:  делаем замену: .

Итоговые оценки параметров представлены в таблице 1, промежуточные вычисления в приложении 4. В результате вычислений получаем уравнение: .

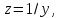г) обратная модель имеет следующий вид: Сделаем замену и приведем модель к линейному виду: Вычисления представлены в приложении 5, а итоговые результаты в таблице 1.

д) экспоненциальная модель: Приведем данную модель к линейному виду: Вычисления представлены в приложении 6, а итоговые результаты в таблице 1.

Так, получается следующее уравнение: которое после преобразований примет вид: .

Таблица 1

Параметры уравнений парной регрессии

Функции	Степенная	Гиперболическая	Полулогарифмическая	Обратная	Экспоненциальная
				—
	5,71	2883,856	2883,856	—	5,71
		—	—
	6,32	—	—	9516,823	9516,823
	—				—
	—	0,00012	6,32	0,0003549	—
	0,3867	-11204048,102	1267,805	-0,00000001052	0,000034
		—	—	—
	4,4369	—	—	—	7,629
					—
	1,49	4207,505	-8647,791	0,000455	—

3. Оценим тесноту связи с помощью индексов корреляции и детерминации. Расчеты приведены в таблице 2.

Таблица 2

Оценка тесноты связи

Параметры	Степенная модель	Гиперболическая модель	Полулогарифмическая модель	Обратная модель	Экспоненциальная модель
	260687,6	260687,6	260687,6	260687,6	260687,6
	66360,26	106134,12	73775,82	66820,22	58396,11
	0,8634	0,77	0,8468	0,8624	0,8809
	0,7454	0,5929	0,717	0,7437	0,776

Индекс корреляции показывает значительность связи. После проведения оценки тесноты связи, можно сказать, что он выше у экспоненциальной модели и равен 88,09%. Самый низкий из приведенных моделей — у гиперболической модели (77%). Индекс детерминации характеризует долю дисперсии, объясненную моделью. У экспоненциальной модели этот показатель также выше по сравнению с другими и равен 0,776. Он показывает, что уравнение регрессии объясняется на 77,6% дисперсией результативного признака, на долю же прочих факторов приходится 22,4%. Оба этих индекса не превышают значений коэффициентов корреляции и детерминации линейной модели парной регрессии. Эти показатели равны 88,27% и 77,91% соответственно.

4. Найдем средний коэффициент эластичности

Для расчетов среднего коэффициента эластичности приведена таблица 3. Он вычисляется по формуле:

Таблица 3

Средние коэффициенты эластичности

Модель	Степенная	Гиперболическая	Полулогарифмическая	Обратная	Экспоненциальная
Формула
Значение	0,386695	0,388516	0,427397	0,288771	0,324769

Таким образом, для степенной модели и при увеличении заработной платы на 1% от ее среднего значения размер пенсий увеличивается на 0,3867% от своего среднего значения. При гиперболической, полулогарифмической, обратной и экспоненциальной моделях увеличение размера пенсий составляет 0,3885%, 0,4274%, 0,2888% и 0,3248% соответственно.

5. Определим среднюю ошибку аппроксимации:

Она вычисляется по формуле:

вычисления представлены в приложении 7, а итоговые значения в таблице 4.

Таблица 4

Средние ошибки аппроксимации

Модель	Степенная	Гиперболическая	Полулогарифмическая	Обратная	Экспоненциальная
Значение	0,055	0,076	0,065	0,047	0,048

Средняя ошибка аппроксимации не должна превышать 8-10%. В данных моделях она не превышает эту величину. Следовательно, исследуемые данные близки к эмпирическим: модели построены качественно.

6. Оценим статистическую надежность результатов регрессионного моделирования с помощью F-критерия Фишера.

Оценка значимости уравнения регрессии в целом производится на основании F-критерия Фишера. Величина F-критерия связана с индексом детерминации и ее можно рассчитать по следующей формуле:

Фактическое значение величины F-критерия Фишера приведено в таблице 5 для каждой исследуемых моделей.

Таблица 5

Величина F-критерия Фишера

Модель	Степенная	Гиперболическая	Полулогарифмическая	Обратная	Экспоненциальная
Значение	225,4844	112,1281	195,0802	223,4022	266,7377

Табличное значение F(0,05;1;77) = 3,97. Так как для каждой из модели 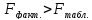, то признается статистическая значимость уравнений в целом.

Вывод

В данной работе была определена регрессия пенсий на заработную плату за 2006 год. Для описания регрессии были построены 4 модели: степенная, экспоненциальная, полулогарифмическая, и гиперболическая. Сравним построенные модели по показателям детерминации и средней ошибке аппроксимации, включая данные по линейной модели, взятым из лабораторной работы №1. Данные представлены в таблице 6.

Таблица 6

Сравнение моделей уравнений парных регрессий

Модель	Показатель детерминации	Средняя ошибка аппроксимации
Степенная	0,7454	0,055
Гиперболическая	0,5929	0,076
Полулогарифмическая	0,7170	0,065
Экспоненциальная	0,7760	0,048
Обратная	0,7437	0,047
Линейная	0,7791	0,051

Наиболее хорошо исходные данные аппроксимирует обратная модель, однако и другие модели не превышают уровня 8-10%. Следовательно, каждую из приведенных, можно считать построенной качественно. Индекс детерминации характеризует долю дисперсии, объясненную моделью. У обратной модели этот показатель равен 0,7437. Он показывает, что уравнение регрессии объясняется на 74,37% дисперсией результативного признака, на долю же прочих факторов приходится 25,63%. Однако, у линейной модели этот показатель равен 0,7791. Следовательно, наиболее приемлемыми моделями для данной регрессии будут: линейная и обратная. Так как линейная модель строится проще, то стоит выбрать ее для описания данной регрессии.