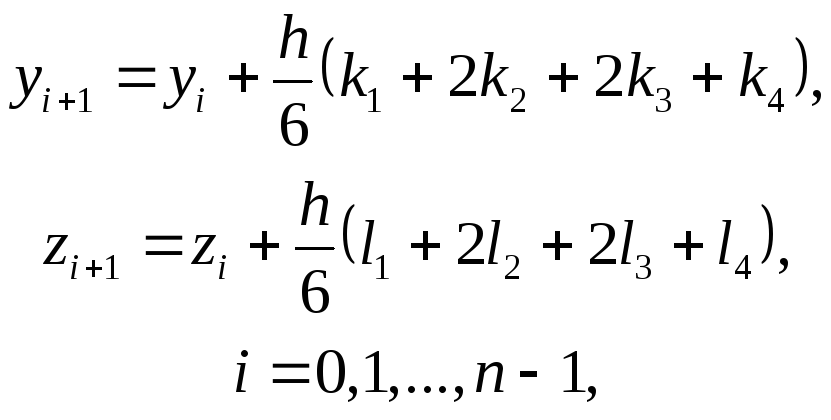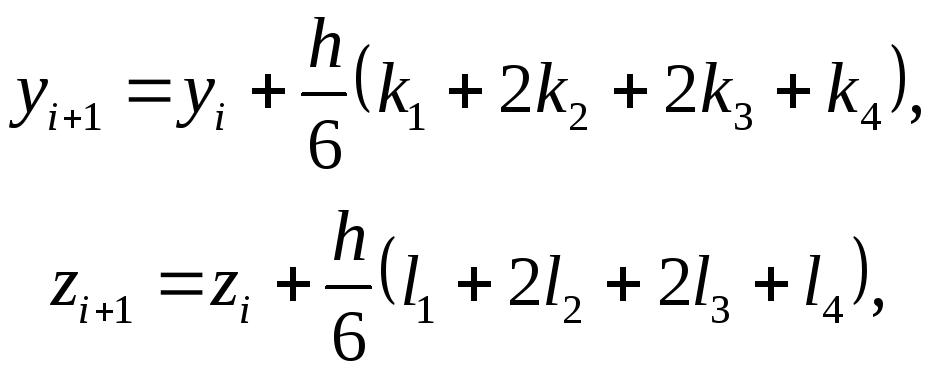7.8. Засоби середовища matlab розв’язування задачі Коші для звичайних диференціальних рівнянь першого порядку з використанням багатокрокових методів
В MATLAB розв’язування задачі Коші для звичайних диференціальних рівнянь першого порядку багатокроковими методами здійснюється за допомогою наступних функцій:
-
ode113 – реалізує багатокроковий метод Адамса-Бешфорса-Маултона змінного порядку;
-
ode15s – реалізує багатокроковий метод змінного порядку (від 1 до 5 по замовчуванню).
Звернення до функцій ode113 та ode15s, а також їх вхідні та вихідні параметри аналогічні функціям ode23 та ode45, які були розглянуті вище.
Слід зазначити, що всі функції MATLAB розв’язування задачі Коші для звичайних диференціальних рівнянь першого порядку можуть також застосовуватись для отримання розв’язку систем цих рівнянь.
7.9. Чисельні методи розв’язування задачі Коші для систем звичайних диференціальних рівнянь першого порядку
Всі розглянуті чисельні методи розв’язування задачі Коші для звичайних диференціальних рівнянь першого порядку легко переносяться на випадок систем таких рівнянь.
Розглянемо задачу Коші для системи звичайних диференціальних рівнянь першого порядку
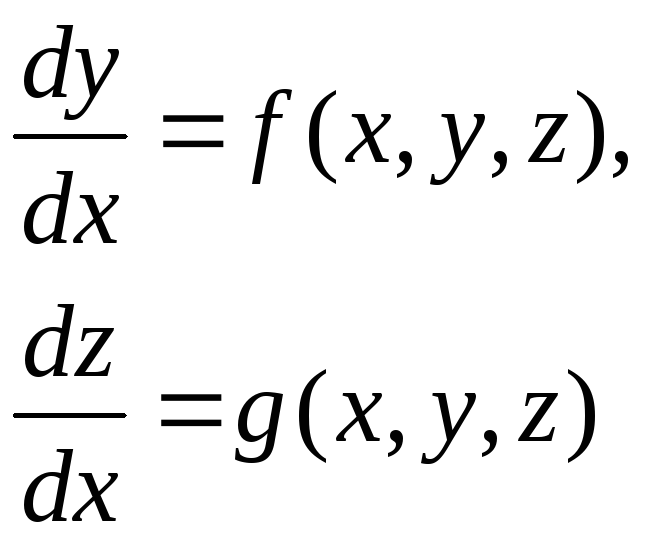(7.52)
з початковими умовами
(7.53)
Якщо на проміжку
функції
та
задовольняють теорему Пікара, то задача
(7.52)-(7.53) має єдиний розв’язок.
Нехай на проміжку
задана система розрахункових вузлів
,
де
,
– крок.
Аналогічно випадку одного диференціального рівняння, можна вивести формули методу Ейлера для розв’язування задачі Коші (7.52)-(7.53):
(7.54)
,
де
,
.
Метод Рунге-Кутта четвертого порядку для задачі (7.52)-(7.53) виражається формулами:
|
|
(7.55) |
де
|
|
(7.56) |
,
,
,
.
Аналогічно можна
узагальнити ці та інші однокрокові й
багатокрокові методи на випадок
розв’язування задачі Коші для систем
звичайних диференціальних рівнянь
першого порядку з
рівняннями.
7.10. Чисельні методи розв’язування задачі Коші для звичайних диференціальних рівнянь вищих порядків
При розв’язуванні задачі Коші для звичайних диференціальних рівнянь вищих порядків, ці рівняння зводяться до систем рівнянь першого порядку. Для знаходження розв’язку такої системи можна використовувати будь-які з розглянутих вище чисельних методів.
Розглянемо даний підхід на прикладі задачі Коші для звичайного диференціального рівняння другого порядку:
, (7.57)
,
. (7.58)
Введемо заміну
.
Тоді замість задачі (7.57)-(7.58) для
диференціального рівняння другого
порядку отримаємо задачу Коші для
системи диференціальних рівнянь першого
порядку:
(7.59)
з початковими умовами
(7.60)
Тепер для
розв’язування задачі Коші (7.59)-(7.60) на
проміжку
можна використовувати, наприклад,
методи, розглянуті в попередньому
пункті.
Метод Ейлера:
(7.61)
.
Тут
,
,
,
,
.
Тоді розв’язком
задачі (7.57)-(7.58) будуть значення
,
знайдені в результаті застосування
формул (7.61).
Метод Рунге-Кутта четвертого порядку:
|
|
(7.62) |
де
|
|
(7.63) |
,
,
,
.Треба зазначити, що розроблені також й інші спеціальні методи, призначені для розв’язування задачі Коші для звичайних диференціальних рівнянь вищих порядків.