
- •Уравнения и неравенства, содержащие переменную под знаком модуля
- •1. Определение и свойства модуля действительного числа
- •2. Методы решения уравнений, содержащих переменную под знаком модуля
- •3. Методы решения неравенств, содержащих переменную под знаком модуля
- •4. Уравнения и неравенства с параметрами
- •5. Задачи для самостоятельного решения
Уравнения и неравенства, содержащие переменную под знаком модуля
1. Определение и свойства модуля действительного числа
Модулем действительного числа а
называется число
![]() ,
равное самому числу а, если оно
неотрицательное и противоположному
для а числу, если оно отрицательно.
,
равное самому числу а, если оно
неотрицательное и противоположному
для а числу, если оно отрицательно.
Таким образом, по определению имеем:
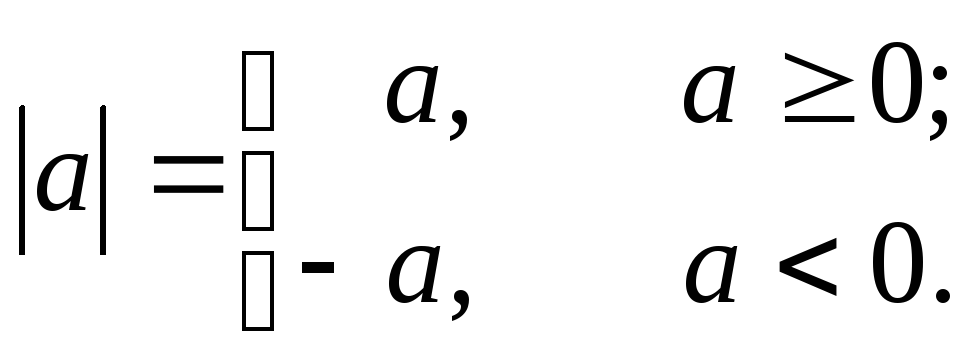
Свойства модуля действительного числа:
-
 ;
5)
;
5)
 ,
,
 ;
; -
 ;
6)
;
6)
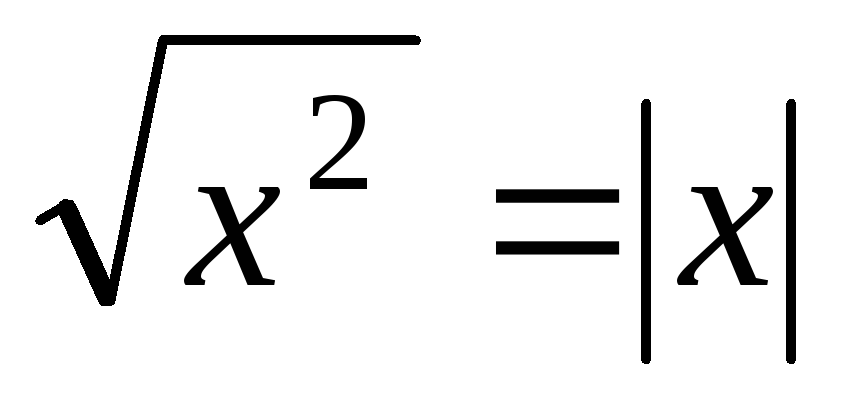
-
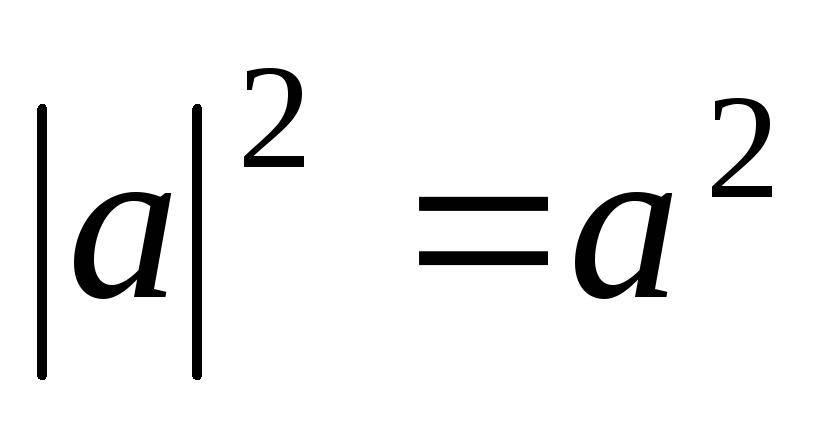 ;
7)
;
7)
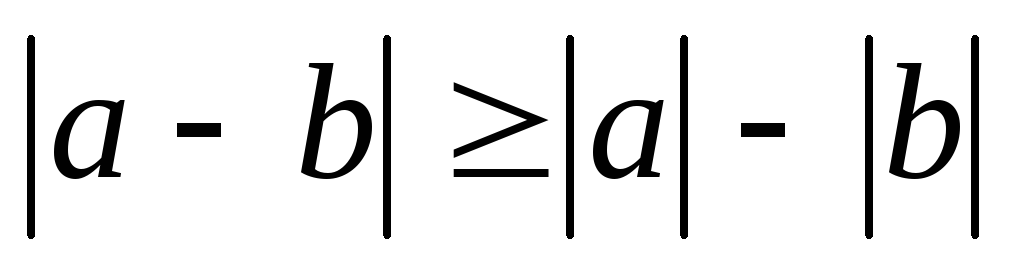 ;
; -
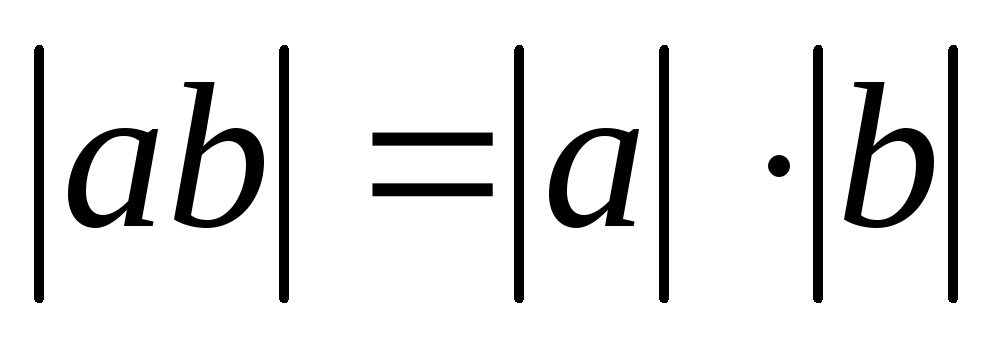 ;
8)
;
8)
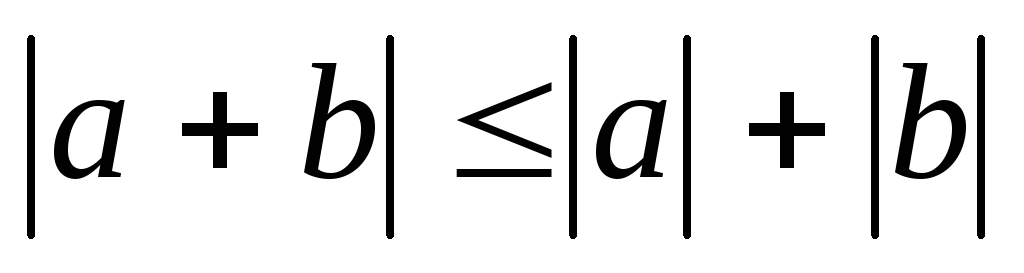 .
.
Геометрический смысл модуля действительного числа:
Известно, что любое действительное
число а можно интерпретировать, как
точку на числовой оси. В связи с этим
геометрически
![]() - это расстояние от начала координат до
точки а. При этом величина
- это расстояние от начала координат до
точки а. При этом величина
![]() задает расстояние между точками а и
b на числовой оси.
задает расстояние между точками а и
b на числовой оси.
2. Методы решения уравнений, содержащих переменную под знаком модуля
При решении уравнений, содержащих переменную под знаком модуля, могут быть использованы следующие методы:
-
раскрытие модуля по определению;
-
возведение обеих частей уравнения в квадрат;
-
разбиение области решения уравнения на промежутки знакопостоянства выражений, стоящих под знаком модуля.
Каждый из этих методов рассмотрим на конкретном примере и сделаем необходимые обобщения.
Пример 1. Решить уравнение
![]() .
.
Решение. 1-й способ. Воспользовавшись
определением модуля получим совокупность
двух систем: 1)
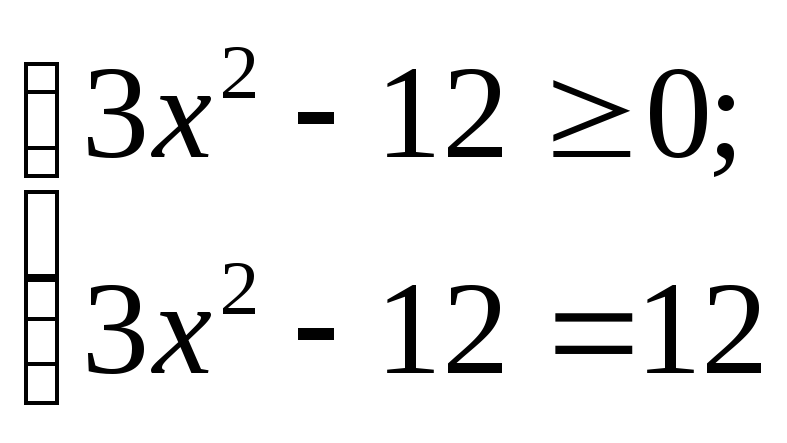 или 2)
или 2)
 .
Решим каждую из этих систем: 1)
.
Решим каждую из этих систем: 1)

![]()
![]() ;
2)
;
2)
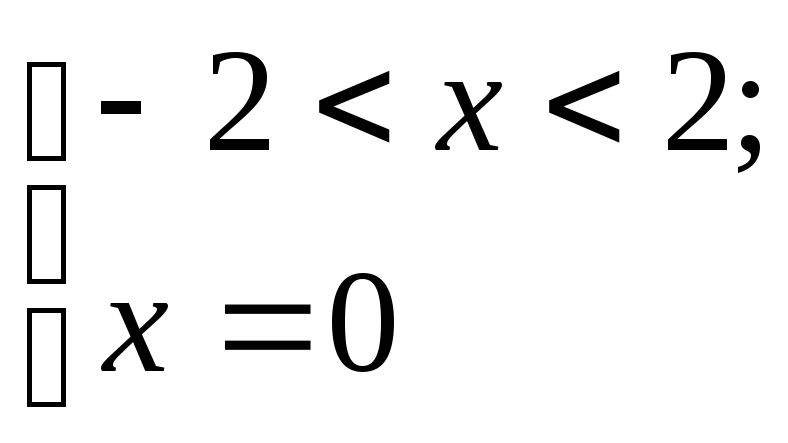
![]() х = 0.
х = 0.
Ответ: х1 = 0;
![]() .
.
2-й способ. Так как обе части уравнения
неотрицательны, то возведя их в квадрат,
получим уравнение равносильное данному:
![]() ,
учитывая свойство 3, будем иметь:
,
учитывая свойство 3, будем иметь:
![]()
![]()
![]()
![]()
![]()
![]() х1 = 0;
х1 = 0;
![]() .
.
Пример 2. Решить уравнение
![]()
Решение. 1-й способ. Уединим
выражение, содержащее знак абсолютной
величины
![]() .
Воспользовавшись определением модуля
получим совокупность двух систем: 1)
.
Воспользовавшись определением модуля
получим совокупность двух систем: 1)
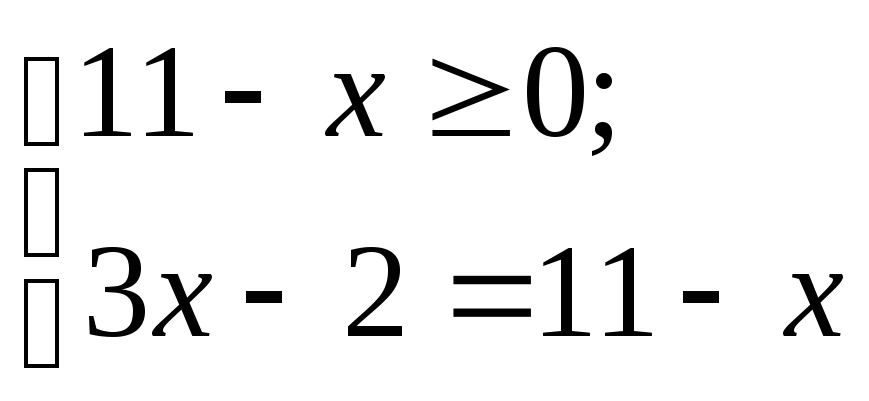 ; 2)
; 2)
 .
Решив полученные системы найдем корни
первоначального уравнения:
.
Решив полученные системы найдем корни
первоначального уравнения:
![]() ;
;
![]() .
.
2-й способ. Возведем обе части
уравнения
![]() в квадрат, потребовав при этом, чтобы
в квадрат, потребовав при этом, чтобы
![]() .
Получим систему:
.
Получим систему:
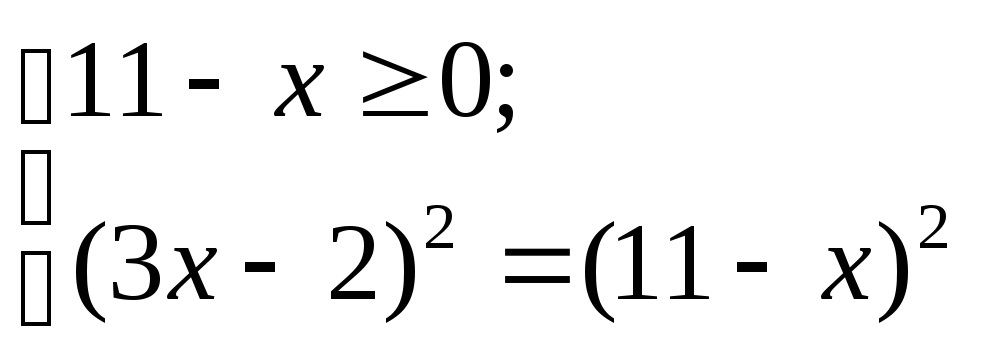 .
Решая полученную систему, получим те
же корни.
.
Решая полученную систему, получим те
же корни.
Ответ:
![]() ;
;
![]() .
.
Решение уравнений вида
![]()
Уравнение вида
![]() может быть решено двумя методами:
может быть решено двумя методами:
-
по определению модуля оно равносильно совокупности двух уравнений:
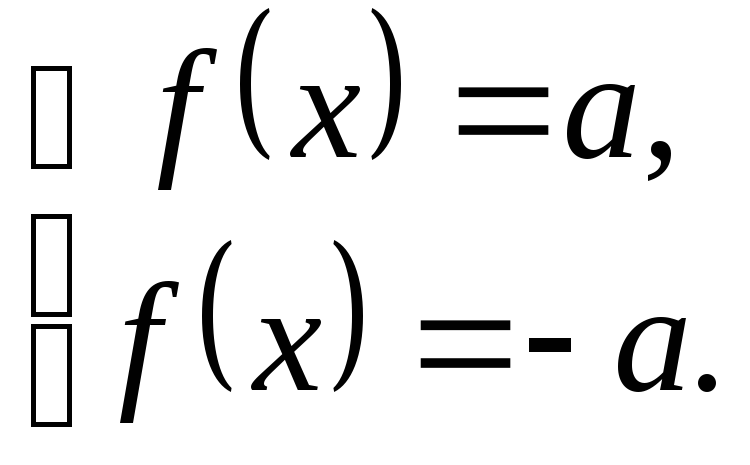
-
возведением обеих частей уравнений в квадрат. Учитывая свойство 3, получится уравнение
 ,
равносильное данному.
,
равносильное данному.
Решение уравнений вида
![]()
Уравнение вида
![]() может быть решено двумя методами:
может быть решено двумя методами:
-
по определению модуля оно равносильно совокупности двух систем:
1)
![]() ; 2)
; 2)
![]()
-
возведением обеих частей уравнений в квадрат. Учитывая, что правая часть уравнения должна быть неотрицательной, получится система:
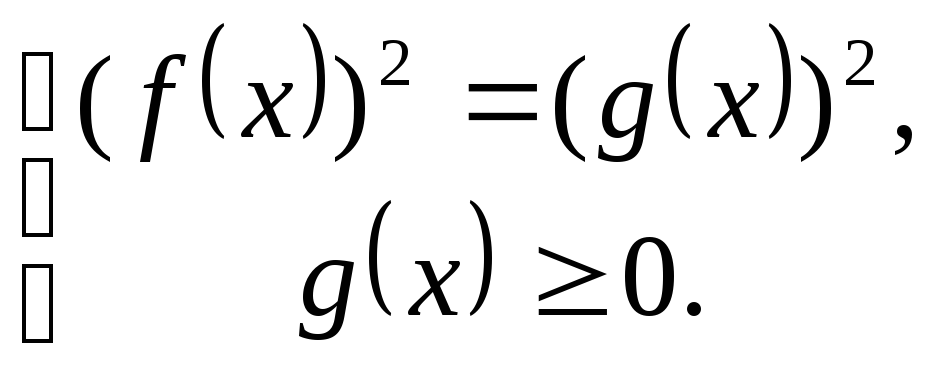
Пример 3. Решить уравнение
![]()
Решение. Обе части уравнения неотрицательны, поэтому, возведя их в квадрат и учитывая свойство модуля 3, получим уравнение равносильное данному:
![]()
Раскрыв скобки и приведя подобные члены,
получим квадратное уравнение:
![]() ,
решив которое найдем корни первоначального
уравнения:
,
решив которое найдем корни первоначального
уравнения:
![]() ;
;
![]() .
.
Ответ:
![]() ;
;
![]() .
.
Решение уравнений вида
![]()
Уравнения вида
![]() удобно решать методом возведения
обеих частей в квадрат, если f(x)
и g(x)
- многочлены первой степени.
удобно решать методом возведения
обеих частей в квадрат, если f(x)
и g(x)
- многочлены первой степени.
Пример 4. Решить уравнение
![]()
Решение.
1. Найдем значения переменной, обращающие
выражения, стоящие под знаком абсолютной
величины в нуль:
![]() ;
;
![]() ;
;
![]() .
.
2. Нанесем полученные значения на числовую прямую и на каждом из полученных интервалов определим знак каждого выражения, стоящего под знаком абсолютной величины:
 х : – –
– +
х : – –
– +
х + 1: – – + +
х + 2: – + + +
3. Пользуясь определением модуля и используя п. 2 раскроем на каждом из интервалов все знаки модулей:
при
![]() имеем:
имеем:
![]() ;
;
при
![]() имеем:
имеем:
![]() ;
;
при
![]() имеем:
имеем:
![]() ;
;
при
![]() имеем:
имеем:
![]() .
.
4. Решим каждое из полученных уравнений:
при
![]() :
х = –2 это значение в интервал не
входит; при
:
х = –2 это значение в интервал не
входит; при
![]() :
х = –2 полученное значение входит
в обозначенный интервал; при
:
х = –2 полученное значение входит
в обозначенный интервал; при
![]() :
ни при каких значениях х уравнение
решений не имеет; при
:
ни при каких значениях х уравнение
решений не имеет; при
![]() :
х = –2 в данный интервал это значение
не входит.
:
х = –2 в данный интервал это значение
не входит.
5. Таким образом, уравнение имеет единственный корень х = –2, так как это значение входит в один из интервалов.
Ответ: х = –2.
Алгоритм, с помощью которого было решено уравнение, можно обобщить для решения любого уравнения, содержащего несколько модулей:
-
Найти значения переменной, обращающие выражения, стоящие под знаком абсолютной величины в нуль;
-
Все найденные значения нанести на числовую прямую и на каждом из полученных интервалов определить знак каждого выражения, стоящего под знаком абсолютной величины;
-
Учитывая получившиеся знаки, воспользоваться определением модуля и раскрыть на каждом из интервалов все знаки модулей;
-
Решить каждое из полученных уравнений и из их решений выбрать те, которые принадлежат соответствующему интервалу, они и будут являться решениями первоначального уравнения.
Пример 5. Решить уравнение
![]() .
.
Решение. Заметим, что слагаемые в знаменателе неотрицательны, следовательно сумма равна нулю в том и только в том случае, когда оба слагаемых одновременно равны нулю. Ни при каких значениях переменной этого произойти не может, т.е. знаменатель дроби при любом значении х отличен от нуля.
Для решения воспользуемся сформулированным алгоритмом.
1.
![]()
![]()
![]() ;
;
![]()
![]()
![]() .
.
2.
![]() + – + +
+ – + +
![]() – – – +
– – – +

3. При
![]() имеем:
имеем:
![]()
![]()
![]() ;
;
При
![]() имеем
имеем
![]()
![]()
![]() ;
;
![]() ;
;
При
![]() имеем:
имеем:
![]()
![]()
![]() ;
;
При
![]() имеем:
имеем:
![]()
![]()
![]() .
.
4. Выбирая из полученных решений те,
которые принадлежат соответствующим
промежуткам, получим:
![]() ;
;
![]() ;
;
![]() .
.
Ответ:
![]() ;
;
![]() ;
;
![]() .
.
