Сборочный чертеж спецификация

В зависимости от содержания изображения разделяют на виды, разрезы, сечения, и их количество должно быть минимальным, но достаточным для полного представления о предмете.

Приступая к штриховке разрезов, надо учитывать, что одна и та же деталь на всех изображениях заштриховывается в одну сторону и с одинаковой разрядкой. Для металлов используется односторонняя штриховка, для неметаллов – перекрестная. Штриховку смежных деталей, изготовленных из одного типа материала, выполняют с изменением направления, со сдвигом линий штриховки или с изменением расстояний между ними. Узкие и длинные площади сечений с шириной 2-4 мм. штрихуют отдельными небольшими участками, но обязательно на концах и у контуров отверстий. При ширине рассекаемых деталей меньше двух миллиметров – их зачерняют, оставляя просветы между смежными деталями.

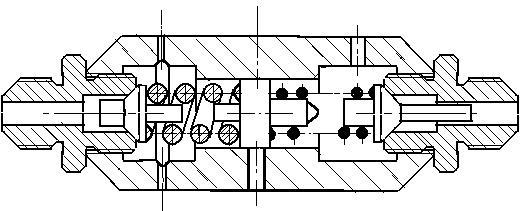
Выполняя на месте основных видов разрезы узла, следует помнить, что так называемые неполые валы, т.е. валы, не имеющие сквозных осевых отверстий, попадая в продольный разрез, изображаются видом. Такие детали в заданиях могут иметь самые разнообразные конкретные названия: шпиндели, штоки, толкатели, клапана, золотники, пуансоны, пробки, рукоятки и т.д. и т.п. Они и на эскизах заданий за редким исключением изображены видом. Если на таких деталях есть углубления различной конфигурации (это могут быть и сквозные, но поперечные отверстия), то они выявляются местным разрезом-выровом. Любые стандартные крепежные изделия: болты, винты, штифты, шпильки, гайки, шайбы – тоже, попадая в продольный разрез, изображаются видом (см. Рис. 1, 4, 7, 8 и др.). Это же касается шариков. Спицы маховиков, тонкие стенки типа ребер жесткости и т.п. в продольном разрезе показывают не заштрихованными (их режут, но не штрихуют).

Пружины (вар. №№3,12,15,19,37,39 и др.). Их на продольном разрезе узла (всегда с правой навивкой) можно изображать видом, «честным» разрезом или только сечениями витков (т.е. используется некая условность). В последнем случае отдельные детали или элементы корпуса, в котором находится пружина, и расположенные за пружиной, показывают лишь с внешней стороны зоны, которая определяется осевыми линиями сечений витков. Это же правило справедливо, когда используется еще одна условность: при числе витков более четырех показывают лишь опорные витки и 1-2 соседних, а по всей длине пружины проводят осевые линии через центры сечений витков (см. Рис.7). Если диаметры окружностей сечений витков пружины меньше двух миллиметров, то их рекомендуется не штриховать, а зачернять. Следует отметить, что на эскизах заданий длины пружин указаны в свободном состоянии. Там же помещены некоторые технические требования, в которых: n- число рабочих витков, n1 - полное число витков; при строгом ограничении размера внутреннего диаметра пружины указаны требования контроля стержнем – Dc; если необходимы ограничения пружины по наружному диаметру, то дается диаметр контрольной гильзы – Dг.

 Рис.7

Подшипники служат опорами для вращающихся деталей механизмов: валов, зубчатых колёс, шкивов и т.д. (вар. №21). На сборочных чертежах их можно изображать различными способами (см. Рис. 8). 

 

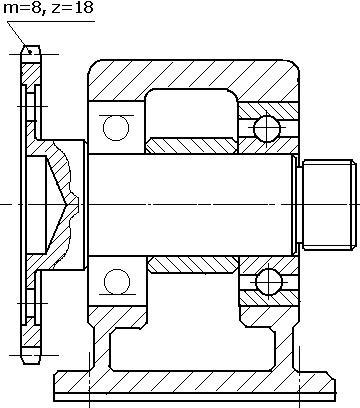
Рис. 8

Обучение специалистов широкого профиля предусматривает глубокое усвоение теоретической базы, овладение фундаментальными основами инженерной и управленческой деятельности, серьезную практическую подготовку. Инженерная графика относится к базовым общеинженерным дисциплинам, освоение которой - необходимое условие углубленного овладения фундаментальными инженерными дисциплинами и эффективного использования компьютерно-графических систем для автоматизации изготовления чертежей. При изучении дисциплин "Основы машинной графики" и "Начертательная геометрия. Инженерная графика" студенты учатся изображать на плоскости различные геометрические фигуры и решать инженерно-геометрические задачи, развивая способность к пространственному представлению и логическому мышлению, без чего невозможно никакое техническое творчество. Кроме того, они знакомятся с основами графических пакетов прикладных программ машинной графики. Приступая к изучению сборочных единиц, студенту следует сразу определиться в терминологии и не путать уже известное понятие - «деталь» и новое – «сборочная единица». Деталь это изделие, изготовленное из единого куска материала. Сборочная единица (узел) – изделие, состоящее из нескольких деталей. Они подлежат соединению между собой на предприятии-изготовителе сборочными операциями (свинчивание, сочленение и т.д.). Для разработки сборочного чертежа и спецификации к нему студент получает печатные методические материалы и индивидуальное задание, состоящее из описания сборки узла и эскизов, входящих в него оригинальных деталей. Форма исполнения упоминаемых в описании стандартных деталей определяется студентом по справочникам и методическим материалам. После этого этапа проверяется и окончательно заполняется спецификация Плоские грани на криволинейных поверхностях полезно выделять диагональными сплошными тонкими линиями. Следует частично показывать насечку или рифление на поверхностях, которые их имею Механические краны (вентили) – выполняются в закрытом положении (клапан сидит на седле)

Современные чертежи и процесс их выполнения постоянно совершенствуется. С развитием техники, с появлением компьютеров труд чертёжника очень изменился. Однако в основе графических изображений по-прежнему лежит труд человека, свободно владеющего специфическим языком, называемым языком техники. 

Лекция №6-2

ПЕРЕСЕЧЕНИЕ ПЛОСКОСТИ С МНОГОГРАННИКОМ

Построение сечения многогранника требует многократного решения задачи о нахождении точки пересечении прямой с плоскостью. Точки, в которых ребра многогранника пересекаются с заданной плоскостью, будут вершинами искомого сечения.

Тот же результат можно получить, сведя задачу к построению прямых пересечения плоскости с гранями тела.

Дана призма и плоскость общего положения заданная двумя пересекающимися прямыми а и в (рис.6.11). Необходимо найти  сечение призмы данной плоскостью. Для предупреждения самоотвинчивания болтов, винтов и гаек от вибрации и толчков применяют пружинные шайбы

а) модель
б) эпюр
Рисунок 6.11. Пересечение плоскости общего положения с призмой

Решим поставленную задачу нахождением точек пересечения ребер призмы с плоскостью. Для чего, через горизонтальные проекции ребер проведем вспомогательные секущие плоскости α, β и γ.Построив линии пересечения вспомогательных плоскостей с заданной, находим на фронтальной проекции точки пересечения  их с соответствующими ребрами призмы К₂, М₂ и N₂ – вершины фронтальной проекции сечения призмы. По линиям связи находим горизонтальные проекции этих точек. Полученные точки соединяем прямыми линиями, с учетом видимости. При решении вопроса о видимости сторон  построенного сечения следует иметь в виду достаточно очевидное правило: точка и линия, лежащие на поверхности многогранника, видимы только в том случае, если они расположены на видимой грани. Наброски фрагментов интерьера свободной линией Наброски выполняем простым карандашом средней твердости. Суть этого задания в том, чтобы совершенно исключить какие-либо промеры и, разумеется, исправления. Мы просто перечисляем линии конструкции предмета, не заботясь о пропорциях. Рассмотренные свойства проецирования и их свойства решают задачу определения проекции оригинала, но не дают возможности воспроизвести его по одной проекции

 

ПЕРЕСЕЧЕНИЕ ПРЯМОЙ ЛИНИИ С МНОГОГРАННИКОМ

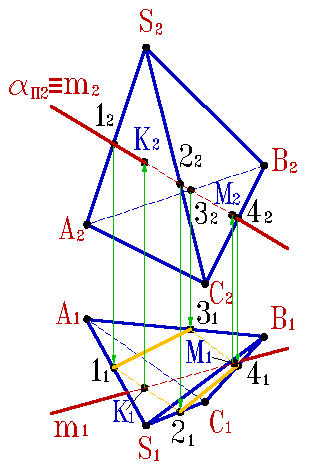
Для определения точек пересечения прямой линии с многогранником, задача сводится к нахождению точек пересечения прямой с плоскостями граней (рис.6.12).

Алгоритм решения задачи: 1. Провести плоскость : m. 2. Построить сечение многогранника плоскостью . Определить искомые точки К,М - пересечения  полученного сечения с прямой m.
	а) модель		б) эпюр
Рисунок 6.12. Пересечение прямой линии с пирамидой

ВЗАИМНОЕ ПЕРЕСЕЧЕНИЕ МНОГОГРАННИКОВ

Построение линии взаимного пересечения многогранных поверхностей можно производить двумя способами, комбинируя их между собой или выбирая из них тот, который в зависимости от условий задания дает более простые построения. Эти способы следующие:

1.Определяют точки, в которых ребра одной из многогранных поверхностей пересекают грани другой и ребра второй пересекают грани первой (задача на пересечение прямой с плоскостью). Через найденные точки в определенной последовательности проводят ломаную линию, представляющую собой линию пересечения данных многогранников. При этом можно соединять прямыми проекции лишь тех точек, полученных в процессе построения, которые лежат в одной и той же грани.

2. Определяют отрезки прямых, по которым грани одной поверхности пересекают грани другой (задача на пересечение двух плоскостей между собой); эти отрезки являются звеньями ломаной линии, получаемой при пересечении  многогранных поверхностей.

Если проекция ребра одной из поверхностей не пересекает проекции грани другой хотя бы на одной из проекций, то данное ребро не пересекает этой грани. Однако пересечение проекций ребра и грани еще не означает, что ребро и грань пересекаются в пространстве.
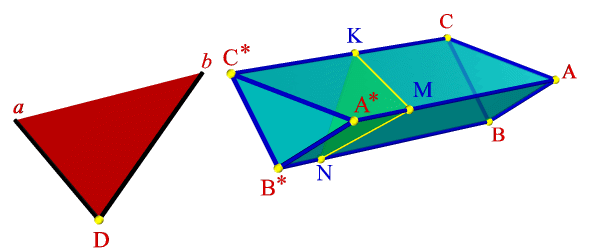
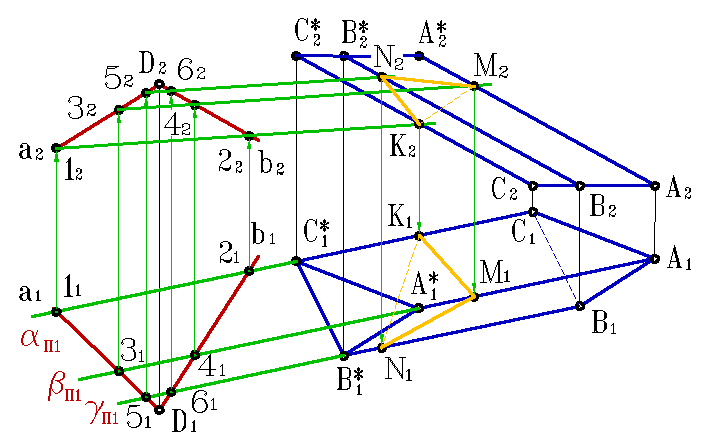
а) модель	б) эпюр
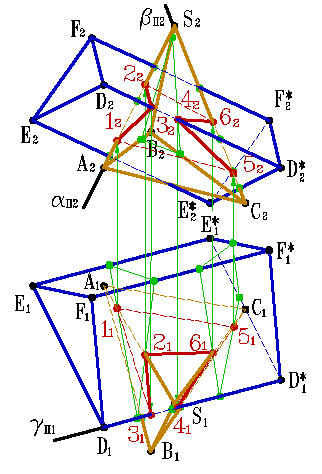
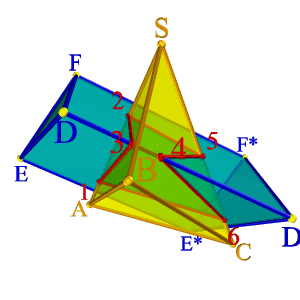
Рисунок 6.13. Пересечение пирамиды с призмой

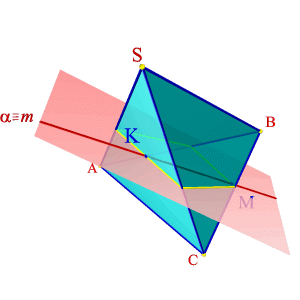
    На примере (рис.6.13) показано пересечение поверхности треугольной призмы с треугольной пирамидой. Построение основано на нахождении точек пересечения ребер одного многогранника с гранями другого. На рисунке 6.13 б показано построение линии пересечения пирамиды АВСS и треугольной призмы DEFD*E*F*. 

Для нахождения точек 1 и 2 в которых ребро пирамиды AS пересекает грани DD*EE* и EE*FF* призмы, через проекцию ребра A₂S₂ проведена фронтально проецирующая плоскость α_П2, которая пересекает ребра призмы в  трех точках, горизонтальные проекции  этих точек пересечения плоскости α с ребрами призмы, образуют треугольник. Проекция ребра пирамиды  A₁S₁ пересекает полученный треугольник в точках 1₁ и 2₁.

С помощью фронтально - проецирующей плоскости β, находим точки 5 и 6  пересечения ребра пирамиды  SC с гранями призмы EE*FF* и EE*DD*, а при помощи горизонтально проецирующей плоскости γ находим точки 3 и 4 пересечения ребра призмы с гранями пирамиды. Соединив полученные точки, с учетом видимости, получим пространственную ломаную линию – линию пересечения данных многогранников.

Лекция №7-1

 

 

КРИВЫЕ ЛИНИИ

 

Кривая линия - это множество точек пространства, координаты которых являются функциями одной переменной. Термин «кривая» в разных разделах математики определяется по-разному. В начертательной геометрии кривую рассматривают как траекторию, описанную движущей точкой, как проекцию другой кривой, как линию пересечения двух поверхностей, как множество точек, обладающих каким-либо общим для всех их свойством и т.д. Размеры проточек для наружной метрической резьбы

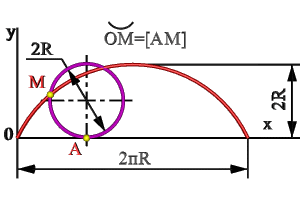
Рисунок 7.1 Циклоида

Например, (рис.7.1) циклоида – траектория движения точки окружности, катящейся без скольжения по прямой линии. Эта кривая состоит их ряда «арок», каждая из которых соответствует полному обороту окружности. Кривые линии, все точки которых принадлежат одной плоскости, называются плоскими, остальные пространственными. Каждая кривая включает в себя геометрические элементы, которые составляют еёопределитель, т.е. совокупность независимых условий, однозначно определяющих эту кривую.Интерьер в сферической проекции Сферические искажения можно наблюдать на сферических зеркальных поверхностях. Например, на елочных украшениях в виде шаров

Различны и способы задания кривых:

Аналитический – кривая задана математическим уравнением;

Графический – кривая задана визуально на носителе графической информации;

Табличный – кривая задана координатами последовательного ряда точек. 4.4 Подбери своему дому кровлю: мягкая черепица.

Уравнением кривой линии называется такое соотношение между переменными, которому удовлетворяют координаты точки, принадлежащей кривой. Изображение прямых, плоскостей имногогранников

В основу классификации кривых положена природа их уравнений.

Кривые подразделяются на алгебраические и трансцендентные в зависимости от того, являются ли их уравнения алгебраическими или трансцендентными в прямоугольной системе координат.

Плоская кривая линия называется алгебраической, если её уравнение f (xy)=0. Функция  f (xy) является степенным множителем относительно переменных х и у; в остальных случаях кривая называется трансцендентной.

Кривая линия, представленная в декартовых координатах уравнением п- й степени, называется алгебраической кривой п-го порядка.

Порядок плоской алгебраической кривой линии определяется наибольшим числом точек её пересечения прямой линией. Любая прямая линия может пересекать алгебраическую кривую линию п-го порядка не более чем в п точках. 

Рассмотрим несколько примеров алгебраической кривой линии:

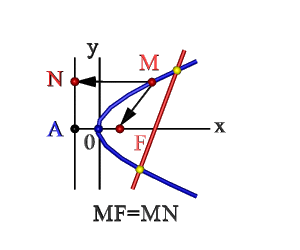
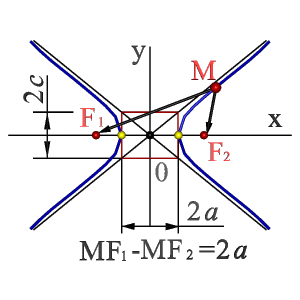
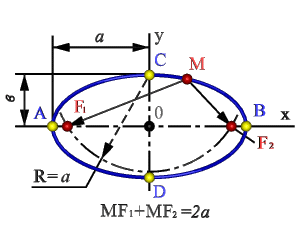
Рисунок 7.2.  Парабола	1. Парабола – кривая второго порядка, прямая пересекает ее в двух точках (рис.7.2). При этомпарабола может быть определена как: -множество точек М(xy) плоскости, расстояние FM которых до определенной точки F этой плоскости (фокуса параболы) равно расстоянию MN до определенной прямой АN - директрисы параболы; -линия пересечения прямого кругового конуса плоскостью, не проходящей через вершину конуса и параллельная какой либо касательной плоскости этого конуса; -в прямоугольной системе координат 0ху с началом в вершине параболы и осью 0хнаправленной по оси параболы уравнение параболы имеет так называемый канонический вид  y2=2px, где р (фокальный параметр) - расстояние от фокуса до директрисы. 2. Гипербола : - множество точек М плоскости (рис.7.3) разность (по абсолютной величине) расстояний F1M иF2M которых до двух определенных точек F1 и F2 этой плоскости (фокусов гиперболы) постоянна: F1M - F2M=2а<2с Середина 0 отрезка F1F2 (фокусного расстояния) называется центром гиперболы; - линия пересечения прямого кругового конуса плоскостью, не проходящей через вершину конуса и пересекающая обе его полости; - в прямоугольной системе координат 0ху с началом в центре гиперболы, на оси 0х которой лежат фокусы гиперболы уравнение гиперболы имеет так называемый канонический  х2/а2 - у2/в2=1, в2=с2 - а2, где а и в длинны полуосей гиперболы. 3. Эллипс : - множество точек М плоскости (рис.7.4), сумма расстояний МF1 и МF2 которых до двух определенных точек F1 и F2 (фокусов эллипса) постоянна МF1+МF2=2а. Середина 0 отрезка F1F2 (фокусного расстояния)называется центром эллипса; - линия пересечения прямого кругового конуса плоскостью, не проходящей через вершину конуса и пересекающей все прямолинейные образующие одной полости этого конуса; - в прямоугольной системе координат 0ху с началом в центре эллипса, на оси 0х которой лежат фокусы эллипса уравнение эллипса имеет следующий вид х2/а2+у2/в2=1,  где а и в - длинны большой и малой полуосей эллипса. При а=в фокусы F1 и F2 совпадают и указанное уравнение определяет окружность, которая рассматривается как частный случай эллипса. Рассмотренные плоские кривые линии, получаемые при пересечении поверхности прямого кругового конуса плоскостями, различно расположенными по отношению к оси конуса, называюткривыми конических сечений.
Рисунок 8.3. Гипербола
Рисунок 7.4. Эллипс
Рисунок 7.5. Синусоида

Трансцендентные кривые в отличие от алгебраических могут иметь бесконечное количество точек пересечения с прямой, точек перегиба, вершин и т.п. 

Синусоида - трансцендентная плоская кривая линия (рис.7.5), получающаяся в результате двойного равномерного движения точки - поступательного и возвратно-поступательного в направлении, перпендикулярном первому.

Синусоида - график функции у=sin x, непрерывная кривая линия с периодом Т=2п.

Наряду с этим у трансцендентных кривых могут быть характерные точки, которых не существует у алгебраических кривых: точки прекращения, угловые точки (точки излома), асимптотические точки. Простейшими примерами трансцендентных кривых служат графики функций логарифмической, показательной тригонометрической, а также все спирали, циклоиды и т.п.

Кривая линия как траектория движущейся точки должна быть непрерывной. Движущаяся точка в любом положении должна иметь определенное направление движения. Это направление указывает прямая (касательная), проходящая через рассматриваемую точку.

Длина отрезка кривой линии определяется в общем случае, как сумма длин отрезков вписанной в нее ломаной линии, с заданной точностью передающей форму кривой.

Особый интерес представляют окружность и цилиндрическая винтовая линии, каждая из которых является эталоном соответственно плоских и пространственных кривых линий.

В практике конструирования линий и поверхностей широко  используются обводы. Это кривые, составленные из дуг различных кривых, определенных парами смежных точек. Обводом ряда точек плоскости является плоская кривая, пространства - пространственная. Точки стыка дуг называются узлами. Обвод заданный координатами своих точек называется дискретным. Обвод называется гладким, если дуги обвода в узлах имеют общие касательные.

Рисунок 7.6. Касательные к кривой линии

Плоская кривая а построена в плоскости  (рис.7.6). Через точку А проведены секущие хордыАЕ и АD. Если точку Еприближать к точке А, секущая АЕповорачивается вокруг точки А. Когда точка Е совпадет с точкой А (А≡Е) секущая АЕдостигнет своего предельного положения t. В этом предельном положении секущая называется полукасательной к кривой а в точке А. Секущая АD в предельном положении А≡D также представлена полукасательной t. Кривая линия в точке А имеет две полукасательные прямые, которые совпадают и определяют одну касательную  к кривой линии в точке А – кривая в этой точке называется плавной. Кривая плавная во всех её точках называется плавной кривой линией. Нормалью п  в точке А кривой линии называется перпендикуляр к касательной.

На кривой линии могут быть точки где разнонаправленные полукасательные не принадлежат одной прямой, а составляют между собой угол. Так на кривой а в точке В угол δмежду полукасательными не равен 180⁰. Точка В в этом случае называется точкой излома или выпадающей точкой.

Рисунок 7.7. Кривая линия как  траектория движения точки

Плоскую кривую линию можно рассматривать как траекторию движения точки в плоскости (рис.8.7); точка движется по касательной к кривой линии, обкатывая эту кривую без скольжения. Движение точки вдоль кривой а связано с непрерывным изменением двух величин: расстояния S, на которое удалена точка от начального положения и угла α  поворота касательной  относительно начального положения. Если с увеличением пути  S непрерывно увеличивается и α, кривая называется простой. Угол α (угол смежности) между касательными в двух бесконечно близких точках кривой, отнесенный к длине дуги между этими точками, определяет степень искривленности кривой линии, т.е. определяет кривизнукривой.

, предел отношения угла смежности касательных к соответствующей дуге.

Рисунок 7.8. Кривизна кривой

Кривизна прямой в любой её точке равна нулю. Кривизна произвольной кривой линии в различных точках различна, в отдельных точках она может быть равна нулю. Такие точки называются точками спрямления. Кривизна в каждой из точек плоской кривой а определяется с помощью соприкасающейся в этой точке окружности (рис.7.8). Соприкасающейся окружностью или кругом кривизны в данной точке называется предельное положение окружности, когда она проходит через данную точку и две другие бесконечно близкие к ней точки. Центр соприкасающейся окружности называется центром кривизны кривой в данной точке, а радиус такой окружности – радиусом кривизны кривой линии в данной точке. Множество центров кривизны кривой является кривая линия- её называют эволютой данной кривой, а кривая по отношению к своей эволюте называется эвольвентой.

Лекция №7-2

 

СВОЙСТВА ОРТОГОНАЛЬНЫХ ПРОЕКЦИЙ КРИВОЙ ЛИНИИ

1. Проекцией кривой линии является кривая линия;

2. Касательная к кривой линии проецируется в касательную к её проекции;

3. Несобственная точка кривой проецируется в несобственную точку её проекции;

4. Порядок линии – проекции алгебраической кривой равен порядку самой кривой или меньше;

5. Число узловых точек ( в которых кривая пересекает сама себя) проекции равно числу узловых точек самой кривой.

Случаи когда, плоская кривая проецируется в прямую (свойства 1,4,5), а касательная в точку (свойство 2) не учитываются. Трапецеидальная резьба относится к кинематическим резьбам и предназначена для передачи движения. ГОСТ 9484—81 устанавливает профиль и размеры его элементов. Профиль трапецеидальной резьбы — равнобочная трапеция с углом 30° между ее боковыми сторонами Рисунок головы Мастерская живописи и рисунка История искусства Проецируещие прямые Прямые перпендикулярные к какой-либо координатной плоскости называются проецирующими прямыми. Они делятся на горизонтально-проецирующие, фронтально-конкурирующие, профильно-проецирующие.

ПРОСТРАНСТВЕННЫЕ КРИВЫЕ ЛИНИИ

Пространственные кривые линии в начертательной геометрии обычно рассматриваются как результат пересечения поверхностей или траекторию движения точки.

Пространственную, так же как и плоскую, кривую линию на чертеже задают последовательным рядом точек. коляски детские, доставка

Классическим примером пространственных кривых линий являются цилиндрическая и коническая винтовые линии.