5.5. Дискретизация и комбинирование внешних состояний

Пусть некоторый параметр внешнего состояния влияет на свойства системы или процесса и по условиям задачи ограничен пределами . Из этого интервала следует выбрать пред­ставительные значения , так, чтобы решаемая за­дача описывалась достаточно точно, но чтобы в интересах упрощения расчетов было как можно меньше. Эти два требова­ния явно противоречивы. Предельно простыми расчеты стано­вятся, когда весь интервал представляется единственным зна­чением , что соответствует детерминированной оптимиза­ции. Аналогично можно говорить о квазидетерминированных оптимизационных расчетах в случаях, когда представительные значения переменных из интервала не рассматривают­ся как неизвестные (неважно, на каком основании). Например, использование неопределенных величин часто не предусмотре­но нормами, или же затраты, которые мы можем себе позво­лить, предопределяют выбор представительных значений. Зада­ние параметров в этом случае осуществляется однозначно и не является случайным. Обыкновенно используют среднее , а также крайние и значения. Если различные возможные состояния параметра представляют многими зна­чениями , то целесообразно исходить из равномер­ного разделения диапазона изменения параметра, а в качестве представительных значений выбирают середины интервалов (рис. 5.11). Непосредственное влияние предельных значений и проявляется тогда только с ростом .

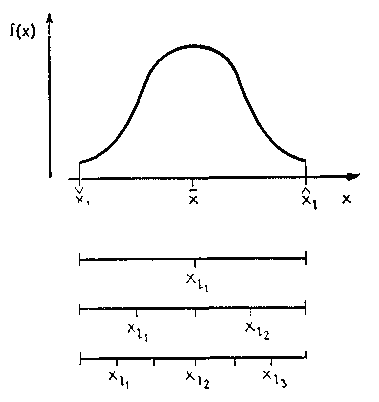
Рис. 5.11. Выбор дискретных реа­лизаций

Желаемая формулировка задачи получается из комбинации выбранных представительных значений, которые должны адек­ватно характеризовать анализируемый параметр внешнего со­стояния.

Кроме снижения затрат на обработку, имеются и другие ос­нования, которые заставляют делать число выбранных предста­вительных значений как можно меньше. Исследователь стре­мится из осторожности сделать диапазон столь большим, что­бы гарантированно охватить все реализации анализируемого параметра внешнего состояния. Однако краевые области интервалов, по всей вероятности, содержат меньше представительных значений, чем центральные. Ясно, что параметр будет оценен тем лучше, чем больше число выбранных реализаций.

5.5.1. Разделение общего числа представительных значений по параметрам внешнего состояния

Чем больше общее число параметров исходной информа­ции, которые приходится учитывать и комбинировать, тем боль­ше возрастают, естественно, и расходы, а число всех комби­наций, в соответствии с формулой (6.1), составляет

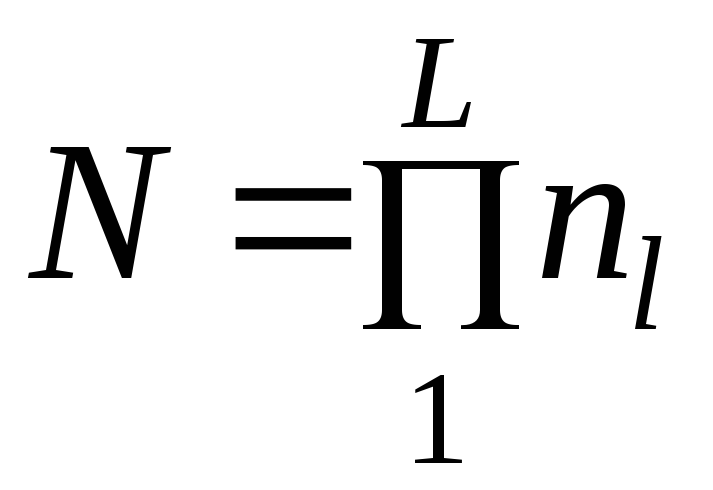
где – число состояний -го параметра исходных данных. По­скольку число принимаемых в расчет внешних состояний для многих ситуаций принятия решения предопределяется затрата­ми на обработку, из множества всех возможных следует вы­брать такие сочетания, которые наилучшим образом характери­зовали бы состояние исходных данных и его изменения.

Этот отбор должен, насколько возможно, удовлетворять сле­дующим требованиям: 1) число значений параметра долж­но соответствовать его влиянию на результат; 2) сочетания зна­чений параметра , которые оказывают одинаковое или сходное влияние на результат, не должны быть представлены в со­стояниях многократно; 3) отбор должен быть в максимальной степени независимым от субъективного отношения исследовате­ля; 4) те из выбранных сочетаний, которые по характеру ре­шаемой задачи маловероятны, должны быть исключены.

Хотя субъективное влияние исследователя часто очень вели­ко, сам по себе субъективный отбор широко укоренился в прак­тике и достаточно надежен. Все требования, кроме третьего, могут быть в достаточной мере рационально выполнены при субъективном отборе. Рассмотрим три формали­зованных метода, которые, правда, трудоемки, однако они лишь в очень незначительной степени связаны с субъективными-факторами.

Для множества значений параметров , рас­сматривается параллелепипед или другая соответствующая -мерная область. В первом методе в эту область вносятся сфер одинакового и максимально возможного диаметра. Центры сфер определяют, например, на границе параллелепи­педа, подлежащие выбору реализации и одновременно со­четания исходных данных. Этот метод применим только для небольшого числа неопределенных параметров, примерно до . Кроме того, для этой задачи еще не существует общего решения.

По второму методу внутри выбранной области располагают равномерную сетку. На этой сетке выбирают заданное число узловых точек таким образом, чтобы расстояние их друг от друга было максимальным. Для отбора применяют теорию ли­нейных кодов.

Третий метод формального отбора основан на использова­нии метода Монте-Карло и метода классификации. По задан­ным каким-либо образом распределениям определяют стати­стически большое число точек в области неопределенности па­раметра . Полученное множество точек разделяют на групп. Групповые «центры» выбирают при этом так, чтобы средне-квадратическое расстояние между точками в группе было ми­нимальным, а расстояния между центрами – максимальным.

Отметим, что Беляев отдает предпочте­ние второму методу. Эти три формализованных метода распо­лагают представительные значения равномерно, что противо­речит первому требованию отбора.

Число групп некоторого параметра полагают пропор­циональным его значимости .

. (5.13)

Здесь – коэффициент пропорциональности, который даль­ше точно не определяется. В соответствии с формулой (6.8) из разд. 6.2 для рассматриваемого параметра 10 справедливо ра­венство:

. (5.14)

Однако энтропия сама зависит от числа групп. Чтобы представить эту зависимость, функции распределения следует ограничить конечной областью, поскольку в противном случае число групп независимо от ширины интервала становится бесконечно большим.

Пусть все распределения вероятностей сосредоточены на ко­нечных областях шириной и пусть ширина интервала группы для всех параметров постоянна, одинакова и равна , так что

. (5.15)

Определение ширины получается из предположения о нор­мальном распределении. Если обрезать это распределение на границах с обеих сторон, то в этих границах будет заключе­но 99,73 % всех возможных вероятностных событий. Логично и в отношении всех рассматриваемых нами распределений при­нять для область внутри границ . Для трех важных типов распределений это дает следующие результаты.

а) Нормальное распределение:

, (5.16)

, (5.17)

где – параметр нормального распределения.

б) Распределение Вейбулла:

, (5.18)

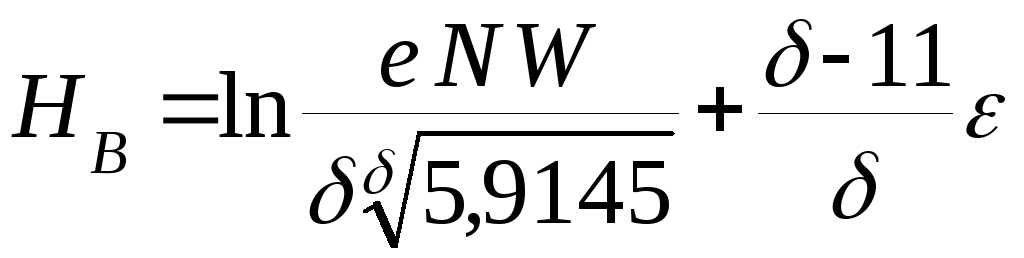, (5.19)

где – масштабный параметр распределения;

– параметр формы распределения;

– константа Эйлера.

в) Логарифмически-нормальное распределение:

, (5.20)

, (5.21)

где – параметры распределения.

Энтропию можно теперь представить следующим образом:

, (5.22)

откуда . Величина представляет независящую от числа групп часть энтропии – так называемую главную составляющую, называемую также дифференциальной энтропией.

Дифференциальная энтропия для приведенных выше распределений равна:

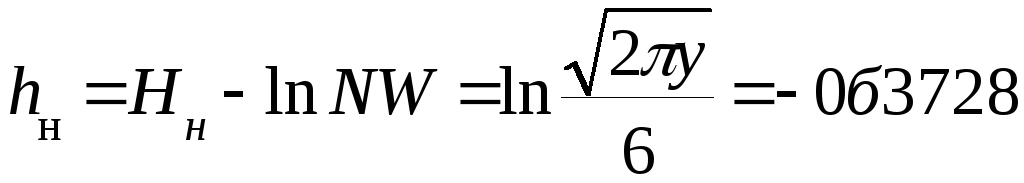, (5.23)

, (5.24)

. (5.25)

Для равномерного распределения:

. (5.26)

В табл. 5.4. представлена зависимость дифференциальной энтропии вейбулловского и логарифмически-нормального распределения от некоторых параметров распределения; указаны также частные случаи перехода к экспоненциальному и нормальному распределением.

Таблица 5.4. Дифференциальная энтропия вейбулловского и логарифмически-нормального распределений

Распределение Вейбулла			Логарифмически-нормальное распределение
		Частные случаи
0,5 1	2,4389 0,7774		0,1 0,5	1,1618 0,6652
2 3 3,754	0,2933 0,3063 0,3728		1 5	1,3631 10,8816
4 10	0,5032 0,9608		10	24,0985

С помощью дифференциальной энтропии можно теперь выбрать необходимое число дискретных значений рассматриваемого параметра , если – число всех внешних состояний, которые следует учесть при решении задачи.

Нетрудно показать, что справедливо следующее уравнение:

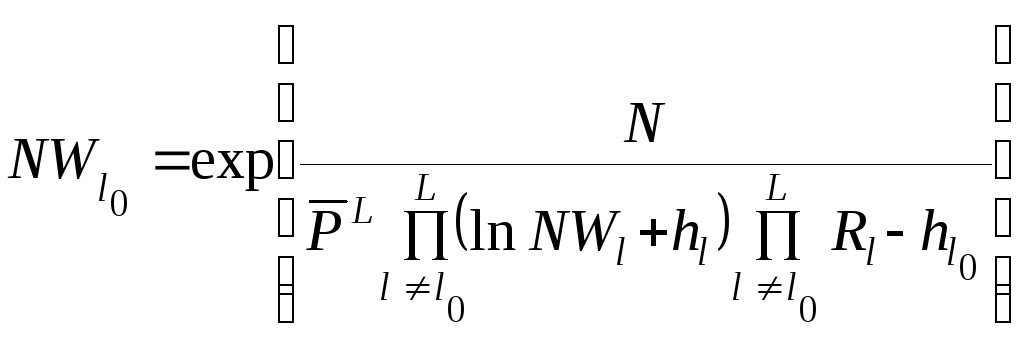, (5.27)

где – коэффициент пропорциональности;

– число рассматриваемых значений параметра;

– дифференциальная энтропия распределения параметра;

– релевантность параметра;

0 – индекс рассматриваемого параметра.

Это уравнение может быть использовано для определения числа групп итерационным способом, причем выбирается произвольно. Осуществляется это следующим образом:

,

и так далее, заканчивая, когда

,

где – допустимое отклонение.

Требования к точности приближения не должны устанавливаться слишком высокими, потому что все равно каждое число должно быть округлено. При практических расчетах число групп для одного параметра целесообразно задать заранее, причем в качестве базового параметра имеет смысл выбрать параметр с наиболее низкой релевантностью:

. (5.28)

Число групп для других параметров получают теперь из (5.7) и (5.22):

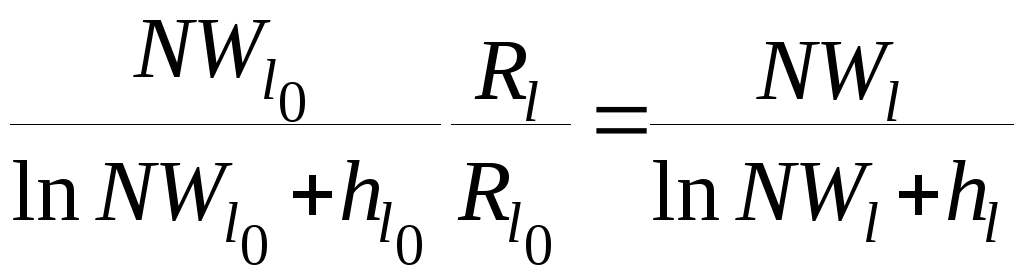(5.29)

с .

Из соображений возможности расчета обычно задается то максимальное число состояний исходных данных , которое можно обработать, так как справедливо отношение

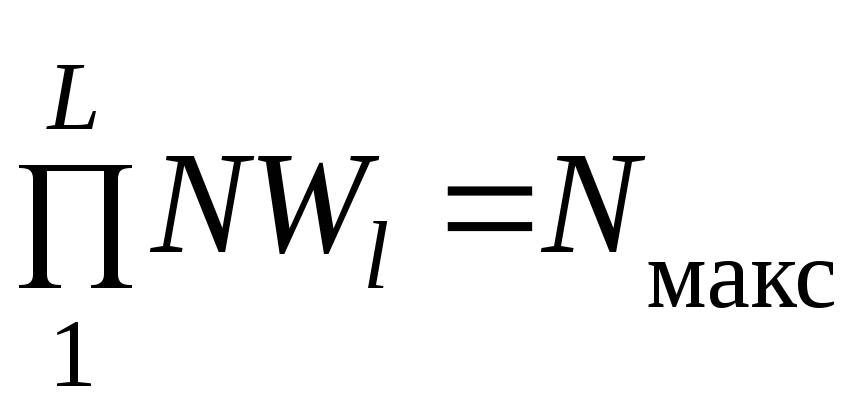. (5.30)

Варьируя шаг за шагом заданное вначале число групп достигают этой границы, причем целесообразно на основе соотношения

начинать с наименьшего числа

(5.31)

и увеличивать это число до тех пор, пока не будет достигнуто условие (5.30).

Однако и при этих условиях по формулам (5.29) – (5.30) не следует требовать излишней точности, так как, безусловно, будут необходимы округления результатов.