
- •Тема 1. Вступ. Дійсні числа
- •1. Вступ
- •2. Елементи теорії множин
- •Поняття відображення або функції.
- •1. Поняття відображення або функції
- •2. Потужність множин
- •3. Зчисленні множини
- •4. Математична індукція
- •1. Дійсні числа
- •1. Аксіоми додавання і множення
- •2. Аксіоми порівняння дійсних чисел
- •Аксіома неперервності дійсних чисел
- •2. Деякі властивості дійсних чисел
- •Із означення множини дійсних чисел випливає, що ця множина впорядкована.
- •1. Поняття ізоморфізму
- •2. Інтерпретація множини дійсних чисел
- •3. Найбільш вживані числові множини
- •4. Межі числових множин
- •5. Абсолютна величина числа
- •Абсолютна величина числа позначається символом .
- •Тема 2. Числові послідовності
- •1. Означення числової послідовності
- •2. Арифметичні дії над числовими послідовностями Нехай задано послідовності і .
- •2. Обмежені і необмежені числові послідовності
- •4. Нескінченно малі і нескінченно великі послідовності.
- •5. Основні властивості нескінченно малих послідовностей
- •1. Збіжні послідовності
- •2. Властивості збіжних послідовностей
- •3. Невизначені вирази.
- •1. Граничний перехід у нерівностях
- •2. Монотонні послідовності
- •3. Число е
- •4. Теорема про вкладені відрізки.
- •1. Теорема про вкладені відрізки.
- •3. Теорема Больцано-Вейєрштрасса
- •4. Критерій Коші збіжності числової послідовності.
- •1. Поняття метричного простору
- •2. Повні метричні простори.
- •3. Доповнення простору.
- •Тема 3. Границя функції однієї змінної
- •1. Границя функції. Означення границі функції за Гейне й за Коші.
- •2. Односторонні границі
- •3. Границя функції на нескінченності
- •4.Теореми про границі функцій
- •1. Визначні границі
- •2. Нескінченно малі й нескінченно великі функції
- •3. Порівняння нескінченно малих функцій. Еквівалентні нескінченно малі функції.
- •Тема 4. Неперервні та рівномірно неперервні функції
- •1. Неперервність функції в точці
- •2. Операції над неперервними функціями
- •1. Поняття рівномірної неперервності функції.
- •2. Теорема Кантора про рівномірну неперервність функції.
- •3. Теорема про неперервність оберненої функції.
- •Тема 5. Диференціальне числення функції однієї змінної
- •1. Задачі, що проводять до поняття похідної
- •Після спрощення одержуємо
- •2. Означення похідної
- •3. Механічний та геометричний зміст похідної
- •4. Односторонні похідні
- •5. Нескінченні похідні
- •1. Диференційовність функції
- •2. Похідні елементарних функцій
- •3. Похідна оберненої функції.
- •1. Диференціал функції
- •2. Похідні й диференціали вищих порядків
- •3. Формула Лейбніца для п-ної похідної добутку двох функцій.
- •4. Диференціали вищих порядків.
- •Тема 5. Застосування диференціального числення до дослідження функцій
- •1. Теореми про середнє значення
- •2. Теорема Ферма
- •3. Теорема Ролля
- •4. Теорема Лагранжа
- •5. Теорема Коші
- •1. Розкриття невизначеностей. Правило Лопіталя.
- •2. Застосування правила Лопіталя при розкритті невизначеностей вигляду .
- •1. Формула Тейлора для многочлена. Розглянемо многочлен
- •6.2. Формула Тейлора для довільної функції
- •Звідси одержуємо:
- •1. Ознака монотонності функції
- •3. Необхідні й достатні умови існування екстремуми функції
- •Достатні умови існування екстремуму функції.
- •1. Опуклість та вгнутість кривої. Точки перегину
- •2. Асимптоти графіка функції
- •3. Загальна схема дослідження функцій і побудови їх графіків
- •Тема 7. Інтеграл ньютоналейбніца
- •1. Поняття первісної функції та невизначеного інтеграла
- •2. Основні властивості невизначеного інтеграла
- •3. Таблиця основних інтегралів
- •5. Безпосереднє інтегрування
- •4. Метод підстановки
- •6. Інтегрування частинами
- •1. Подання раціональних дробів у вигляді суми найпростіших дробів
- •2. Інтегрування найпростіших раціональних дробів
- •1. Інтегрування ірраціональних функцій
- •Інтегрування деяких тригонометричних функцій
- •Приклади
6.2. Формула Тейлора для довільної функції
Теорема
Тейлора. Нехай функція
![]() в точці
в точці
![]() і в деякому її околі має похідні
і в деякому її околі має похідні
![]() -
го порядку. Нехай також
-
го порядку. Нехай також
![]() деяка точка, що належить околу, про який
йде мова. Тоді існує точка
деяка точка, що належить околу, про який
йде мова. Тоді існує точка
![]() ,
яка лежить між точками
,
яка лежить між точками
![]() і
і
![]() ,
така, що
,
така, що
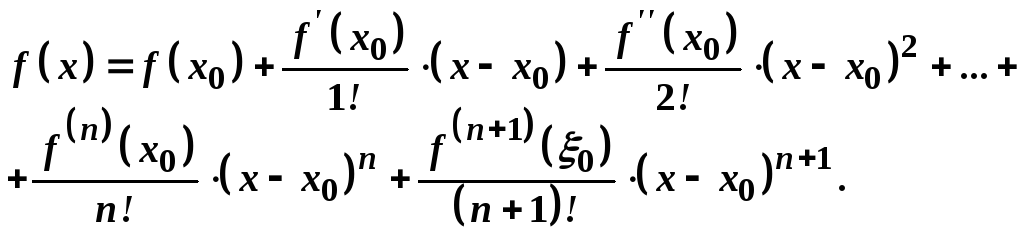 (3)
(3)
Доведення. Позначимо
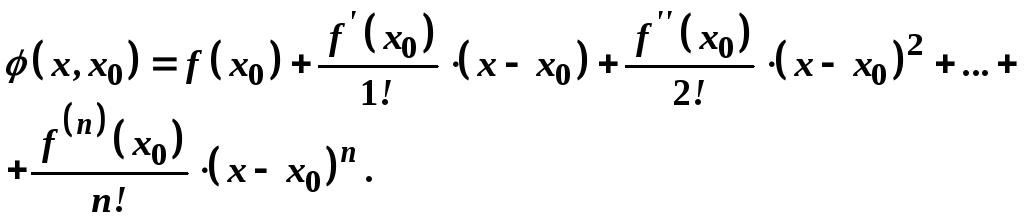
Покладемо
![]()
Покажемо, що існує точка
![]() така, що
така, що
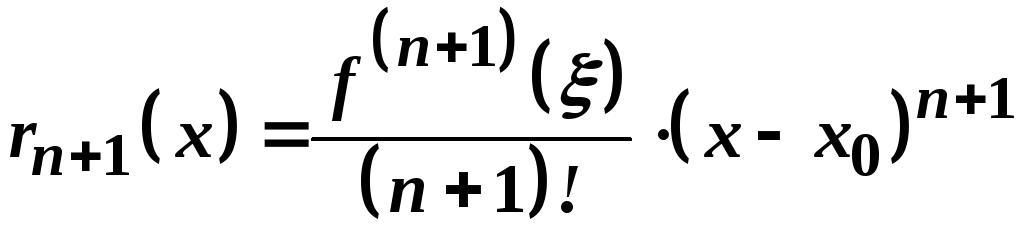 .
.
Зафіксуємо довільну точку
![]() із вказаного околу точки
із вказаного околу точки
![]() .
Для визначеності уважатимемо, що
.
Для визначеності уважатимемо, що
![]() .
Нехай
.
Нехай
![]()
змінна, яка пробігає значення відрізку
змінна, яка пробігає значення відрізку
![]() .
Складемо допоміжну функцію
.
Складемо допоміжну функцію
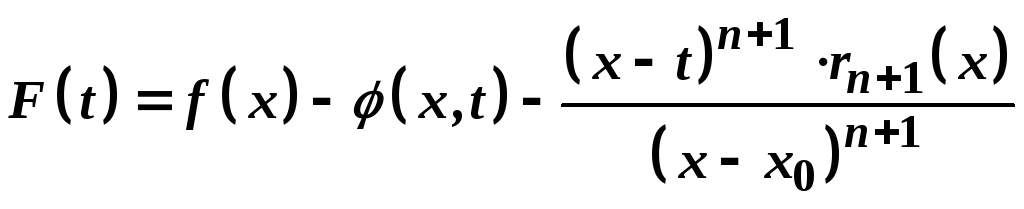 .
.
Функція
![]() на відрізку
на відрізку
![]() задовольняє всім умовам теореми Ролля:
задовольняє всім умовам теореми Ролля:
-
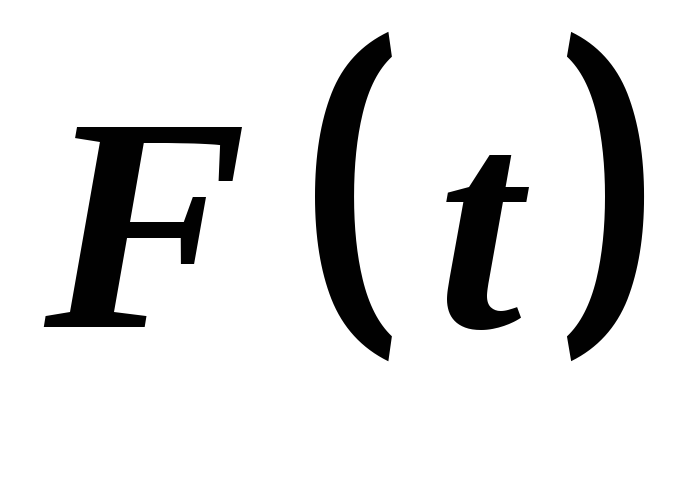 неперервна на
неперервна на
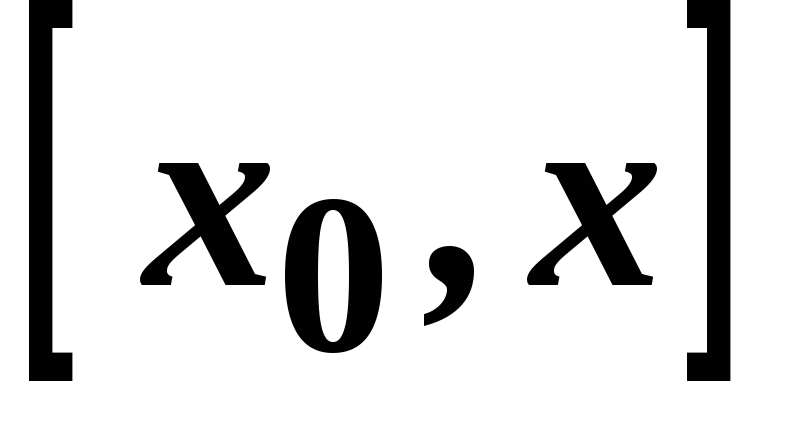 ,
, -
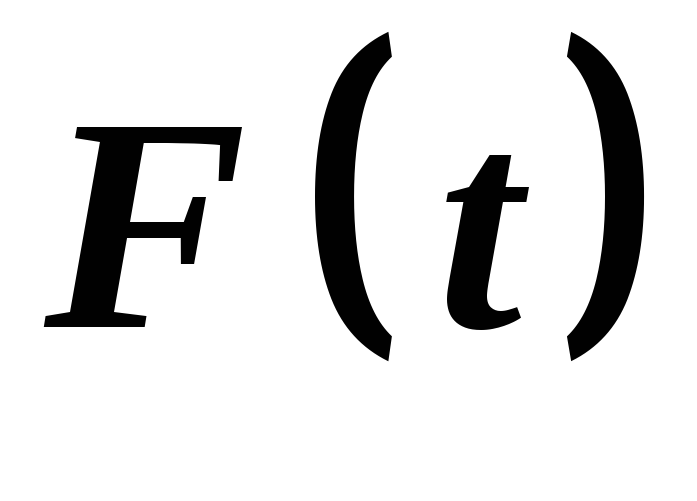 диференційована на
диференційована на
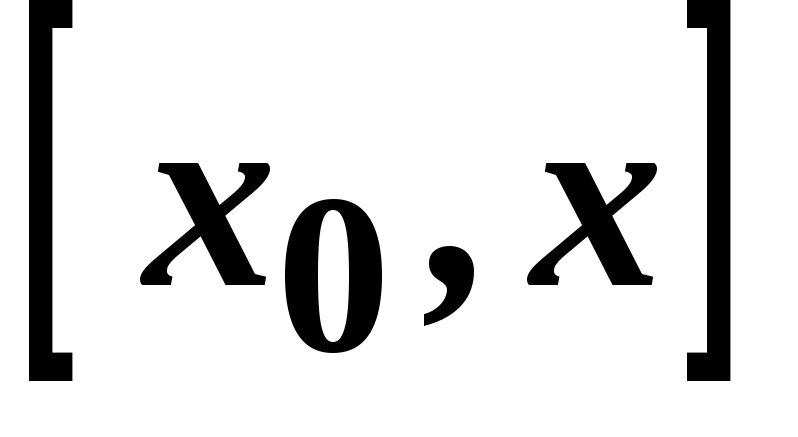 ,
,
(
ці властивості функції
![]() випливають із умов, накладених на функцію
випливають із умов, накладених на функцію
![]() )
)
-
на кінцях відрізка
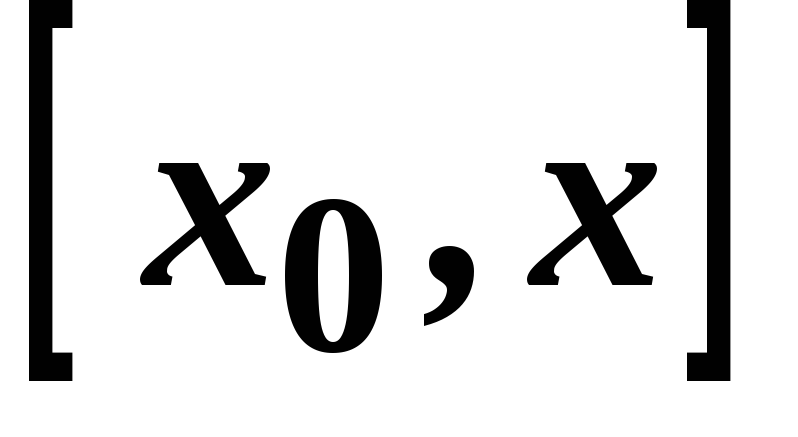 функція
функція
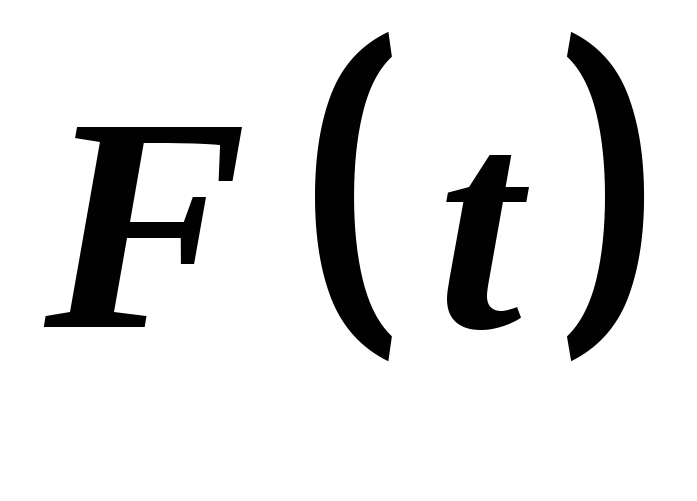 має рівні значення. Дійсно
має рівні значення. Дійсно
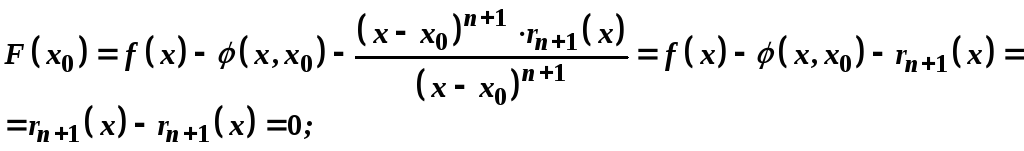

Отже,
за теоремою Ролля існує точка
![]() така, що
така, що
![]() .
Знайдемо
.
Знайдемо
![]() .
.
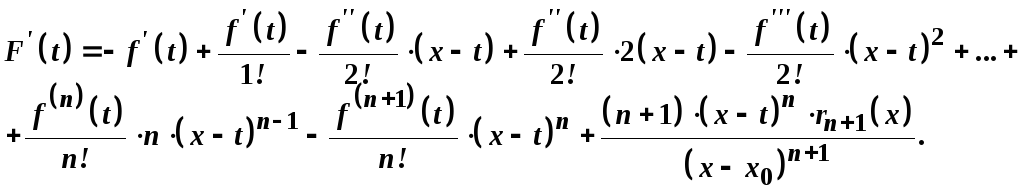
Оскільки в правій частині одержаної формули знищуються всі члени, за виключенням двох останніх, то
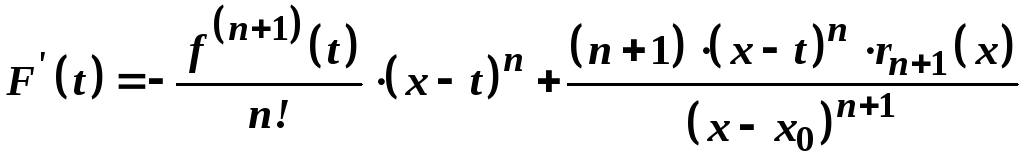 .
.
Далі маємо:
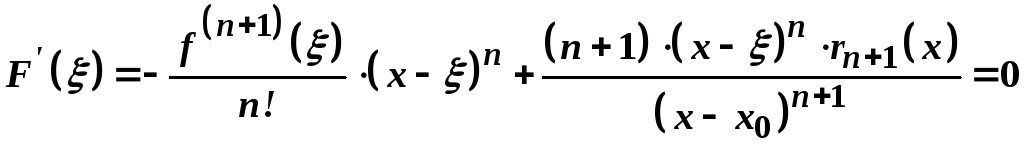 .
.
Звідси одержуємо:
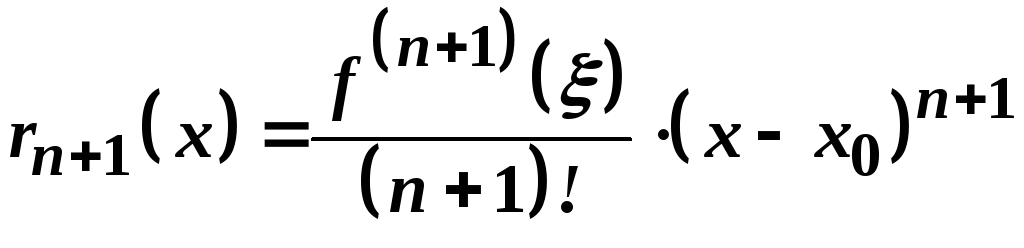 .
.
Формула (3) називається формулою Тейлора,
а одержаний вираз
![]() залишковим членом
у формі Лагранжа.
залишковим членом
у формі Лагранжа.
Оскільки
![]() ,
то
,
то
![]() ,
де
,
де
![]() .
Тоді
.
Тоді
 ,
де
,
де
![]() .
.
Якщо в формулі
Тейлора покласти
![]() ,
то тоді
,
то тоді

При
![]() маємо формулу Лагранжа
маємо формулу Лагранжа
![]()
Якщо функція
![]() в околі точки
в околі точки
![]() обмежена, то залишковий член
обмежена, то залишковий член
![]() є нескінченно малою вищого порядку
порівняно з
є нескінченно малою вищого порядку
порівняно з
![]() при
при
![]() .
Дійсно
.
Дійсно
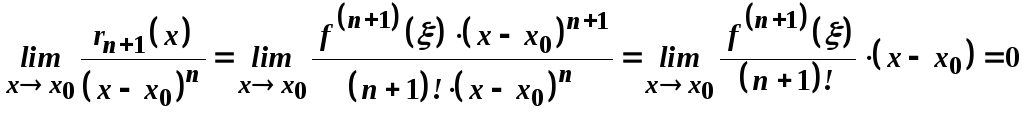 .
.
Отже, залишковий член
![]() можна подати у формі
можна подати у формі
![]() при
при
![]() ,
,
яка називається формою Пеано.
Якщо в формулі
Тейлора покласти
![]() ,
то одержимо формулу Маклорена
,
то одержимо формулу Маклорена
 .
.
У цій формулі залишковий член у формі Лагранжа має вигляд
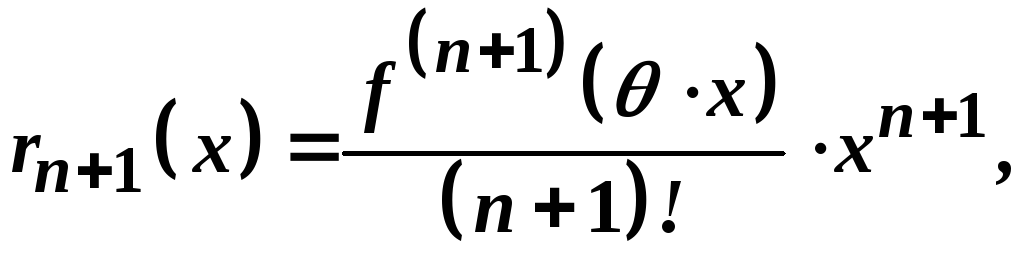 де
де
![]() ,
,
а в формі Пеано
![]() .
.
Приклади.
Записати формулу Маклорена для функції
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() .
.
Розв'язування.
-
 .
Оскільки
.
Оскільки
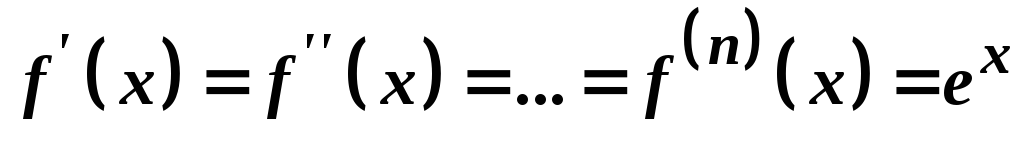 ,
то
,
то
 .
Отже,
.
Отже,
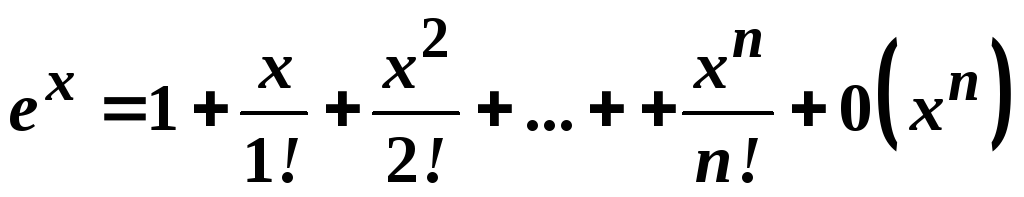 .
.
-
 .
Так як
.
Так як
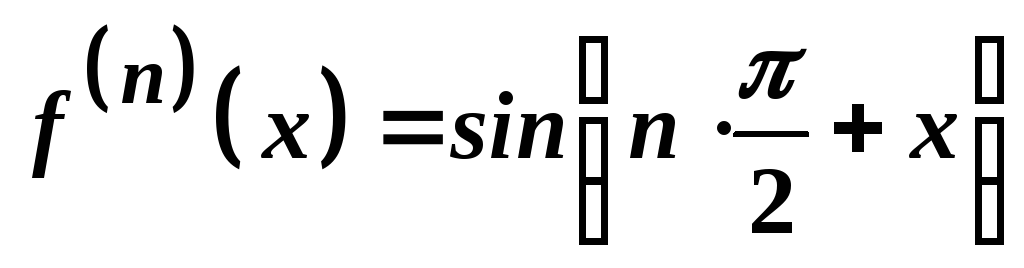 ,
то
,
то
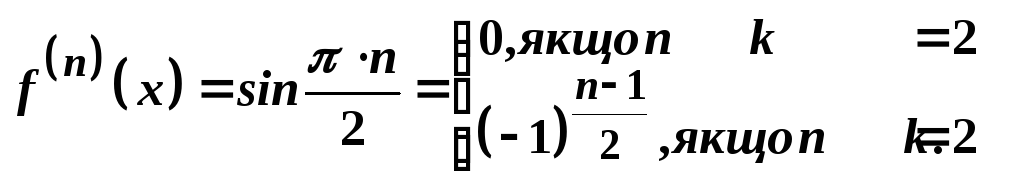
Звідси маємо
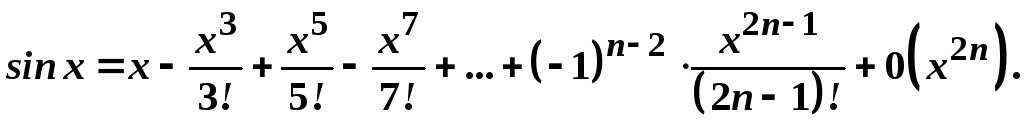
-
 .
.
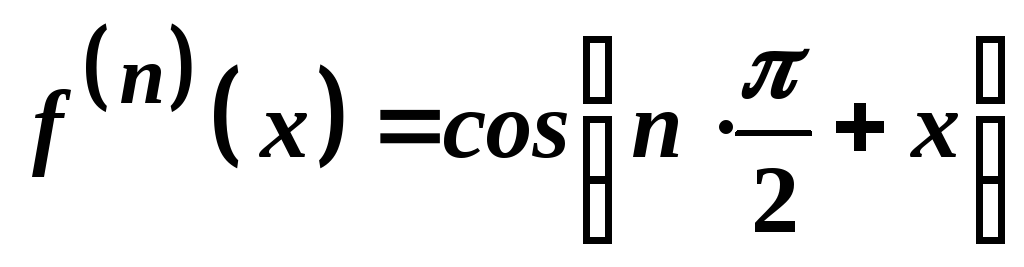 ;
;
 ;
;

ЛЕКЦІЯ 21
-
Ознака монотонності функції.
-
Екстремальні точки.
-
Необхідні й достатні умови існування екстремуми функції.
4. Знаходження найбільшого й найменшого значення функції на відрізку.
1. Ознака монотонності функції
Теорема . Якщо функція
![]() диференційована на інтервалі
диференційована на інтервалі
![]() і
і
![]() на
на
![]() ,
то функція
,
то функція
![]() зростає (спадає).
зростає (спадає).
Доведення. Нехай для визначеності
![]() .
Візьмемо в інтервалі
.
Візьмемо в інтервалі
![]() дві довільні точки
дві довільні точки
![]() такі, що
такі, що
![]() .
На відрізку
.
На відрізку
![]() функція
функція
![]() задовольняє умовам теореми Лагранжа.
Отже, існує точка
задовольняє умовам теореми Лагранжа.
Отже, існує точка
![]() така,
що
така,
що
 .
.
Звідси випливає, що за умов
![]() і
і
![]() маємо:
маємо:
![]() ,
тобто
,
тобто
![]() .
.
Для випадку
![]() доведення аналогічне.
доведення аналогічне.
2. Екстремальні точки
Точка
![]() називається точкою локального максимуму
(мінімуму) функції
називається точкою локального максимуму
(мінімуму) функції
![]() ,
якщо існує
,
якщо існує
![]() -
окіл
-
окіл
![]() точки
точки
![]() такий, що
такий, що
![]() для будь-якої відмінної від
для будь-якої відмінної від
![]() точки
точки
![]() .
При цьому саме значення
.
При цьому саме значення
![]() називається локальним максимумом
(мінімумом) функції
називається локальним максимумом
(мінімумом) функції
![]() .
.
Точки максимуму
і мінімуму функції
![]() називаються точками екстремуму або
екстремальними точками функції
називаються точками екстремуму або
екстремальними точками функції
![]() .
.
3. Необхідні й достатні умови існування екстремуми функції
Необхідна умова існування локального
екстремуму функції. Якщо в точці
![]() функція
функція
![]() має екстремум, то існує окіл
має екстремум, то існує окіл![]() точки
точки
![]() ,
в якому значення
,
в якому значення
![]() є найбільшим або найменшим. Отже, якщо
в точці
є найбільшим або найменшим. Отже, якщо
в точці
![]() функція
функція
![]() диференційована, то згідно теореми
Ферма
диференційована, то згідно теореми
Ферма
![]() .
.
Зазначимо,
що коли функція
![]() диференційована в точці
диференційована в точці
![]() і
і
![]() ,
то або
,
то або
![]() ,
тобто функція зростає, або
,
тобто функція зростає, або
![]() і функція спадає. Звідси випливає, що
функція
і функція спадає. Звідси випливає, що
функція
![]() може мати екстремум лише в тих точках,
у яких її похідна
може мати екстремум лише в тих точках,
у яких її похідна
![]() рівна нулю, або не існує.
рівна нулю, або не існує.
Точки, в яких
похідна функції
![]() рівна нулю, називаються стаціонарними.
Стаціонарні точки й точки, в яких функція
рівна нулю, називаються стаціонарними.
Стаціонарні точки й точки, в яких функція
![]() визначена, але її похідна
визначена, але її похідна
![]() не існує називаються критичними.
не існує називаються критичними.
Отже, для
того, щоб функція
![]() мала в точці
мала в точці
![]() екстремуму, необхідно, щоб ця точка була
критичною.
екстремуму, необхідно, щоб ця точка була
критичною.
