Доказательство.

Проведём доказательство методом математической индукции, взяв в качестве параметра индукции число элементов во множестве .

1-й шаг (случай |x|=1). Применяя лемму 1, имеем:

.

2-й шаг (индуктивный переход). Допустим, что теоремы справедливы для любого -элементного множества. Докажем, что в этом случае оно справедливо и для множества такого, что . Зафиксируем в произвольный элемент и применим лемму 2.

.

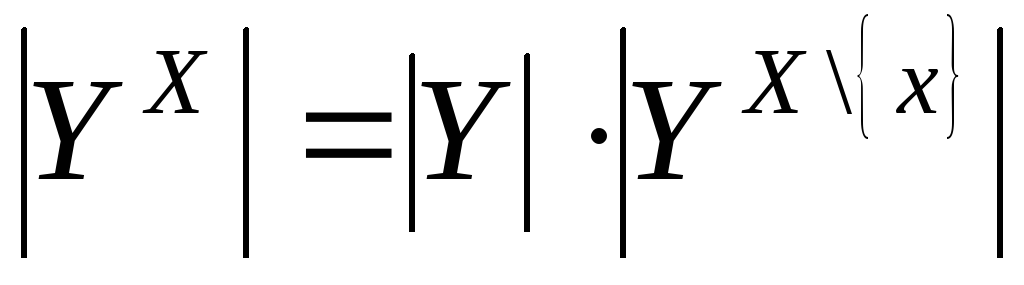Множество содержит элементов и к применимо предложение индукции, тогда

.

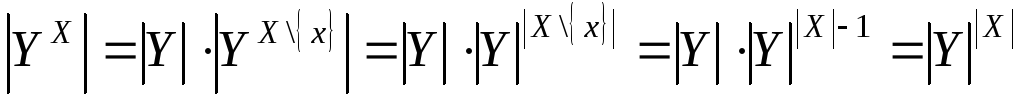Индуктивный переход, а значит, и вся теорема доказаны.

4. Примеры задач и упражнений.

8. Основная часть: практическая работа студентов

Практическое занятие №1. Разработка синтаксических анализаторов для регулярных языков.

1. Общие указания к выполнению практической работы.

Практические работы выполняются с использованием персональных компьютеров. Указания по технике безопасности совпадают с требованиями, предъявляемыми к пользователю ЭВМ. Другие опасные факторы отсутствуют.

2. Цель работы

Написание, отладка и проверка работоспособности синтаксического анализатора на основе графа детерминированного конечного автомата, соответствующего заданному регулярному выражению, порождающему конкретный язык.

3. Постановка задачи

7.03.1. Описание грамматики.

Рассмотрим регулярное выражение (221b)* (b21)* (22)*. Это выражение порождает предложения языка:

L = {(221b)^m (b21)ⁿ (22)^p: m, n, p > 0}.

Языку L соответствует регулярная порождающая грамматика: G = ({1, 2, b}, (А, В, С, D, Е, F, К, L, M, S}, P, S), где Р={S→2A; А→2В; В→1C; С→bS; S→ε; S→2D; D→2Е; Е→IF; F→bD; F→ε; F→2K; K→2L; L→2M; M→2L; L→ε; В→ε; В→2K} — порождающие правила; {1, 2, b} — множество терминальных символов; {А, В, С, D, Е, F, К, L, M, S} — множество нетерминальных символов; S — аксиома; ε — пустая строка.

Для каждой регулярной грамматики существует детерминированный конечный автомат. Грамматике G соответствует автомат:

M = ({А, В, С, S, D, Е, F, К, L, М), {1, 2, b}, d, {S}, (S, В, F, L}), где {А, В, С, S, D, Е, F, К, L, М} — конечное множество состояний; {1, 2, Ь} — конечный входной алфавит; d — множество переходов:

{d(S, 2) = A; d(S, b) = D; d(F, 2) = K;

d(A,2) = B; d(D,2) = E; d(B,2) = K;

d(B, 1) = C; d(E,l) = F; d(K,2) = L;

d(C, b) = S; d(F, b) = D; d(L, 2) = M;

d(M,2) = L};

S - начальное состояние (S {A, B, C, S, D, E, F, K, L, M});

{S, B, F, L} - множество последних состояний

({S, В, F, L} {A, B, C, S, D, E, F, K, L, M}).

Множество переходов d может быть эквивалентно представлено таблицей переходов:

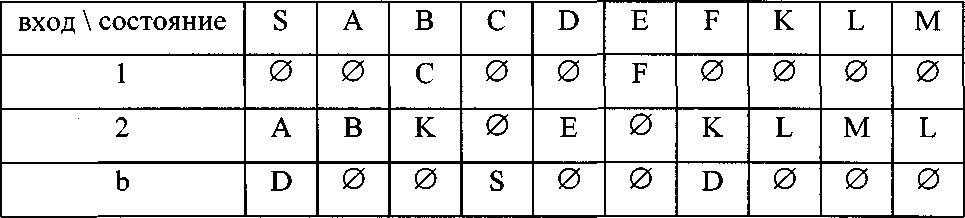
Здесь  — пустое множество.

Здесь состояния S, В, F, L являются последними.

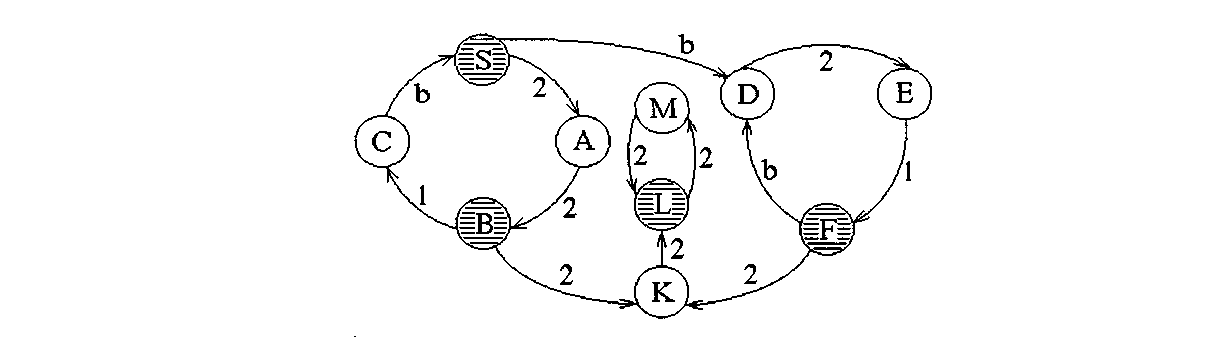
Множество переходов также может быть представлено графически с помощью графа переходов из одного состояния детерминированного конечного автомата в другое. Для рассматриваемого варианта граф имеет следующий вид:

8.2. Формулировка задания.

Для заданного варианта регулярного выражения написать регулярную грамматику.

Представить детерминированный конечный автомат, соответствующий регулярной грамматике.

Написать и проверить работоспособность соответствующего синтаксического анализатора.

Краткие сведения из теории

Конечный автомат — это устройство для распознавания строк какого-либо языка. Конечный автомат — это пятерка М = (К, , , S, F),

где K — конечное множество состояний;

 — конечный входной алфавит;

 — множество переходов;

S — начальное состояние (S  К);

F — множество последних состояний (F  К).

По мере считывания каждой литеры строки автоматом контроль передается от состояния к состоянию в соответствии с заданным множеством переходов.