– 51(x + 4) – 41(y – 1) – 42(z – 7) = 0;
– 51x – 41y – 42z + 131 = 0.
Это и есть уравнение (3) .
е)
В качестве вектора нормали к искомой
плоскости (4)
можно взять векторное произведение
на
–
нормалей к плоскости (’)
и (”):
.
Зная
точку M(–4;1;7)
, через которую проходит плоскость (4),
и вектор нормали
,
составляем уравнение (4):
17(x + 4) + 1 (y – 1) + 14 (z – 7) = 0;
17x + y + 14z – 31 = 0.
ж) Запишем ещё раз уравнения (L) в параметрической форме:
, (1)
Подставим эти выражения в уравнение плоскости ():
–2(4t + 5) + (–6t – 2) + 3(t – 1) – 1 = 0;
–11t
= 16;
.
Подставив найденное t в (1), находим координаты искомой точки:
, 
Таким
образом, точкой пересечения (L)
и ()
является
.
з)
.
Пример 8. Составить канонические уравнения прямой (L), заданной в виде
(2)
Решение. Прямая (L) задана как пересечение плоскостей
(1):–3x
+ 2y
– z
+ 1 = 0 и (2):
x
– 5y
+ 6z
+ 21 = 0. Векторы нормалей
,
перпендикулярны к (L).
Поэтому в качестве направляющего вектора
q
прямой (L)
можно взять векторное произведение
:
=
.
Для
составления канонических уравнений
прямой достаточно знать её направляющий
вектор и точку, через которую проходит
прямая. Найдём некоторую точку (L).
Определитель
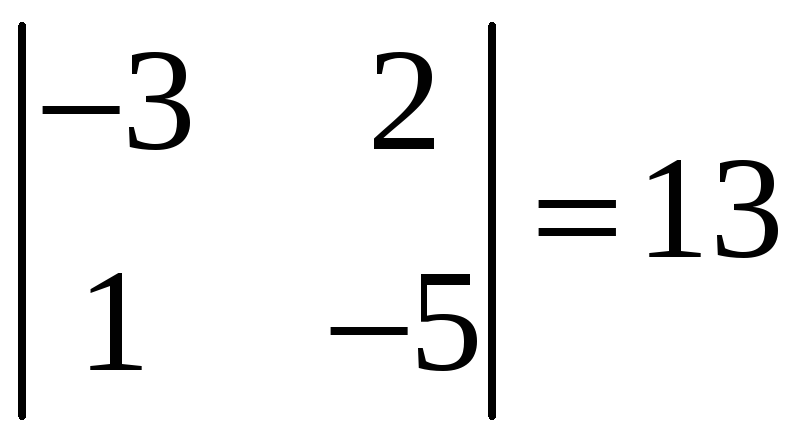отличен от нуля. Перепишем систему (2) в
виде
Положим
(можно было взять любое другое), получим
систему
Эта система имеет решение x = 47/13, y = 64/13. Вспомнив, что z = 0, находим точку прямой (L): M(47/13; 64/13; 0). Составим уравнение прямой (L) по её направляющему вектору q {7; 17; 13} и точке M(47/13; 64/13; 0), через которую она проходит:
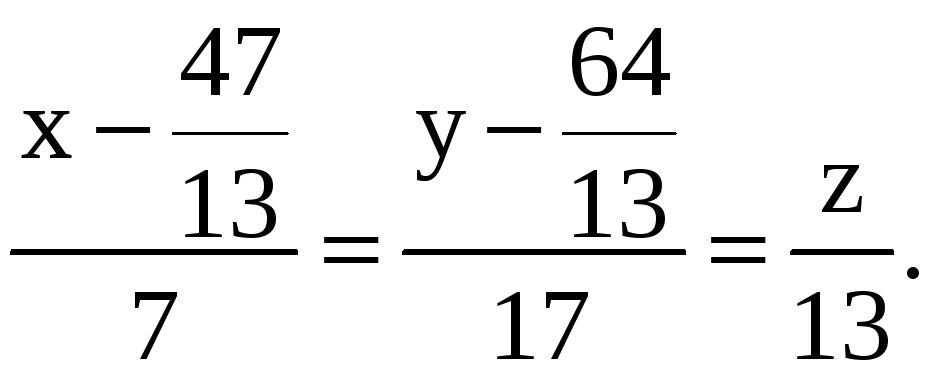
5. Кривые второго порядка на плоскости
Эллипсом называется геометрическое место всех таких точек на плоскости, для которых сумма расстояний до двух фиксированных точек плоскости F1 и F2, называемых фокусами, есть величина постоянная.
Гиперболой называется геометрическое место всех таких точек на плоскости, для которых разность расстояний до двух фиксированных точек плоскости F1 и F2, называемых фокусами, есть величина постоянная.
Параболой называется геометрическое место всех таких точек на плоскости, для каждой из которых расстояние до некоторой фиксированной точки F, называемой фокусом, равно расстоянию до некоторой фиксированной прямой, называемой директрисой.
Для каждой из этих кривых существует такая декартова прямоугольная система координат, что кривая описывается каноническим уравнением
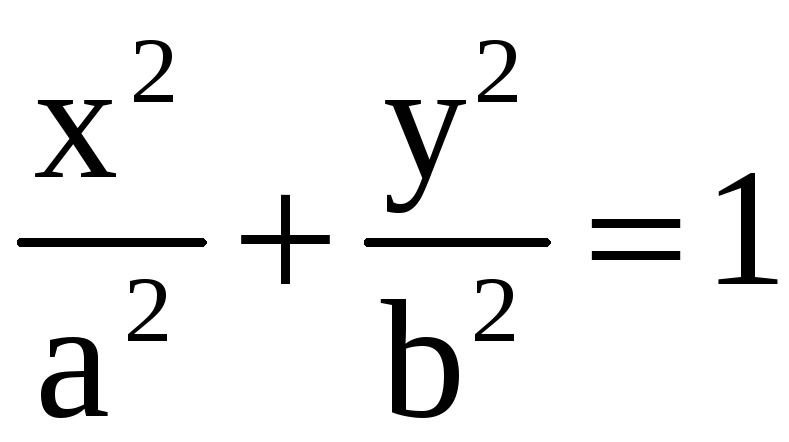
для эллипса,
для гиперболы,
для параболы.
Э
ллипс,
заданный уравнением в канонической
форме, имеет центр симметрии – точку
0, две оси симметрии – координатные оси
0x и 0y, заключён в прямоугольнике –a
x
a, –b
y
b и касается его сторон.
Гипербола, заданная
уравнением в канонической форме, имеет
центр симметрии – точку 0, две оси
симметрии – координатные оси 0x и 0y,
имеет две асимптоты – прямые
и
.
Парабола, заданная уравнением в канонической форме, имеет одну ось симметрии – ось 0x .
Алгебраической кривой второго порядка называется кривая, которая в декартовой прямоугольной системе координат задаётся уравнением
. (3)
Если кривая, задаваемая уравнением (3), не является вырожденной, то она является либо эллипсом, либо гиперболой, либо параболой (к вырожденным относятся: пустое множество, точка, пара точек, прямая, пара прямых).
Пример 9.
Дано уравнение кривой в полярной системе
координат:
:
а) изобразить кривую по точкам, придавая
значения из промежутка
с шагом /8;
б) составить уравнение этой кривой в декартовой прямоугольной системе координат, согласованной с полярной, и определить вид этой кривой.
Решение. а) Составим таблицу значений функции.
|
|
0 |
/8 |
/4 |
3/8 |
/2 |
5/8 |
3/4 |
7/8 |
|
|
3 |
2,8 |
2,32 |
1,72 |
1,5 |
1,26 |
1,11 |
1,02 |
|
|
|
9/8 |
5/8 |
11/8 |
3/2 |
13/8 |
7/4 |
15/8 |
|
|
1 |
1,02 |
1,11 |
1,26 |
1,5 |
1,72 |
2,32 |
2,8 |
По этим данным отметим точки на плоскости и, плавно соединяя соседние точки, построим линию.
б) Перейдём к
декартовой прямоугольной системе
координат, пользуясь формулами
,
,
:
;
;
;
;
4(x2 + y2) = x2 + 6x + 9; 3x2 – 6x + 4y2 = 9;
3(x2
– 2x + 1 – 1) + 4y2
= 9; 3(x – 1)2
+4y2
= 12;
.
Это уравнение эллипса с центром в точке (1; 0) и полуосями
a = 2,
.
Задание 4.1
Докажите,
что векторы
образуют базис. Найдите разложение
вектора a
в этом базисе.
|
№ |
|
|
|
|
|
1 |
{3;–2;1} |
{1;1;–4} |
{–2;3;1} |
{–1;–1;3} |
|
2 |
{2;1;–1} |
{–3;–2;1} |
{4;2;–3} |
{–2;–2;4} |
|
3 |
{–1;–2;3} |
{2;0;–4} |
{3;–2;1} |
{5;–1;–2} |
|
4 |
{–4;–1;1} |
{3;–2;–1} |
{2;–5;3} |
{–2;1;0} |
|
5 |
{–3;1;–2} |
{4;–2;–1} |
{1;–1;2} |
{3;1;–4} |
|
6 |
{2;–1;2} |
{3;1;–4} |
{4;3;–1} |
{0;2;–3} |
|
7 |
{1;–3;2} |
{2;0;–1} |
{0;6;1} |
{–5;2;–1} |
|
8 |
{–2;–2;1} |
{3;1;–2} |
{1;–1;3} |
{4;–2;1} |
|
9 |
{1;–2;4} |
{–2;–3;1} |
{1;5;–2} |
{3;0;2} |
|
10 |
{4;1;–1} |
{–3;1;–1} |
{1;3;–4} |
{–2;1;–1} |
|
11 |
{–2;0;5} |
{3;–1;2} |
{1;–1;1} |
{2;–4;3} |
|
12 |
{–5;1;–1} |
{–2;–2;3} |
{–1;5;1} |
{0;–1;2} |
|
13 |
{2;–4;5} |
{3;1;–3} |
{–1;–5;0} |
{2;3;–5} |
|
14 |
{–4;–2;1} |
{0;2;–1} |
{3;–2;–2} |
{5;–1;1} |
|
15 |
{–3;–3;2} |
{2;–1;4} |
{–1;–4;1} |
{2;–3;–2} |
|
16 |
{–1;5;1} |
{3;–2;0} |
{2;3;3} |
{–4;–1;1} |
|
17 |
{2;–3;–2} |
{–1;–1;4} |
{–1;–6;1} |
{–2;–3;1} |
|
18 |
{–1;–1;5} |
{2;–1;–3} |
{1;–2;–1} |
{3;–1;1} |
|
19 |
{0;2;–1} |
{3;–1;–3} |
{3;1;–2} |
{1;–4;–1} |
|
20 |
{–5;1;–1} |
{2;1;–3} |
{–3;2;1} |
{4;2;–3} |
|
21 |
{2;–3;2} |
{1;–4;–1} |
{1;3;–2} |
{1;0;–5} |
|
22 |
{4;–1;5} |
{–2;3;1} |
{2;2;–1} |
{3;1;–1} |
|
23 |
{–2;1;5} |
{3;–3;1} |
{1;–2;2} |
{3;1;0} |
|
№ |
|
|
|
|
|
24 |
{–1;1;6} |
{2;–3;–1} |
{1;2;–1} |
{–4;–1;–2} |
|
25 |
{3;–1;5} |
{2;–2;–1} |
{4;0;–1} |
{–3;–2;1} |
|
26 |
{2;2;–5} |
{–1;2;–1} |
{3;6;–1} |
{2;–4;1} |
|
27 |
{–3;–1;2} |
{2;–4;0} |
{4;–1;1} |
{–5;1;–1} |
|
28 |
{1;–5;2} |
{–2;1;1} |
{3;–6;–3} |
{1;–1;7} |
|
29 |
{–4;1;4} |
{2;–1;3} |
{0;–1;2} |
{1;–3;4} |
|
30 |
{2;–5;2} |
{–1;3;0} |
{1;–2;3} |
{4;–4;3} |
