
- •Глава 7. Дифференциальные уравнения
- •7.1. Общие понятия
- •7.2. Дифференциальные уравнения первого порядка
- •7.3. Задача Коши. Теорема о существовании и единственности решения дифференциального уравнения первого порядка
- •7.4. Дифференциальные уравнения с разделяющимися переменными
- •7. 5. Однородные дифференциальные уравнения (дифференциальные уравнения с однородными функциями)
- •7.6. Линейные дифференциальные уравнения первого порядка
- •7.7. Уравнение Бернулли
- •7.8. Дифференциальные уравнения первого порядка в полных дифференциалах
- •7.9. Дифференциальные уравнения высших порядков
- •7. 10. Дифференциальное уравнение вида
- •7.11. Дифференциальные уравнения второго порядка, приводимые к дифференциальным уравнениям первого порядка
- •7.12. Линейные дифференциальные уравнения n-ого порядка. Свойства их решений
- •7.13. Линейная зависимость функций. Определитель Вронского
- •7.14. Структура общего решения линейного неоднородного дифференциального уравнения n-ого порядка
- •7.15. Комплексные числа и действия над ними
- •Действия над комплексными числами
- •7.16. Показательная функция с комплексным показателем
- •7.17. Показательная форма комплексного числа. Формула Эйлера
- •7.18. Общее решение линейного однородного дифференциального уравнения n-ого порядка с постоянными коэффициентами.
- •7.19. Частное решение линейного неоднородного дифференциального уравнения n-ого порядка с постоянными коэффициентами
- •7.20. Метод Эйлера численного интегрирования дифференциальных уравнений
7.19. Частное решение линейного неоднородного дифференциального уравнения n-ого порядка с постоянными коэффициентами
Вид частного решения неоднородного дифференциального уравнения
![]()
зависит от вида
правой части этого уравнения (функции
![]() )
и от величин корней характеристического
уравнения.
)
и от величин корней характеристического
уравнения.
Рассмотрим
нахождение частного решения для двух
видов функции
![]() .
.
Случай 1. Правая часть уравнения
![]() ,
,
где
вещественное значение,
![]()
многочлен m-й
степени.
многочлен m-й
степени.
В этом случае частное решение уравнения ищется в виде
![]()
где
![]()
многочлен m-й
степени,
многочлен m-й
степени,
s
степень кратности корня характеристического
уравнения
![]() .
.
Если
![]() не является корнем характеристического
уравнения, то s
= 0.
не является корнем характеристического
уравнения, то s
= 0.
Пример 7. 25.
Решить уравнение
![]() .
.
Характеристическое
уравнение однородного уравнения
![]() имеет один корень
имеет один корень
![]() кратности 2. Поэтому общее решение
однородного уравнения имеет вид
кратности 2. Поэтому общее решение
однородного уравнения имеет вид
![]() .
.
Находим частное
решение неоднородного уравнения. Правая
часть уравнения
![]() ,
т. е.
,
т. е.
![]() .
Данное значение
.
Данное значение
![]() не является корнем характеристического
уравнения (следовательно, его кратность
s
= 0). В этом случае частное решение ищется
в виде
не является корнем характеристического
уравнения (следовательно, его кратность
s
= 0). В этом случае частное решение ищется
в виде
![]() .
Находим производные
.
Находим производные
![]() и подставляем их в исходное уравнение
и подставляем их в исходное уравнение
![]() .
.
Делим это уравнение
на
![]() ,
имеем
,
имеем
![]() .
Отсюда
.
Отсюда
![]() .
.
Записываем частное
решение
![]() и общее решение
и общее решение
![]() .
.
Пример 7. 26.
Решить уравнение
![]() .
.
Общее решение
неоднородного уравнения равняется
сумме общего решения соответствующего
однородного уравнения и частного решения
неоднородного уравнения
![]() .
.
Найдем общее
решение однородного уравнения
![]() .
Его характеристическое уравнение
.
Его характеристическое уравнение
![]() имеет корни
имеет корни
![]() .
Общее решение
.
Общее решение
![]() .
.
Найдем частное решение неоднородного уравнения. Правую часть этого уравнения можно представить в виде
![]() ,
,
где показатель
степени
в функции
![]() равен
= 0. Это значение совпадает с корнем
характеристического уравнения
равен
= 0. Это значение совпадает с корнем
характеристического уравнения
![]() ,
т. е. является его корнем кратности s
= 1. Поэтому частное решение нужно искать
в виде
,
т. е. является его корнем кратности s
= 1. Поэтому частное решение нужно искать
в виде
![]() .
.
Находим производные
этой функции
![]() и подставляем их в исходное уравнение.
Получаем
и подставляем их в исходное уравнение.
Получаем
![]()
![]() .
.
Приравниваем
коэффициенты при одинаковых степенях
х
(![]() и
и
![]() )
в левой и правой частях уравнения
)
в левой и правой частях уравнения
![]()
Получаем систему для нахождения коэффициентов A и B
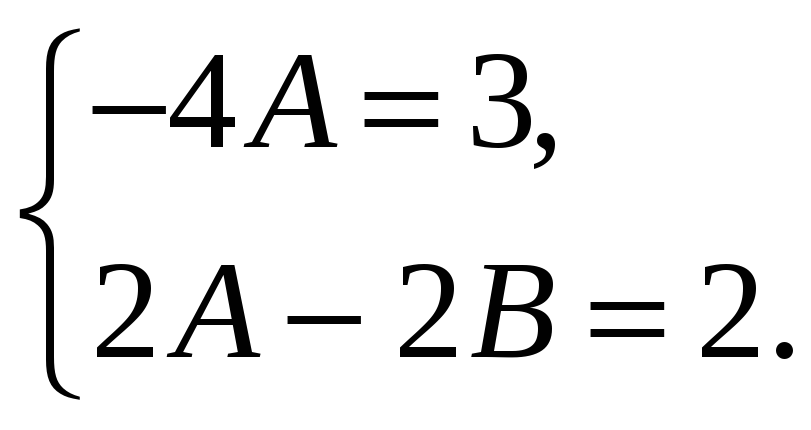
Отсюда
![]() ,
,
![]() .
Записываем частное решение
.
Записываем частное решение
![]() .
.
Общее решение исходного дифференциального уравнения
![]() .
.
Случай 2. Правая часть неоднородного дифференциального уравнения имеет вид
![]() ,
,
где и вещественные значения,
![]() и
и
![]()
многочлены степени
многочлены степени
![]() и
и
![]() соответственно.
соответственно.
В этом случае частное решение дифференциального уравнения ищется в виде
![]() ,
,
![]() многочлены
степени
многочлены
степени
![]() ,
,
s
кратность корня характеристического
уравнения
![]() ,
где
,
где
![]() совпадает с числом
в показателе степени
совпадает с числом
в показателе степени
![]() в функции
в функции
![]() правой части уравнения. Если
в
правой части уравнения. Если
в
![]() не совпадает с
не совпадает с
![]() ,
то s
= 0.
,
то s
= 0.
Пример 7. 27.
Решить уравнение
![]() .
.
Характеристическое
уравнение
![]() имеет комплексно-сопряженные корни
имеет комплексно-сопряженные корни
![]() .
Поэтому общее решение однородного
уравнения
.
Поэтому общее решение однородного
уравнения
![]() имеет вид
имеет вид
![]() .
.
Ищем частное
решение неоднородного уравнения. Правая
часть уравнения
![]() ,
т. е.
= 0. Значение
= 0 не совпадает с реальной частью корней
характеристического уравнения
,
т. е.
= 0. Значение
= 0 не совпадает с реальной частью корней
характеристического уравнения
![]() ,
поэтому s
= 0. Частное решение необходимо искать
в виде
,
поэтому s
= 0. Частное решение необходимо искать
в виде
![]() ,
,
где А и В постоянные величины.
Находим производные
![]() ,
подставляем их в исходное неоднородное
уравнение
,
подставляем их в исходное неоднородное
уравнение
![]()
![]() .
.
Приравниваем коэффициенты при sinx и cosx в левой и правой частях этого уравнения. Получаем систему для нахождения постоянных А и В и решаем ее.
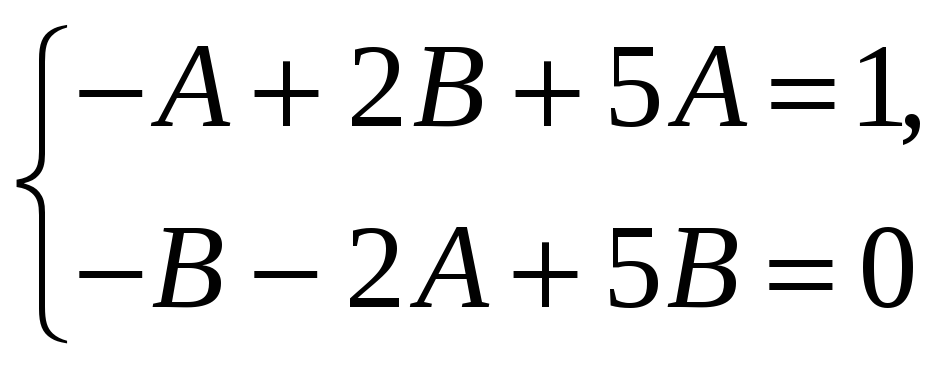

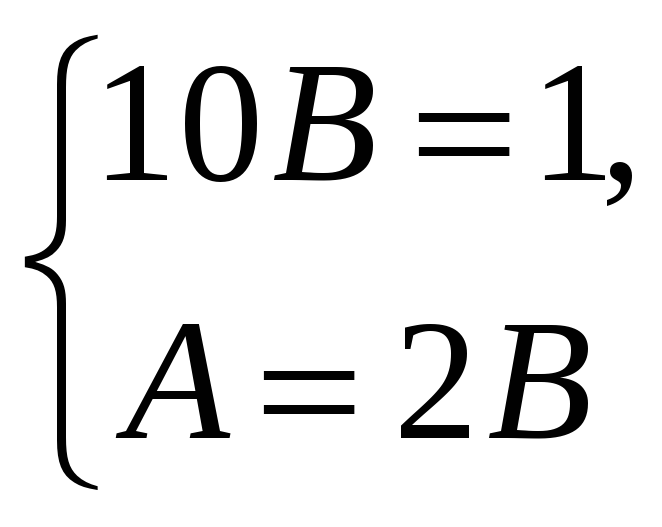
![]() ,
,
![]() .
.
Записываем частное решение
![]()
и общее решение
![]() .
.
