
- •Глава 5. Определенный интеграл
- •5.1. Задачи, приводящие к понятию определенного интеграла
- •5.2. Интегральные суммы, их свойства
- •Определение определенного интеграла
- •5.3. Взаимосвязь определенного и неопределенного интегралов. Формула Ньютона - Лейбница
- •5.4. Свойства определенного интеграла
- •5.5. Методы интегрирования определенных интегралов
- •5.6. Несобственные интегралы с бесконечными пределами интегрирования
- •5.7. Теоремы о сходимости несобственных интегралов с бесконечными пределами интегрирования
- •5.8. Несобственные интегралы от разрывных функций, неограниченных в точках разрыва
- •5.9. Теоремы о сходимости несобственных интегралов от разрывных функций
- •5.10. Геометрические приложения определенных интегралов
- •5.10.1. Вычисление площадей фигур
- •5.10.2. Вычисление объемов тел вращения
- •5.10.3. Длина дуги кривой
- •5.11. Численные методы нахождения определенных интегралов
- •5.11.1. Формулы прямоугольников
- •5.11.2. Формула трапеций
- •5.11.3. Формула Симпсона для приближенного вычисления определенных интегралов
- •5.12. Производная интеграла, зависящего от параметра
- •Глава 6. Двойные интегралы
- •6.1. Определение двойного интеграла
- •6.2. Геометрический смысл двойного интеграла
- •6.3. Свойства двойных интегралов
- •6.4. Вычисление двойных интегралов
- •6.5. Двойные несобственные интегралы с бесконечными пределами интегрирования
Определение определенного интеграла
Определенным
интегралом функции
![]() непрерывной на отрезке
непрерывной на отрезке
![]() называется предел интегральной суммы
при стремлении числа элементарных
отрезков к бесконечности, а длины
наибольшего из них к нулю, т.е.
называется предел интегральной суммы
при стремлении числа элементарных
отрезков к бесконечности, а длины
наибольшего из них к нулю, т.е.
 .
.
5.3. Взаимосвязь определенного и неопределенного интегралов. Формула Ньютона - Лейбница
Неопределенный
интеграл равен
![]() ,
где С
= const,
,
где С
= const,
F(x) – первообразная функция.
|
Рис. 59 |
Ранее было показано, что одной из первообразных функций является площадь криволинейной трапеции с переменной правой граничной прямой. По геометрическому смыслу определенный интеграл также равняется площади криволинейной трапеции, т. е.
|
При
![]() .
Тогда
.
Тогда
 .
Отсюда
.
Отсюда
 .
.
Эта формула называется формулой Ньютона-Лейбница.
5.4. Свойства определенного интеграла
Свойство 1. Постоянный множитель можно выносить из-под знака определенного интеграла, т. е.
 .
.
Д о к а з а т е л ь с т в о. Используем определение определенного интеграла и свойства пределов
 .
.
Свойство 2. Интеграл суммы функций равен сумме интегралов этих функций, т. е.
 .
.
Д о к а з а т е л ь с т в о. Так же используем определение определенного интеграла и свойства пределов
 =
=
 .
.
Свойство 3. При перестановке пределов интегрирования интеграл изменяет знак, т. е.
 .
.
Для доказательства используем формулу Ньютона-Лейбница.
 .
.
Свойство 4. Любой определенный интеграл можно разбить на сумму двух интегралов, если подынтегральная функция непрерывна в пределах интегрирования, т. е.
 .
.
Д о к а з а т е л ь с т в о.
 .
.
Свойство 5. Если
для любого х
на отрезке
![]()
![]() ,
то
,
то
 .
.
Д о к а з а т е л ь
с т в о. По геометрическому смыслу
определенный интеграл равен площади
криволинейной трапеции. Криволинейная
трапеция, ограниченная сверху кривой
![]() на отрезке
на отрезке
![]() ,
включает в свой состав криволинейную
трапецию, ограниченную сверху кривой
,
включает в свой состав криволинейную
трапецию, ограниченную сверху кривой
![]() .
Поэтому в таком же соотношении находятся
определенные интегралы.
.
Поэтому в таком же соотношении находятся
определенные интегралы.
Свойство 6. Если m
и M
наименьшее и наибольшее значение
функции
![]() на отрезке
на отрезке
![]() ,
то
,
то
 .
.
Д о к а з а т е л ь
с т в о. Так как
![]() ,
то по предыдущему свойству
,
то по предыдущему свойству

 .
.
Свойство 7. Теорема
о среднем. Если функция
![]() непрерывна на отрезке
непрерывна на отрезке
![]() ,
то найдется такая точка
,
то найдется такая точка
![]() ,
принадлежащая
,
принадлежащая
![]() ,
что
,
что
 .
.
Д о к а з а т е л ь
с т в о. Непрерывная на отрезке
![]() функция достигает своего наименьшего
m
и наибольшего М
значений. Поэтому
функция достигает своего наименьшего
m
и наибольшего М
значений. Поэтому
 .
.
Поделим это
равенство на b
a,
получим
 .
.
Функция
![]() непрерывная на
непрерывная на
![]() принимает любое значение между наименьшим
m
и наибольшим М
значениями и, следовательно, в некоторой
точке
принимает любое значение между наименьшим
m
и наибольшим М
значениями и, следовательно, в некоторой
точке
![]() принимает значения, равное
принимает значения, равное
 .
Откуда получаем
.
Откуда получаем
 .
.
|
Рис. 60 |
Геометрически
это означает, что для любой криволинейной
трапеции на отрезке
|

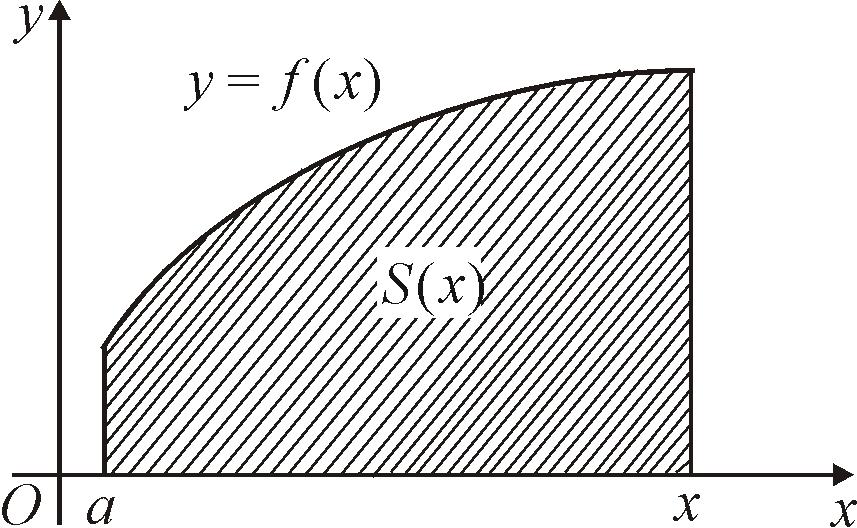
 (рис. 59).
(рис. 59).