3.11. Частные производные высших порядков
Частной производной
n-го
порядка называется частная производная
от частной производной (n1)-го
порядка. Например, пусть функция
зависит от двух переменных. Она имеет
две частные производные
и
.
Каждую из этих производных в свою
очередь можно продифференцировать по
каждой из независимых переменных и
получить четыре производные второго
порядка:
,
,
и
.
Данный процесс можно продолжать до тех
пор, пока частные производные существуют.
Теорема 3.5. Смешенные частные производные не зависят от порядка дифференцирования, если они являются непрерывными.
Например, покажем,
что совпадают смешанные частные
производные второго порядка для функции
.
Находим
,
.
,
.
3.12. Дифференциалы высших порядков
Дифференциалом n-го порядка называется дифференциал от дифференциала (n1)-го порядка, полученный в предположении, что дифференциалы независимых переменных постоянны.
Полный дифференциал
функция
равен
.
Используя определение, найдем дифференциал второго порядка.
.
Приведем подобные, получим
.
Для дифференциалов можно использовать операторную запись.
Для функции двух переменных дифференциалы второго и n-го порядка в операторной записи имеют вид соответственно
и
.
Дифференциал k-го
порядка функции n
переменных
имеет вид
.
Пример 3.15.
Записать дифференциал второго порядка
для функции
.
Находим
,
,
,
,
.
Запишем дифференциал
.
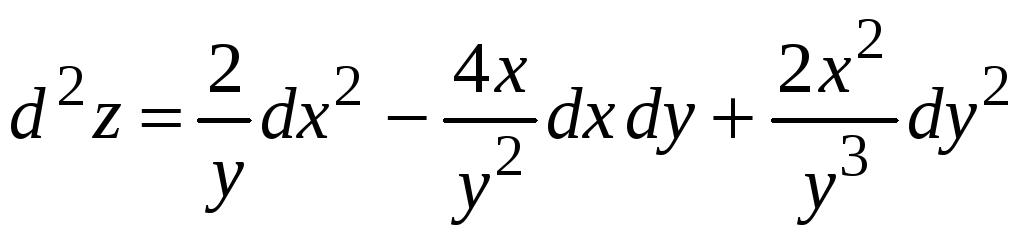3.13. Частные производные сложной функции нескольких переменных
Функция
называется сложной, если ее аргументы
являются в свою очередь функциями
каких-либо других переменных, например,
,
.
Пусть функции
,
и
являются непрерывными и дифференцируемыми.
Пусть переменная y
является постоянной (
),
а х изменяется
и получает приращение х.
Тогда функции
и
получают приращения по х
соответственно
.
Так как функция
является дифференцируемой, то ее
приращение можно представить как
линейное выражение относительно
приращений независимых переменных
,
где
и
бесконечно малые функции более высокого
порядка по сравнению
.
Найдем
.
Аналогично, в случае, когда х = const, а y получает приращение y
,
где
и
бесконечно малые функции более высокого
порядка по сравнению
.
.
Таким образом, в
случае сложной функции
,
,
формулы дифференцирования имеют вид
;
.
В частном случае,
когда
,
,
,
.
Если
,
,
то
.
Пример 3.16.
Найти частные производные сложной
функции
,
.
Находим
.
.
Пример 3.17.
Найти производную функции
,
,
.
Находим
.
Пример 3.18.
Найти производную функции
,
.
Находим
.
3.14. Производная функции, заданной неявно
Функция
называется заданной неявно, если она
задана уравнением
неразрешенным относительно z.
Например,
,
.
Уравнение
геометрически представляет поверхность
в трехмерном пространстве. Пусть на
этой поверхности имеются две точки
и
.
Приращение функции
при переходе от точки М
к точке
равняется
.
Будем считать, что
функция
является дифференцируемой. Тогда
можно представить в виде
,
где
бесконечно малые функции по сравнению
с
,
.
Найдем
.
Так как
и
стремятся к нулю при
,
то
.
Отсюда следует
.
Аналогично можно
получить формулу для производной по
второй переменной y
.
Таким образом,
формулы для нахождения частных производных
функции
,
заданной неявно, имеют вид
;
или более кратко можно записать
.
Неявная функция
одной переменной
задается уравнением
.
Формула для нахождения ее производной
имеет вид
или
.
Пример 3.19.
Найти производную функции
,
заданной уравнением
.
Находим
.
Пример 3.20.
Найти частные производные функции
,
заданной уравнением
.
Находим
.
.