2.3. Ускорение точки.

1. При векторном способе задания движения.

Предположим, что в момент времени скорость точки , а в момент .

Предел приращения скорости к приращению времени за которое произошло это приращение, при условии, что , называется ускорением точки в данный момент времени.

(9)

2. При координатном способе задания движения.

Вектор скорости точки

.

С учетом (9)

(*)

Но для вектора ускорения точки имеем

(**)

Сравнивая (*) и (**), получим

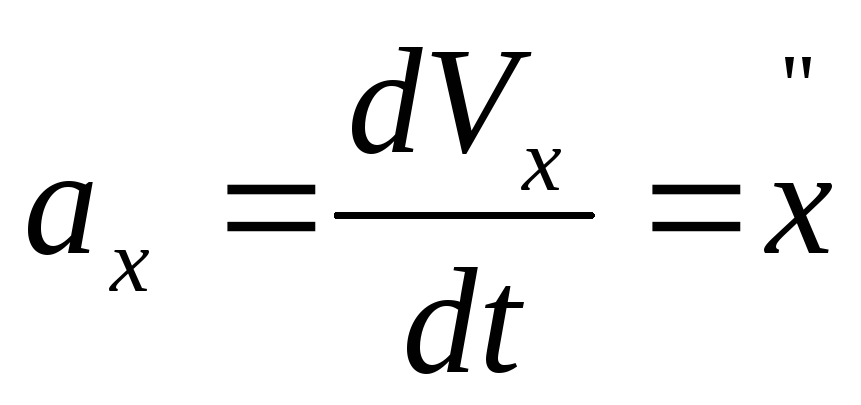
(10)

Модуль ускорения точки

. (11)

Направление вектора ускорения определяется направляющими косинусами:

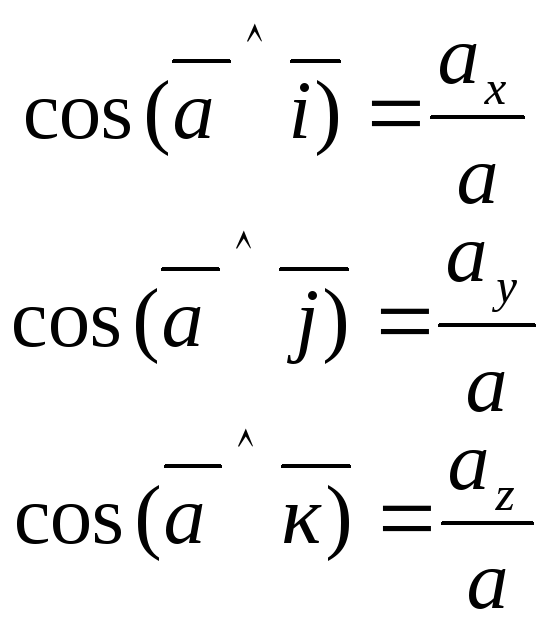
3. При естественном способе задания движения.

Пусть известна траектория точки.

Возьмем две близкие на траектории точки М и М₁ – .

Вектор перенесем в точку М и проведем плоскость через . Эта плоскость, называется соприкасающейся плоскостью.

Плоскость перпендикулярная соприкасающейся, называется нормальной плоскостью. Плоскость перпендикулярная нормальной и соприкасающейся плоскостям называется спрямляющей плоскостью.

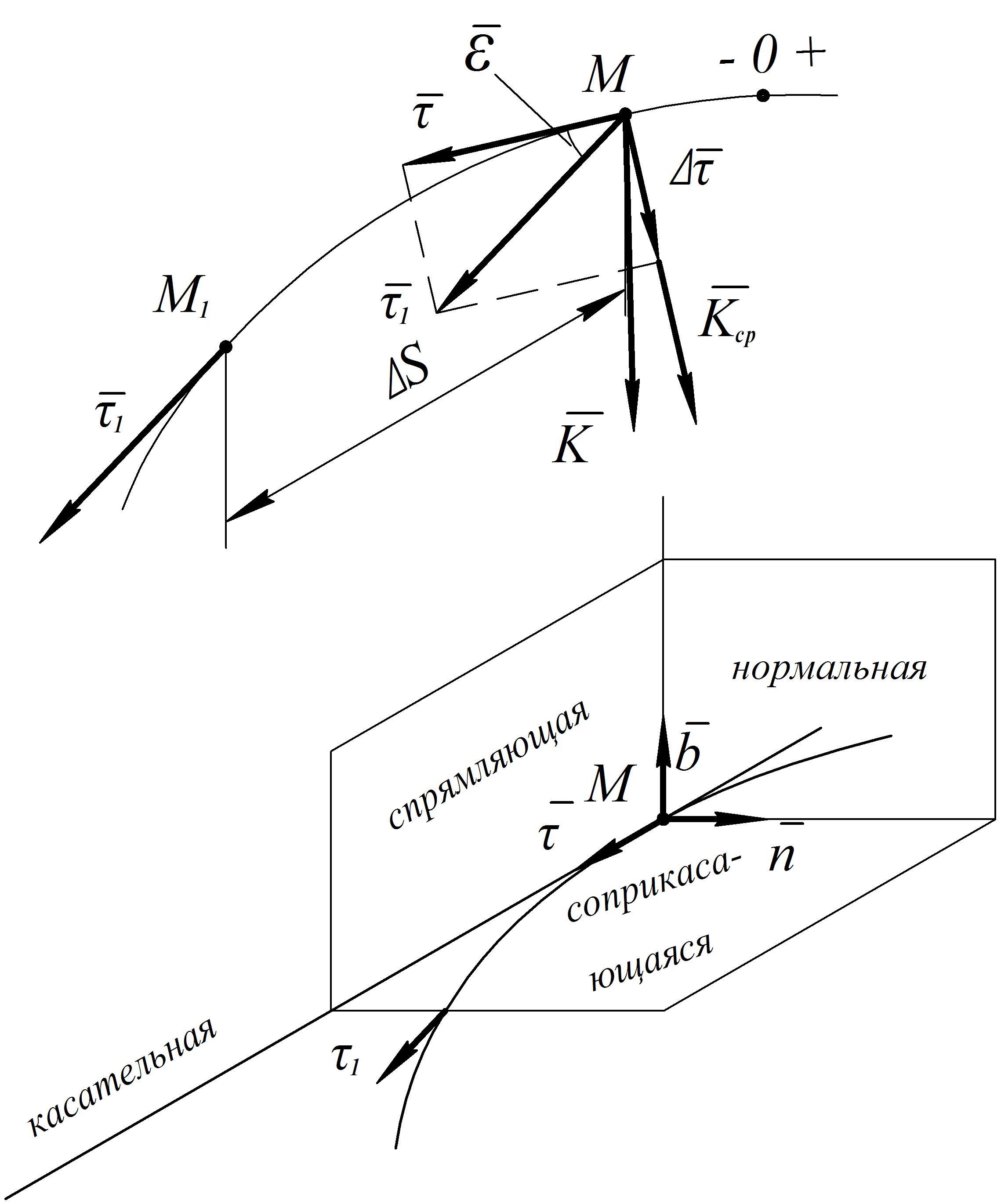
Рис.2.6

Три взаимно перпендикулярные плоскости:

нормальная, соприкасающая и спрямляющая образуют естественный трехгранник.

Линия пересечения нормальной и соприкасающейся плоскостей называется главной нормалью. Орт главной нормали – . Линия пересечения нормальной и спрямляющей плоскостей называется бинормалью траектории. Ось бинормали .

Три взаимно перпендикулярные оси: касательная, направленная в сторону возрастания дуговой координаты; главная нормаль, направленная в сторону вогнутости траектории; бинормаль, направленная по отношению к также, как ось z по отношению к осям х, y, называются естественными осями.

Угол между касательными в двух ближайших точках траектории называется углом смежности .

Кривизной кривой в точке М называется предел отношения угла смежности к абсолютному значению длины дуги ММ, между ближайшими точками траектории

₍₁₂₎

Радиусом кривизны в точке М называется величина, обратная кривизне:

. (13)

Получим формулу для вычисления ускорения точки М. Согласно выражению (8) имеем:

.

Продифференцируем по времени обе части этого равенства

(*)

Вычислим .

Так как направление по главной нормали, то .

Подставим в (*)

,

Ускорение точки лежит в соприкасающейся плоскости и определяется как векторная сумма касательного и нормального ускорений точки:

. (14)

Проекция ускорения на касательную определяется формулой:

. (15)

Касательное ускорение характеризует изменение скорости по величине. Оно равно нулю, когда величина скорости остается неизменной. Кроме того, оно обращается в нуль в те моменты времени, когда скорость достигает экстремальных значений.

Величина нормального ускорения определяется формулой:

, (16)

где – радиус кривизны.

Нормальное ускорение характеризует изменение скорости по направлению. Оно равно нулю при прямолинейном движении точки, а также в точках перегиба траектории, так как в обоих случаях радиус кривизны обращается в бесконечность. Кроме того, в точках где V=0.

Модуль ускорения вычисляется по формуле:

. (16)

Рис. 2.7

Направление ускорения:

Некоторые частные случаи движения точки.

1. Прямолинейное движение

.

Так как при прямолинейном движении скорость изменяется только численно, то делаем вывод, что касательное ускорение характеризует изменение скорости по численной величине.

2. Равномерное криволинейное движение

Равномерным называется такое движение, в котором численная величина скорости остается все время постоянной ():

Так как ускорение при равномерном движении появляется в результате изменения направления скорости, то нормальное ускорение характеризует изменение скорости по направлению. Получим закон движения.

Отсюда: .

Проинтегрируем:

Подставим пределы интегрирования:

В результате получим закон равномерного криволинейного движения:

3. Равномерное прямолинейное движение

следовательно,

4. Равнопеременное криволинейное движение

Равнопеременным называется такое криволинейное движение, при котором касательное ускорение остается величиной постоянной:

, проинтегрируем

но проинтегрируем

– закон равнопеременного криволинейного движения.