
- •Глава IV Числовые последовательности п. 1 Определение и примеры
- •Способы задания последовательности
- •Последовательности бывают:
- •Бмп (бесконечно малые последовательности);
- •3. Неограниченные;
- •Пример. Последовательность ограничена, но не является бмп.
- •П. 2 Свойства бмп
- •П. 3 Сходящиеся последовательности
- •П. 4 Арифметические свойства пределов
- •П. 5 Свойства пределов, связанные с неравенствами
- •П. 6 Принцип компактности и принцип полноты
- •П. 7 Число e
П. 3 Сходящиеся последовательности
Определение
1. Последовательность
![]() называется сходящейся,
если
называется сходящейся,
если
![]() ,
где
,
где
![]() - БМП, а число
- БМП, а число
![]() .
Тогда число
.
Тогда число
![]() называется пределом
последовательности
называется пределом
последовательности
![]() .
Обозначается
.
Обозначается
![]() (
(![]() при
при
![]() ,
стремящимся к бесконечности, стремится
к (или равно)
,
стремящимся к бесконечности, стремится
к (или равно)
![]() ).
).
Определение
1*. Последовательность
![]() сходится к
сходится к
![]() ,
т.е.
,
т.е.
![]() если если для любого положительного
(эпсилон)
найдется номер, зависящий от ,
такой, что, как только n>N
выполняется соотношение
если если для любого положительного
(эпсилон)
найдется номер, зависящий от ,
такой, что, как только n>N
выполняется соотношение
![]() :
:
(**)
![]() .
.
Покажем, что определения 6 и 6* эквивалентны.
Пусть
![]() в смысле определения 6. Тогда
в смысле определения 6. Тогда
![]() ,
где
,
где
![]() - БМП. Следовательно,
- БМП. Следовательно,
![]() - БМП, тогда выполняется соотношение
(*), т.е.
- БМП, тогда выполняется соотношение
(*), т.е.
![]() .
Получим соотношение (**).
.
Получим соотношение (**).
Теперь
пусть
![]() в смысле определения 6*. Тогда выполняется
соотношение (**). Полагая
в смысле определения 6*. Тогда выполняется
соотношение (**). Полагая
![]() ,
получим
,
получим
![]() ,
которая является БМП в соответствие с
соотношением (*). Тогда
,
которая является БМП в соответствие с
соотношением (*). Тогда
![]() .
.
Теорема 1. О единственности предела
Если
последовательность
![]() сходится, то она имеет единственный
предел.
сходится, то она имеет единственный
предел.
Доказательство:
![]() .
Пусть последовательность
.
Пусть последовательность
![]() имеет два предела, т.е.
имеет два предела, т.е.
![]() ,
,
![]() ,
,
![]() для определенности. Так как
для определенности. Так как
![]() то имеет место соотношение (**), т.е.
начиная с некоторого номера
то имеет место соотношение (**), т.е.
начиная с некоторого номера
![]() .
Так как
.
Так как
![]() то выполняется (**), т.е. начиная с некоторого
номера
то выполняется (**), т.е. начиная с некоторого
номера
![]()
![]() .
Пусть
.
Пусть
![]() тогда,
начиная с номера
тогда,
начиная с номера
![]()
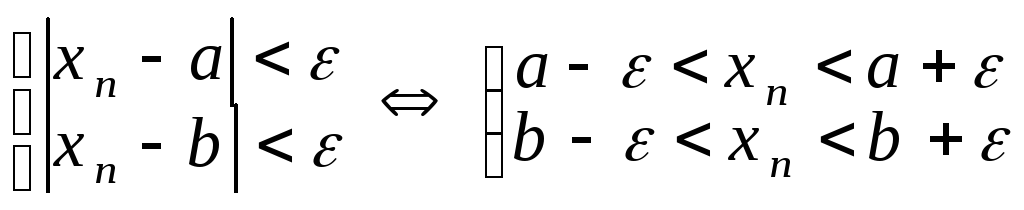 .
Пусть
.
Пусть
![]() Тогда пересечение этих двух множеств,
задаваемых неравенствами, пусто, т.е.
нашлось, по крайней мере, одно
Тогда пересечение этих двух множеств,
задаваемых неравенствами, пусто, т.е.
нашлось, по крайней мере, одно
![]() для которого не выполняется (**). Это
означает, что предела не существует.
для которого не выполняется (**). Это
означает, что предела не существует.
Теорема 2. Теорема Вейерштрасса - необходимое условие сходимости
Если последовательность сходится, то она ограничена.
Доказательство:
Пусть
последовательность
![]() сходится, тогда имеет место соотношение
(**), т.е. начиная с некоторого номера
сходится, тогда имеет место соотношение
(**), т.е. начиная с некоторого номера
![]() ,
,
![]() .
Положим
.
Положим
![]() ,
тогда
,
тогда
![]() .
Рассмотрим
.
Рассмотрим
![]() ,т.е.
,т.е.
![]() ,что
озна- чает ограниченность последовательности
,что
озна- чает ограниченность последовательности
![]() .
.
Теорема 3. Признак Больцано-Вейерштрасса.
Если последовательность монотонно возрастает (убывает) и ограничена сверху(снизу), то она сходится.
Доказательство:
Пусть
последовательность
![]() монотонно возрастает (
монотонно возрастает (![]() )
и ограничена (
)
и ограничена (![]() ).
Тогда из условия ограниченности следует,
что
).
Тогда из условия ограниченности следует,
что
![]() - непустое ограниченное сверху множество.
Следовательно, по теореме о ТВГ (глава
III,
п. 4) множество
- непустое ограниченное сверху множество.
Следовательно, по теореме о ТВГ (глава
III,
п. 4) множество
![]() ,
значит, и последовательность
,
значит, и последовательность
![]() имеет ТВГ.
имеет ТВГ.
Обозначим
![]() и покажем, что
и покажем, что
![]() .
.
В
силу определения ТВГ имеем
![]()
![]() .
Кроме того, последова- тельность
.
Кроме того, последова- тельность
![]() монотонно возрастает, поэтому найдется
такой номер
монотонно возрастает, поэтому найдется
такой номер
![]() ,
что
,
что
![]() т.е.
т.е.
![]() .
Следовательно,
.
Следовательно,
![]() или
или
![]() .
Таким образом, существует такой номер
.
Таким образом, существует такой номер
![]() ,
начиная с которого
,
начиная с которого
![]() .
.
Пример.
Последовательность
![]() монотонно возрастает, но не ограничена,
следовательно,
монотонно возрастает, но не ограничена,
следовательно,
![]() расходится.
расходится.
Пример.
Последовательность
![]() ограничена, но не является монотонной,
следовательно, расходится.
ограничена, но не является монотонной,
следовательно, расходится.
Пример.
Пусть
![]() и
и
![]()
![]() ,...
или
,...
или
![]() (*). Последовательность
(*). Последовательность
![]() монотонно возрастает и ограничена
сверху, например, числом
монотонно возрастает и ограничена
сверху, например, числом
![]() .
Покажем это ММИ.
.
Покажем это ММИ.
Пусть
![]() .
Тогда
.
Тогда
![]()
![]() .
Тогда существует
.
Тогда существует
![]() .
Возведем (*) в квадрат и перейдем к пределу
при
.
Возведем (*) в квадрат и перейдем к пределу
при
![]() :
:
![]() ,
т.е.
,
т.е.
![]() .
Таким образом,
.
Таким образом,
![]() .
.
П. 4 Арифметические свойства пределов
Теорема
1.
Пусть последовательности
![]() и
и
![]() сходятся, тогда сходится и последовательность
сходятся, тогда сходится и последовательность
![]() ,
причем
,
причем
![]() .
.
Доказательство:
Так
как
![]() и
и
![]() ,
то
,
то
![]() ,
,
![]() ,
где
,
где
![]() и
и
![]() - БМП. Рассмотрим
- БМП. Рассмотрим
![]() ,
причем
,
причем
![]() - БМП. Следовательно,
- БМП. Следовательно,
![]() .
.
Следствие. Сумма любого конечного числа сходящихся последовательностей, является сходящейся последовательностью, предел которой равен сумме соответствующих пределов.
Теорема
2.
Если
![]() ,
,
![]() (пределы
последовательностей xп
и
yп
равны a
и
b
соответственно), то
(пределы
последовательностей xп
и
yп
равны a
и
b
соответственно), то
![]() .
.
Доказательство:
В
силу определения предела последователь-
ности имеем
![]()
![]() где
где
![]() ,
,
![]() - БМП. Рассмотрим
- БМП. Рассмотрим
![]()
![]() ,
при этом
,
при этом
![]() - БМП. Следовательно,
- БМП. Следовательно,
![]()
Теорема
3.
Если пределы последовательностей xп
и
yп
равны a
и
b
соответственно для любого натурального
числа n
и yп
≠0,
b≠0
(![]() ,
,
![]()
![]() ),
то
),
то
![]() .
.
Доказательство:
Докажем сначала лемму.
Лемма.
Если последовательность
![]() сходится
сходится
![]() ,
то последовательность
,
то последовательность
![]() - ограничена.
- ограничена.
Пусть
![]() .
Тогда имеет место соотношение (**). Пусть
в (**)
.
Тогда имеет место соотношение (**). Пусть
в (**)
![]() т.е.
т.е.
![]() .
Тогда существует номер
.
Тогда существует номер
![]() ,
начиная с которого
,
начиная с которого
![]() или
или
![]() .
Следовательно,
.
Следовательно,
![]() или
или
![]() .
Пусть
.
Пусть
![]() .
Тогда
.
Тогда
![]() .
▲
.
▲
Рассмотрим
![]()
![]() .
Так как
.
Так как
![]() - БМП, а
- БМП, а
![]() - ограничена, то
- ограничена, то
![]() - БМП. Таким образом,
- БМП. Таким образом,
![]() .
.
