
- •Partea I şirul de experimente independente lucrare de laborator nr. 1 Formula Bernulli. Teorema limită locală a lui Moivre – Laplace
- •Lucrare de laborator nr. 2 Aplicarea Teoremei Integrale Moivre-Laplace. Teorema lui Bernulli.
- •Probleme tipice care conduc la aplicarea teoremei lui Moivre-Laplace.
- •Lucrare de laborator nr. 3 Distribuţia/repartiţia Poisson ca aproximare a distribuţiei binomiale.
- •Anexă b, Funcţia de repartiţie normală normată Laplace (n(0,1))
- •Valorile funcţiei
- •Anexa c. Repartiţia Poisson
Lucrare de laborator nr. 3 Distribuţia/repartiţia Poisson ca aproximare a distribuţiei binomiale.
Deseori există probleme în care este necesară determinarea probabilităţii Pn(k) cînd n iau valori mari, iar valorile p şi q sunt mici. Formula lui Bernulli pentru n cu valoare mare conduce la calcule foarte complicate. Formula asimptotică Moivre-Laplace pentru p şi q cu valori mici generează rezultate destul de eronate. Apare întrebarea găsirii unei formule asimptotice pentru cazul în care p ia valori mici în timp ce n ia valori destul de mari.
Remintim, că în prima
lucrare de laborator, am arătat că dacă p
este mic, iar n
suficient de mare
pentru evaluarea lui
![]() ,
se foloseşte formula lui Poisson
,
se foloseşte formula lui Poisson
Să
considerăm variabila aleatoare
Cu
aceste notaţii putem scrie
Deci,
notând
![]() care
urmează o repartiţie binomială. Dacă n creşte necontenit, pe
când p descreşte, astfel încât
care
urmează o repartiţie binomială. Dacă n creşte necontenit, pe
când p descreşte, astfel încât
![]() rămâne
constant, atunci repartiţia binomială tinde către repartiţia
Polsson.
rămâne
constant, atunci repartiţia binomială tinde către repartiţia
Polsson.
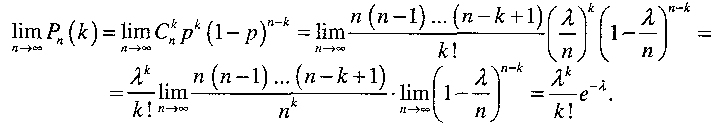
![]() ,
avem
,
avem![]()
Astfel, când n creşte arbitrar, iar valoarea lui p scade arbitrar, şi în acelaşi timp produsul np rămîne constant, se poate demonstra că distribuţia binomială tinde spre cea Poisson, adică
![]() ,
k=1,2,…., unde λ=np
(3.1)
,
k=1,2,…., unde λ=np
(3.1)
Iată de ce prin legea Poisson poate fi aproximativ înlocuită distribuţia binomială, în cazul în care probabilitatea p a evenimentului aleator A în fiecare experiment este mică, iar numărul n de experimente realizate este unul relativ mare, adică are loc egalitatea aproximativă
![]() (3.2)
(3.2)
Valoarea P (k) creşte odată cu creşterea lui k de la 0 la k0=[λ0] iar în cazul ulterioarei creşterii a lui k, P (k) scade. Dacă λ – este număr întreg, atunci P (k) are două valori maxime: pentru k0=λ şi k0=λ-1.
Fie
că variabila
aleatoare
Definiţie:
Sistemul de egalităţi
De
obicei, repartiţia unei variabile aleatoare discrete se scrie sub
forma unui tabel în
care prima linie conţine toate valorile posibile, iar în a doua
linie sub fiecare valoare este
trecută probabilitatea cu care
(Aici I
fiind o mulţime cel mult numerabilă de indici).
Definiţie:
Tabelul (1) se
numeşte repartiţia
sau distribuţia
variabilei aleatoare
![]() ia
valorile.
ia
valorile.
![]() Una
şi aceeaşi valoare
Una
şi aceeaşi valoare
![]() poate
să corespundă,
în general, la
câteva
evenimente
elementare
ale spaţiului
poate
să corespundă,
în general, la
câteva
evenimente
elementare
ale spaţiului
![]() Totalitatea
acestor evenimente elementare formează un eveniment, care este
Totalitatea
acestor evenimente elementare formează un eveniment, care este
![]() Probabilitatea acestui eveniment o notăm cu
Probabilitatea acestui eveniment o notăm cu
![]()
![]() defineşte
distribuţia
sau
repartiţia
variabilei aleatoare
defineşte
distribuţia
sau
repartiţia
variabilei aleatoare
![]()
![]() ia
această valoare:
ia
această valoare: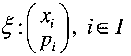 (1)
(1)![]()
Funcţia
de repartiţie a variabilei aleatoare
Mai
sus am văzut că variabila
aleatoare discretă
este caracterizată de repartiţia
ei. Acest mod de a defini o variabilă aleatoare nu
este valabil
pentru o variabilă
aleatoare continuă,
deoarece nu este cu putinţă să enumerăm toate valorile
posibile ale unei astfel de variabile.
Acest fapt ne arată că trebuie găsit un mod comun de
definire a ambelor tipuri de variabile aleatoare.
Aşadar, pentru a caracteriza
cantitativ această repartiţie este comod de a ne folosi nu de
probabilitatea evenimentului
Definiţie: Se numeşte funcţie
de repartiţie (sau de distribuţie) a variabilei
aleatoare
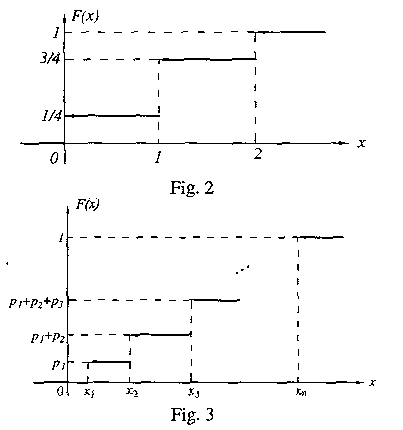
Geometric această egalitate poate fi interpretată
astfel: funcţia de repartiţie
Exemplu: Moneda este aruncată de doiiă
ori. Spaţiul evenimentelor elementare este
Câmpul de evenimente
Remarcăm că evenimentul
Deci,
Graficul acestei ftincţii
este în trepte (vezi fig. 2).
Cunoscând tabelul de repartiţie al unei variabile
aleatoare discrete
![]() ,ci
de probabilitatea evenimentului
,ci
de probabilitatea evenimentului
![]() ,
unde x este variabilă reală. Evident că
probabilitatea evenimentului
,
unde x este variabilă reală. Evident că
probabilitatea evenimentului
![]() depinde de x,
adică ea este o
funcţie de X,
pe care o
vom nota cu
depinde de x,
adică ea este o
funcţie de X,
pe care o
vom nota cu
![]()
![]() aplicaţia
aplicaţia
![]() definită
prin egalitatea
definită
prin egalitatea![]()
![]() este probabilitatea ca variabila aleatoare
este probabilitatea ca variabila aleatoare
![]() să ia valori care pe o axă numerică se reprezintă la stânga
punctului x (fig.l).
să ia valori care pe o axă numerică se reprezintă la stânga
punctului x (fig.l).![]()
![]() esie totalitatea tuturor submulţirailor lui
esie totalitatea tuturor submulţirailor lui
![]() Numărul
Numărul
![]() de apariţii ale stemei este o
funcţie care asociază fiecărui
de apariţii ale stemei este o
funcţie care asociază fiecărui
![]() un număr real .
un număr real .
![]() poate fi prezentat după cum urmează
poate fi prezentat după cum urmează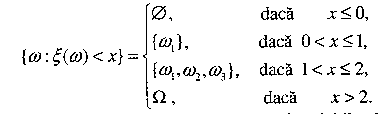
![]() este
variabila aleatoare.
Funcţia de
repartiţie a acestei variabile aleatoare este
este
variabila aleatoare.
Funcţia de
repartiţie a acestei variabile aleatoare este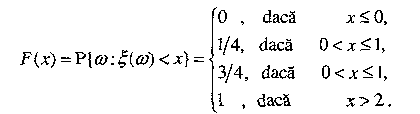
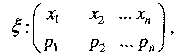

putem afla şi funcţia de
repartiţie a acestei variabile care are expresia
adică funcţia de repartiţie în punctul x
este egală cu suma
probabilităţilor valorilor
Exemplu: Doua semnale pot
ajunge la receptor la
întâmplare şi independent unul de celălalt în
intervalul
Fie x1 şi x2
momentele sosirilor la receptor a celor
două semnale.
Spaţiul evenimentelor elementare este
Câmpul de evenimente
pentru orice x aparţine lui
Pentru simplificarea scrierii vom adopta notaţia
![]()
![]() situate la stânga lui X.
Graficul acestei funcţii de repartiţie este prezentat
în fig. 3.
situate la stânga lui X.
Graficul acestei funcţii de repartiţie este prezentat
în fig. 3.![]()
![]()
![]() este generat de submuiţimi cuadrabile ale pătratului
este generat de submuiţimi cuadrabile ale pătratului
![]() Dacă
Dacă
![]() ,
atunci
,
atunci
![]() unde
unde
![]() este aria submulţimii
este aria submulţimii
![]() .
Fie
.
Fie![]() -
timpul dintre cele două
momente de sosire,
adică
-
timpul dintre cele două
momente de sosire,
adică
![]() unde
unde
![]() Observăm
că funcţia este
Observăm
că funcţia este![]() variabilă aleatoare, deoarece mulţimea
variabilă aleatoare, deoarece mulţimea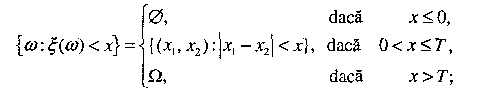
![]() (vezi
fig. 4, a). Aflăm funcţia de repartiţie a lui
(vezi
fig. 4, a). Aflăm funcţia de repartiţie a lui
![]()
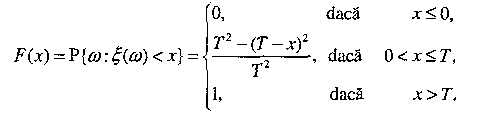
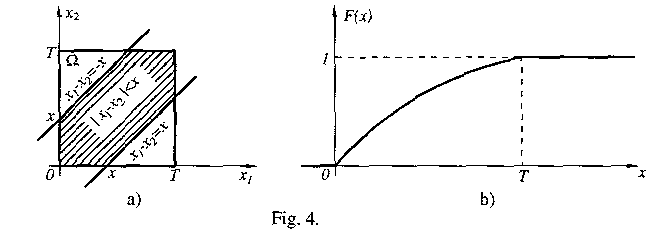 Graficul
funcţiei
Graficul
funcţiei
![]() se poate vedea în (fig. 4, b)
se poate vedea în (fig. 4, b)![]()
Sarcina 3.1. Staţia telefonică deserveşte n utilizatori. Probabilitatea ca orice abonat a apelat comutatorul într-o perioadă de timp t este egală cu p: a) determinaţi numărul cel mai probabil de abonaţi care apelează comutatorul într-o periodă de timp t, şi probabilitatea lui. Comparaţi rezultatele calculelor obţinute cu ajutorul calculelor de distribuţie Poisson şi distribuţiei binomiale; b) Care este probabilitatea că într-o periodă de timp t vor apela nu mai mult de k abonaţi? Fie n = 800, p = 0,005, k = 10. Soluţie: a) Deoarece λ = np = 0,005 * 800 = 4, atunci numărul cel mai probabil de abonaţii care doresc să apeleze într-un interval de timp t, pot fi doar două valori: 3 şi 4. Probabilităţile lor
sunt respectiv egale cu
![]() .
.
Folosind
formula lui Poisson în conformitate cu Tabelele
din Anexa C,
obţinem
![]() .
.
Valoarea exactă ![]() ;
;
b)
probabilitatea ca numărul de abonaţi ξ,
care doresc să apeleze într-un interval de timp, va fi nu mai mare
de 10
este egală cu:
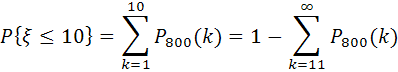
În virtutea formulei
(3.2) ![]() (k=0,1,2,3…),
astfel
(k=0,1,2,3…),
astfel
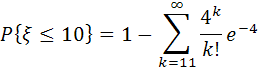
Dar
![]() >
>![]() +
+![]() +
+![]() =
=![]() =0,00276
=0,00276
Pe de altă
parte,
![]() <
<![]() +
+![]() +
+![]() (1+
(1+![]() +….)=
+….)=![]() =0,00284.
=0,00284.
Astfel, 0,99716≤![]() ≤0,99724
≤0,99724
Sarcina 3.2. În rezultatul efectuării experimentului, evenimentul aleator A se produce cu probabilitatea p. Testul se repetă de n ori. Care este probabilitatea ca evenimentul se va produce de k = 0,1,2 ... ori? Fie ξ numărul de producere a evenimentului A. Determinaţi valoarea funcţiei de distribuţie a variabilei aleatoare ξ în punctele xk=0,1,2,….
Fie p = 0,001, n = 2000, atunci λ = 0,001 * 2000 = 2 şi înlocuind în formula (3.1) şi folosind totodată formula
F(x)=![]() =
=![]() ,
,
unde inegalitate k<x indică că sumarea se răsfrînge asupra tuturor acelor valori ale lui k, care sînt mai mici ca x, vom obţine următoarele probabilităţi enumerate în Tabelul 6.
Tabelul 6
|
k |
P(k) |
Funcţia de distribuţie |
k |
P(k) |
Funcţia de distribuţie |
|
0 |
0,1353 |
0 |
6 |
0,0121 |
0,9834 |
|
1 |
0,2707 |
0,1353 |
7 |
0,0034 |
0,9955 |
|
2 |
0,2707 |
0,4060 |
8 |
0,0009 |
0,9989 |
|
3 |
0,1804 |
0,6767 |
9 |
0,0002 |
0,9998 |
|
4 |
0,0902 |
0,8571 |
10 |
|
0,99995 |
|
5 |
0,0361 |
0,9437 |
11 |
|
1 |
SARCINĂ Pentru a efectua lucrarea de laborator nr. 3 - a obţine abilităţi de lucru cu repartiţia lui Poisson şi a funcţiei de distribuţie/repartiţie F(x).
Date iniţiale. Fie că se efectuează n experimente independente şi fiecare dintre ele pune în evidenţă un eveniment A cu aceeaşi probabilitate de apariţie p. Se ştie că evenimentul A poate să se realizeze exact de k ori.
Este necesar de precăutat şi executat toate sarcinile 3.1-3.2 pentru datele variantului de lucru.
Pentru efectuarea calculelor este necesară definirea parametrilor iniţiali. În continuare sunt prezentate succint problemele care urmează să fie rezolvate. Alăturat găsiţi descrierea datelor iniţiale.
Determinaţi
-
repartiţia Poisson.
Datele iniţiale sunt: n - numărul de experimente, p - probabilitatea de succes la fiecare experiment a evenimentului aleator A care se realizează exact de k ori, k – numărul de apariţii a evenimentului aleator A.
-
funcţia de repartiţie/distribuţie;
Datele iniţiale sunt: n - numărul de experimente, p - probabilitatea de succes la fiecare experiment a evenimentului aleator A care se realizează exact de k ori, k – numărul de apariţii a evenimentului aleator A.
Notă: În procesul de calcul, se va apela la Tabelele din Anexa C. La ieşire urmează să fie obţinute:
-
valorea probabilităţii
-
funcţia de repartiţie F(x), şi graficul ei.
Datele iniţiale pentru sarcina 3.1
|
Nr. var. |
n |
p |
k |
|
1 |
1000 |
0,0004 |
5 |
|
2 |
2000 |
0,001 |
6 |
|
3 |
1000 |
0,0015 |
10 |
|
4 |
1000 |
0,0005 |
8 |
|
5 |
800 |
0,003 |
15 |
|
6 |
105 |
0,00008 |
20 |
|
7 |
3500 |
0,0005 |
12 |
|
8 |
1250 |
0,001 |
10 |
|
9 |
2500 |
0,005 |
10 |
|
10 |
1700 |
0,001 |
12 |
|
11 |
1300 |
0,001 |
11 |
|
12 |
5000 |
0,001 |
10 |
|
13 |
22000 |
0,00015 |
13 |
|
Nr. var. |
n |
p |
k |
|
14 |
2800 |
0,0005 |
9 |
|
15 |
3500 |
0,0002 |
10 |
|
16 |
1350 |
0,002 |
10 |
|
17 |
1000 |
0,0004 |
7 |
|
18 |
2000 |
0,001 |
3 |
|
19 |
1000 |
0,0015 |
8 |
|
20 |
1000 |
0,0005 |
10 |
|
21 |
800 |
0,003 |
8 |
|
22 |
105 |
0,00008 |
15 |
|
23 |
3500 |
0,0005 |
10 |
|
24 |
1250 |
0,001 |
6 |
|
25 |
2500 |
0,005 |
6 |
|
26 |
1700 |
0,001 |
8 |
|
27 |
1300 |
0,001 |
5 |
|
28 |
5000 |
0,001 |
9 |
|
29 |
22000 |
0,00015 |
10 |
|
30 |
2800 |
0,0005 |
5 |
|
31 |
3500 |
0,0002 |
4 |
|
32 |
1350 |
0,002 |
7 |
|
33 |
1000 |
0,0004 |
10 |
|
34 |
2000 |
0,001 |
8 |
|
35 |
1000 |
0,0015 |
6 |
|
36 |
1000 |
0,0005 |
11 |
|
37 |
800 |
0,003 |
12 |
|
38 |
105 |
0,00008 |
16 |
|
39 |
3500 |
0,0005 |
14 |
|
40 |
1250 |
0,001 |
12 |
|
41 |
2500 |
0,005 |
14 |
|
42 |
1700 |
0,001 |
10 |
|
43 |
1300 |
0,001 |
8 |
|
44 |
5000 |
0,001 |
9 |
|
45 |
22000 |
0,00015 |
12 |
|
46 |
2800 |
0,0005 |
11 |
|
47 |
3500 |
0,0002 |
14 |
|
48 |
1350 |
0,002 |
15 |
Datele iniţiale pentru sarcina 3.2
|
Nr. var. |
n |
p |
|
1 |
1300 |
0.001 |
|
2 |
22000 |
0.00015 |
|
3 |
2800 |
0.005 |
|
4 |
1350 |
0.002 |
|
5 |
5000 |
0.001 |
|
6 |
3500 |
0.0002 |
|
7 |
1700 |
0.001 |
|
8 |
2500 |
0.005 |
|
9 |
1250 |
0.001 |
|
10 |
1000 |
0.0015 |
|
11 |
800 |
0.003 |
|
12 |
3500 |
0.0005 |
|
13 |
106 |
0.00008 |
|
14 |
10000 |
0,0005 |
|
15 |
2000 |
0.001 |
|
16 |
1000 |
0,0004 |
|
17 |
13000 |
0.001 |
|
18 |
20000 |
0.00015 |
|
19 |
28000 |
0.005 |
|
20 |
13500 |
0.002 |
|
21 |
50000 |
0.001 |
|
22 |
35000 |
0.0002 |
|
23 |
17000 |
0.001 |
|
24 |
25000 |
0.005 |
|
25 |
12500 |
0.001 |
|
26 |
10000 |
0.0015 |
|
27 |
8000 |
0.003 |
|
28 |
32000 |
0.0005 |
|
29 |
1060 |
0.00008 |
|
30 |
15000 |
0,0005 |
|
31 |
3000 |
0.001 |
|
32 |
4000 |
0,0004 |
|
33 |
5300 |
0.001 |
|
34 |
27000 |
0.00015 |
|
35 |
3800 |
0.005 |
|
36 |
3350 |
0.002 |
|
37 |
4000 |
0.001 |
|
38 |
6500 |
0.0002 |
|
39 |
4700 |
0.001 |
|
40 |
3500 |
0.005 |
|
41 |
3250 |
0.001 |
|
42 |
2000 |
0.0015 |
|
43 |
500 |
0.003 |
|
44 |
6500 |
0.0005 |
|
45 |
206 |
0.00008 |
|
46 |
50000 |
0,0005 |
|
47 |
7000 |
0.001 |
|
48 |
8000 |
0,0004 |
Anexa Al. Funcţia de repartiţie normală normată (Laplace) N(0,1)
|
x |
0.0000 |
0,0100 |
0,0200 |
0,0300 |
0.0400 |
0,0500 |
0,0600 |
0,0700 |
0,0800 |
0,0900 |
||||
|
0,0 |
0,5000 |
0,5040 |
0,5080 |
0,5120 |
0,5160 |
0,5199 |
0,5239 |
0,5279 |
0,5319 |
0,5359 |
||||
|
0,1 |
0,5398 |
0,5438 |
0,5478 |
0.5517 |
0,5557 |
0,5596 |
0,5636 |
0,5675 |
0,5714 |
0.5753 |
||||
|
0,2 |
0,5793 |
0,5832 |
0,5871 |
0,5910 |
0,5948 |
0,5987 |
0,6026 |
0,6064 |
0,6103 |
0,6141 |
||||
|
0,3 |
0,6179 |
0,6217 |
0.6255 |
0,6293 |
0,6331 |
0,6368 |
0,6406 |
0,6443 |
0,6480 |
0,6517 |
||||
|
0,4 |
0,6554 |
0,6591 |
0,6628 |
0,6664 |
0,6700 |
0,6736 |
0,6772 |
0,6808 |
0,6844 |
0,6879 |
||||
|
0,5 |
0,6915 |
0,6950 |
0,6985 |
0,7019 |
0,7054 |
0,7088 |
0,7123 |
0,7157 |
0,7190 |
0,7224 |
||||
|
0,6 |
0,7257 |
0,7291 |
0,7324 |
0,7357 |
0,7389 |
0,7422 |
0,7454 |
0,7486 |
0,7517 |
0,7549 |
||||
|
0,7 |
0,7581 |
0,7611 |
0,7642 |
0,7673 |
0,7704 |
0,7734 |
0,7764 |
0,7794 |
0,7823 |
0,7852 |
||||
|
0,8 |
0,7881 |
0,7910 |
0,7939 |
0,7967 |
0,7995 |
0,8023 |
0,8051 |
0,8079 |
0,8106 |
0,8133 |
||||
|
0,9 |
0,8159 |
0,8186 |
0,8212 |
0,8238 |
0,8264 |
0,8289 |
0,8315 |
0,8340 |
0,8365 |
0,8389 |
||||
|
1,0 |
0,8413 |
0,8438 |
0,8461 |
0,8485 |
0,8508 |
0,8531 |
0,8554 |
0,8577 |
0,8599 |
0,8621 |
||||
|
1,1 |
0,8643 |
0,8665 |
0,868'6 |
0,8708 |
0,8729 |
0,8749 |
0,8770 |
0,8790 |
0,8810 |
0,8830 |
||||
|
1,2 |
0,8849 |
0,8869 |
0,8888 |
0,8907 |
0,8925 |
0,8944 |
0.8962 |
0,8980 |
0,8997 |
0,9015 |
||||
|
1,3 |
0,9032 |
0,9049 |
0,9066 |
0,9082 |
0,9099 |
0,9115 |
0,9131 |
0,9147 |
0,9162 |
0,9177 |
||||
|
1.4 |
0,9192 |
0,9207 |
0,9222 |
0,9236 |
0,9251 |
0,9265 |
0,9279 |
0,9292 |
0,9306 |
0,9319 |
||||
|
1.5 |
0,9332 |
0,9345 |
0,9357 |
0,9370 |
0,9382 |
0,9394 |
0.9406 |
0,9418 |
0,9429 |
0,9441 |
||||
|
1,6 |
0,9452 |
0,9463 |
0,9474 |
0,9484 |
0,9495 |
0,9505 |
0,9515 |
0,9525 |
0,9535 |
0,9545 |
||||
|
1,7 |
0,9554 |
0,9564 |
0,9573 |
0,9582 |
0,9591 |
0,9599 |
0,9608 |
0,9616 |
0,9625 |
0,9633 |
||||
|
1,8 |
0,9641 |
0,9649 |
0,9656 |
0,9664 |
0,9671 |
0,9678 |
0,9686 |
0,9693 |
0,9699 |
0,9706 |
||||
|
1,9 |
0,9713 |
0,9719 |
0,9726 |
0,9732 |
0,9738 |
0,9744 |
0,9750 |
0,9756 |
0.9761 |
0,9767 |
||||
|
2,0 |
0,9773 |
0,9778 |
0,9783 |
0,9788 |
0,9793 |
0,9798 |
0,9803 |
0,9808 |
0,9812 |
0,9817 |
||||
|
2,1 |
0,9821 |
0,9826 |
0,9830 |
0,9834 |
0,9838 |
0,9842 |
0,9846 |
0,9850 |
0,9854 |
0,9857 |
||||
|
2,2 |
0,9861 |
0,9864 |
0,9868 |
0,9871 |
0,9875 |
0,9878 |
0,9881 |
0,9884 |
0,9887 |
0,9890 |
||||
|
2,3 |
0,9893 |
0,9896 |
0,9898 |
0,9901 |
0,9904 |
0,9906 |
0,9909 |
0.99!) |
0,9913 |
0,9916 |
||||
|
2,4 |
0,9918 |
0,9920 |
0,9922 |
0,9925 |
0.9927 |
0,9929 |
0,9931 |
0,9932 |
0,9934 |
0,9936 |
||||
|
2,5 |
0,9938 |
0.9940 |
0,9941 |
0,9943 |
0„9945 |
0,9946 |
0,9948 |
0.9949 |
0,9951 |
0,9952 |
||||
|
2,6 |
0,9953 |
0.9955 |
0,9956 |
0,9957 |
0,9959 |
0,9960 |
0,9961 |
0,9962 |
0,9963 |
0,9964 |
||||
|
2,7 |
0,9965 |
0,9966 |
0,9967 |
0,9968 |
0,9969 |
0,9970 |
0,9971 |
0,9972 |
0.9973 |
0,9974 |
||||
|
2,8 |
0,9974 |
0,9975 |
0,9976 |
0,9977 |
0,9977 |
0,9978 |
0.9979 |
0,9979 |
0,9980 |
0,9981 |
||||
|
2,9 |
0,9981 |
0,9982 |
0,9983 |
0,9983 |
0,9984 |
0.9984 |
0,9985 |
0,9985 |
0,9986 |
0,9986 |
||||
|
3.0 |
0,99865 |
0,99869 |
0,99874 |
0,99878 |
0,99882 |
0,99886 |
0,99889 |
0,99893 |
0,99896 |
0,99900 |
||||
|
3,1 |
0,99903 |
0,99906 |
0,99910 |
0,99913 |
0,99915 |
0,99918 |
0,99921 |
0,99924 |
0,99926 |
0,99929 |
||||
|
3,2 |
0,99931 |
0,99934 |
0,99936 |
0,99938 |
0,99940 |
0,99942 |
0,99944 |
0,99946 |
0,99948 |
0,99950 |
||||
|
3,3 |
0,99952 |
0,99953 |
0,99955 |
0.99957 |
0,99958 |
0,99960 |
0,99961 |
0,99962 |
0,99964 |
0,99965 |
||||
|
3,4 |
0,99966 |
0.99967 |
0,99969 |
0,99970 |
0,99971 |
0,99972 |
0.99973 |
0,99974 |
0,99975 |
0,99976 |
||||
|
3,5 |
0,99977 |
0,99978 |
0,99978 |
0,99979 |
0,99980 |
0,99981 |
0,99981 |
0,99982 |
0,99983 |
0,99983 |
||||
Anexa A2. Densitatea de probabilitate a repartiţiei normale normate N(0,1)
![]()
|
X |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
0,0 |
0,3989 |
3989 |
3989 |
3988 |
3986 |
3984 |
3982 |
3980 |
3977 |
3973 |
|
0,1 |
3970 |
3965 |
3961 |
3956 |
3951 |
3945 |
3939 |
3932 |
3925 |
3918 |
|
0,2 |
3910 |
3902 |
3894 |
3885 |
3876 |
3867 |
3857 |
3847 |
3836 |
3825 |
|
0.3 |
3814 |
3802 |
3790 |
3778 |
3765 |
3752 |
3739 |
3726 |
3712 |
3697 |
|
0,4 |
3683 |
3668 |
3653 |
3637 |
3621 |
3605 |
3589 |
3572 |
3555 |
3538 |
|
0.5 |
3521 |
3503 |
3485 |
3467 |
3448 |
3429 |
3410 |
3391 |
3372 |
3352 |
|
0.6 |
3332 |
3312 |
3292 |
3271 |
3251 |
3230 |
3209 |
3187 |
3166 |
3144 |
|
0.7 |
3123 |
3101 |
3079 |
3056 |
3034 |
3011 |
2989 |
2966 |
2943 |
2920 |
|
0.8 |
2897 |
2874 |
2850 |
2827 |
2803 |
2780 |
2756 |
2732 |
2709 |
2685 |
|
0,9 |
2661 |
2637 |
2613 |
2589 |
2565 |
2541 |
2516 |
2492 |
2468 |
2444 |
|
1,0 |
0,2420 |
2396 |
2371 |
2347 |
2323 |
2299 |
2275 |
2251 |
2227 |
2203 |
|
l.l |
2179 |
2155 |
2131 |
2107 |
2083 |
2059 |
2036 |
2012 |
1989 |
1965 |
|
1.2 |
1942 |
1919 |
1895 |
Î872 |
1849 |
1826 |
1804 |
1781 |
1758 |
1736 |
|
1,3 |
1714 |
1691 |
1669 |
1647 |
1626 |
1604 |
1582 |
1561 |
1539 |
1518 |
|
1.4 |
1497 |
1476 |
1456 |
1435 |
1415 |
1394 |
1374 |
1354 |
1334 |
1315 |
|
1.5 |
1295 |
1276 |
1257 |
1238 |
1219 |
1200 |
1182 |
1163 |
1145 |
1127 |
|
1.6 |
1109 |
1092 |
1074 |
1057 |
1040 |
1023 |
1006 |
0989 |
0973 |
0957 |
|
1.7 |
0940 |
0925 |
0909 |
0893 |
0878 |
0863 |
0848 |
0833 |
0818 |
0804 |
|
!,8 |
0790 |
0775 |
0761 |
0748 |
0734 |
0721 |
0707 |
0694 |
0681 |
0669 |
|
1,9 |
0656 |
0644 |
0632 |
0620 |
0608 |
0596 |
0584 |
0573 |
0562 |
0551 |
|
2,0 |
0.0540 |
0529 |
0519 |
0508 |
0498 |
0488 |
0478 |
0468 |
0459 |
0449 |
|
2,1 |
0440 |
0431 |
0422 |
0413 |
0404 |
0396 |
0387 |
0379 |
0371 |
0363 |
|
2,2 |
0355 |
0347 |
0339 |
03.32 |
0325 |
0317 |
0310 |
0303 |
0297 |
0290 |
|
2,3 |
0283 |
0277 |
0270 |
0264 |
0258 |
0252 |
0246 |
0241 |
0235 |
0229 |
|
2,4 |
0224 |
0219 |
0213 |
0208 |
0203 |
0198 |
0191 |
0189 |
0184 |
0180 |
|
2,5 |
0175 |
0171 |
0167 |
0)63 |
0158 |
0154 |
0151 |
0147 |
0143 |
0139 |
|
2,6 |
0136 |
0132 |
0129 |
0126 |
0122 |
0119 |
0116 |
0113 |
0110 |
0107 |
|
2,7 |
0104 |
0101 |
0099 |
0096 |
0093 |
0091 |
0088 |
0086 |
0084 |
0081 |
|
2,8 |
0079 |
0077 |
0075 |
0073 |
0071 |
0069 |
0067 |
0065 |
0063 |
0061 |
|
2,9 |
0060 |
0058 |
0056 |
0055 |
0053 |
0051 |
0050 |
0048 |
0047 |
0046 |
|
3,0 |
0,0044 |
0043 |
0042 |
0040 |
0039 |
0038 |
0037 |
0036 |
0035 |
0034 |
|
3,1 |
0033 |
0032 |
0031 |
0030 |
0029 |
0028 |
0027 |
0026 |
0025 |
0025 |
|
3,2 |
0024 |
0023 |
0022 |
0022 |
002! |
0020 |
0020 |
0019 |
0018 |
0018 |
|
3,3 |
0017 |
0017 |
0016 |
0016 |
0015 |
0015 |
0014 |
0014 |
0013 |
0O13 |
|
3,4 |
0012 |
0012 |
0012 |
0011 |
0011 |
0010 |
0010 |
0010 |
0009 |
0009 |
|
3,5 |
0009 |
0008 |
0008 |
0008 |
0008 |
0007 |
0007 |
0007 |
0007 |
0006 |
|
3.6 |
0006 |
0006 |
0006 |
0005 |
0005 |
0005 |
0005 |
0005 |
0005 |
0004 |
|
3,7 |
0004 |
0004 |
0004 |
0004 |
0004 |
0004 |
0003 |
0003 |
0003 |
0003 |
|
3.8 |
0003 |
0003 |
0003 |
0003 |
0003 |
0002 |
0002 |
0002 |
0002 |
0002 |
|
3,9 |
0002 |
0002 |
0002 |
0002 |
0002 |
0002 |
0002 |
0002 |
0001 |
0001 |
Anexă
A,
Funcţia de repartiţie normală normată Laplace N(0,1))
Valorile
funcţiei
х Ф(х) х Ф(х) х Ф(х) х Ф(х) 0.00 0.00000 0.85 0.30234 1.70 0.45543 2.55 0.49461 0.05 0.01994 0.90 0.31594 1.75 0.45994 2.60 0.49534 0.10 0.03983 0.95 0.32894 1.80 0.46407 2.65 0.49598 0.15 0.05962 1.00 0.34134 1.85 0.46784 2.70 0.49653 0.20 0.07926 1.05 0.35314 1.90 0.47128 2.75 0.49702 0.25 0.09871 1.10 0.36433 1.95 0.47441 2.80 0.49744 0.30 0.11791 1.15 0.37493 2.00 0.47725 2.85 0.49781 0.35 0.13683 1.20 0.38493 2.05 0.47982 2.90 0.49813 0.40 0.15542 1.25 0.39435 2.10 0.48214 2.95 0.49841 0.45 0.17364 1.30 0.40320 2.15 0.48422 3.00 0.49865 0.50 0.19146 1.35 0.41149 2.20 0.48610 3.20 0.49931 0.55 0.20884 1.40 0.41924 2.25 0.48778 3.40 0.49966 0.60 0.22575 1.45 0.42647 2.30 0.48928 3.60 0.499841 0.65 0.24215 1.50 0.43319 2.35 0.49061 3.80 0.499928 0.70 0.25804 1.55 0.43943 2.40 0.49180 4.00 0.499968 0.75 0.27337 1.60 0.44520 2.45 0.49286 4.50 0.499997 0.80 0.28814 1.65 0.45053 2.50 0.49379 5.00 0.5
![]()
