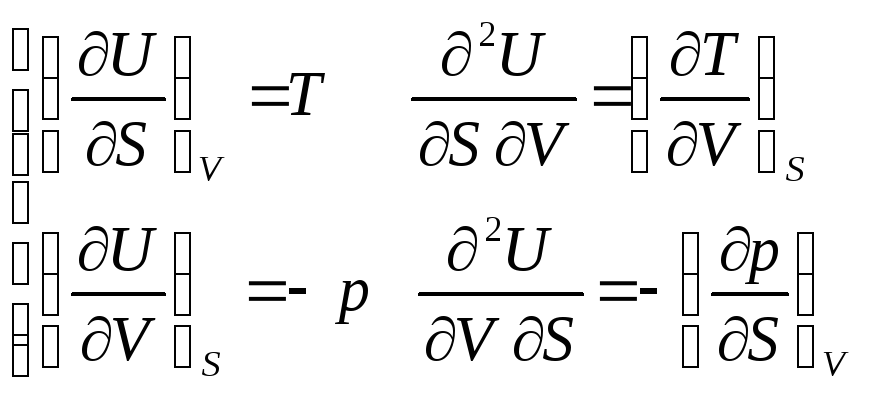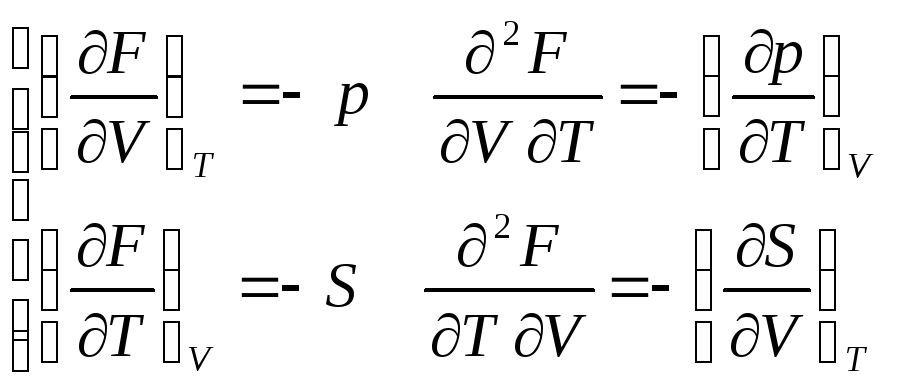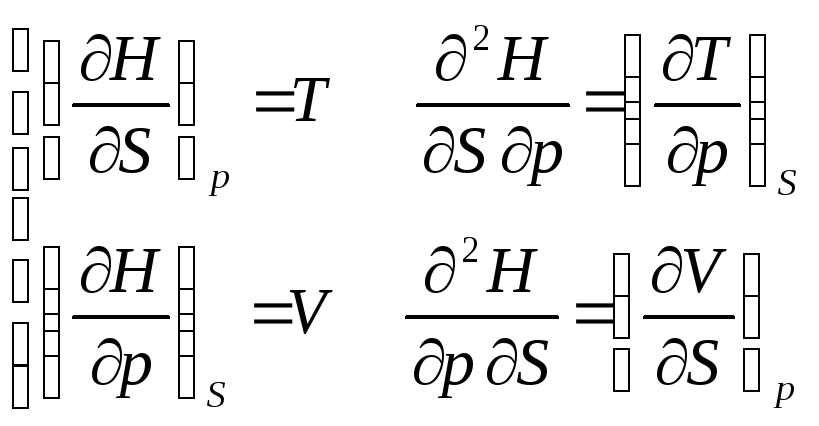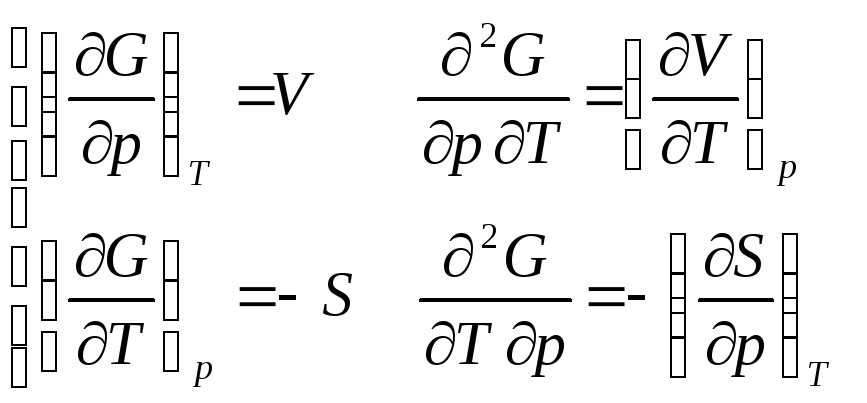время как при статистическом подходе энтропия определена точно и равна нулю, когда макросостояние реализуется только одним микросостоянием. Еще до получения этого результата Больцманом и Планком, Нернст в 1906 году сформулировал теорему, согласно которой при стремлении температуры к абсолютному нулю, энтропия стремится к значению, не зависящему от способа приближения системы к абсолютному нулю:
. (5.7.1)
Отсюда следует, что возможные изменения конфигурации системы при абсолютном нуле происходят без изменения энтропии. Нернст предложил положить универсальную константу равной нулю
(5.7.2)
и энтропия получает абсолютное начало.
Теорему Нернста формулируют именно как вывод о недостижимости абсолютного нуля: невозможно достижение абсолютного нуля за счет отвода теплоты из системы посредством реальных процессов, - и называют третьим началом термодинамики.
Последовательную физическую трактовку теорема Нернста получила в рамках квантовой статистической физики.
§8. Термодинамические функции
Все расчёты в термодинамике осуществляются при помощи так называемых термодинамических функций (потенциалов). Каждому набору независимых параметров соответствует своя термодинамическая функция – функция состояния системы. Изменения этих функций в различных процессах определяют либо совершаемую работу, либо получаемое количество теплоты.
Для
того, чтобы определить термодинамические
функции, перепишем первое начало
термодинамики с учётом 2-го начала
.
Для обратимых процессов имеем:
,
откуда
,
и следовательно,
(5.8.1)
- это соотношение определяет термодинамическую функцию, называемую внутренней энергией (U) .
Естественными переменными U являются S и V, т.е. U=U(S,V).
Тогда можно записать
(5.8.2)
И
з
этого следует, что, зная зависимость
U(S,V),
можно рассчитать T
и P.
В
отсутствии теплообмена (δQ
= 0, т.е.
)
, (5.8.3)
т.е. при адиабатической изоляции убыль внутренней энергии равна работе системы.
В
изолированной системе при V=Const.
.
В равновесии U
– минимальна.
При обратимом изотермическом процессе первое начало термодинамики можно записать в виде
, (5.8.4)
где F=U-TS – свободная энергия (потенциал Гельмгольца).
При
необратимом процессе
получаем
,
т.е. убыль свободной энергии определяет
верхний предел той работы, которую может
совершить система при изотермическом
процессе. Выпишем полный дифференциал
F
с учётом выражения для dU
. (5.8.5)
Таким образом, естественными переменными свободной энергии являются V и T, т.е. F=(V,T). Видно что
. (5.8.6)
Если
процесс происходит при V=Const,
T=Const,
то dF=0
для обратимого процесса и
для
необратимого процесса.
Таким образом, при V=Const, T=Const равновесное состояние достигается при минимуме свободной энергии.
Если процесс происходит изобарно, т.е. при постоянном давлении (р=Const), то из первого начала термодинамики имеем
, (5.8.7)
где H=U+PV – энтальпия системы.
Энтальпия показывает, какое количество теплоты поступает в систему при изобарических условиях.
Полный дифференциал H равен
(5.8.8)
Таким образом, естественными переменными H являются S, p. H=H(S,p). Видно, что
. (5.8.9)
В
изолированной системе при p=Const
(dH=0
в равновесном состоянии). Таким образом,
в этом случае равновесие достигается
при минимальном значении H.
Мы видим, что в качестве естественных переменных для термодинамических потенциалов выступают величины V, P, T, S: U=U(S,V), F=F(V,T), H=H(S,P). Для симметрии не хватает некоторой функции состояния, зависящей от переменных P и T. Обозначим эту функцию G=G(P,T). По аналогии с другими термодинамическими функциями, функция G должна иметь минимум при P=Const, T=Const в состоянии равновесия. Перепишем первое начало термодинамики в виде
(5.8.10)
При p=const и T=Const
,
т.е.
(5.8.11)
- термодинамическая функция Гиббса.
Полный дифференциал G равен
(5.8.12)
Таким образом G=G(р,T).
Видно, что
. (5.8.13)
Заметим, что частные производные термодинамических функций по их естественным переменным определяют остальные переменные из совокупности переменных V, р, S, T.
Учитывая свойства смешанных производных (их независимость от порядка дифференцирования) получим:
|
для U |
|
, откуда |
|
|
Для F |
|
, откуда |
|
|
Для H |
|
, откуда |
|
|
Для G |
|
, откуда |
|
;
;
;
.
Приведенные соотношения носят название соотношения Мксвелла.
Соотношения Максвелла позволяют по одним термодинамическим зависимостям определять другие, а анализ термодинамических функций на экстремум определяет условия равновесия системы.