Глава 1. Элементы линейной алгебры
1.1. Понятие линейного пространства
В курсе аналитической геометрии и векторной алгебры мы изучали понятия арифметического и геометрического вектора и поняли, что по своим алгебраическим свойствам, если ограничиться операциями сложения и умножения на число, эти объекты совершенно одинаковы. Это побуждает нас обобщить понятие вектора, рассматривая его исключительно в плане свойств линейных операций (т.е. сложения и умножения на число), с тем, чтобы частные виды векторов (например, геометрические или арифметические векторы) можно было изучать в рамках единой теории. Отчасти мы уже это и делали, рассматривая понятия базиса на множествах геометрических или арифметических векторов.
Обобщение понятия вектора достигается через определение линейного пространства.
Определение 1.1
Линейным
пространством
называется произвольное множество
такое, что для любых двух его элементов
и
однозначно определен элемент
,
называемый суммой
и
,
для любого элемента
и любого вещественного числа
однозначно определен элемент
,
называемый результатом умножения
на число
,
причем для операций сложения и умножения
на число по определению имеют место
следующие свойства:
-
-
-
существует такой элемент
,
что для каждого
-
для каждого
существует элемент
,
называемый противоположным
к
такой, что
-
-
-
-
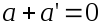
(В формулах, написанных
выше, под
понимаются произвольные элементы
,
а под
произвольные вещественные числа.)
Элементы множества
называют векторами,
а само это множество часто называют
векторным
пространством.
Элемент
при этом называют нулевым
вектором
данного пространства, а вектор
такой , что
,
называют противоположным
к вектору
.
Договоримся впредь знак умножения вектора на число опускать.
Можно было бы определить точно так же умножение вектора на комплексное число. Мы в нашем курсе ограничимся по существу только умножением на вещественные числа и, желая подчеркнуть это, будем называть только что определенное линейное пространство вещественным линейным пространством.
Примеры.
1) Множества геометрических и арифметических
векторов фиксированной размерности
образуют линейные пространства, которые
мы будем обозначать соответственно
и
.
Заметим, что строя конкретный пример линейного пространства, мы должны доказывать свойства операций (1) - (8), которые в определении 1.1 постулируются. И в прошлом семестре мы именно доказывали эти свойства для геометрических и арифметических векторов (опуская, впрочем, подробности).
2) Множество матриц
фиксированного порядка размера
относительно
операций сложения и умножения на число
есть линейное пространство, которое мы
будем обозначать
.
Нулевым вектором этого пространства
является нулевая матрица, а вектором,
противоположным данному, матрице
,
служит матрица
.
3) Рассмотрим на первый взгляд несколько необычный пример линейного пространства.
Пусть
- множество всех функций, непрерывных
на отрезке
числовой прямой.
Для двух произвольных
функций
определим их сумму как функцию
так, что
(обычное «поточечное» сложение функций, известное из школьной алгебры в виде процедуры сложения «графиков», причем, как известно из курса математического анализа, сумма непрерывных функций непрерывна).
Для любой функции
и произвольного вещественного
введем новую функцию
(результат
умножения
на
)
так, что
(также известная из школы процедура «растяжения» графика в заданное число раз, преобразующая непрерывную функцию в непрерывную).
Легко видеть, что
для функции
,
тождественно равной нулю (и, очевидно,
непрерывной) на отрезке
имеют место соотношения:
Все свойства операций
сложения и умножения на число в данном
случае легко проверяются, и мы получаем,
что множество всех функций, непрерывных
на отрезке, является линейным пространством.
В этом пространстве нулевая функция
играет роль нулевого вектора, а функция
, график которой получается отражением
графика
относительно оси абсцисс, - роль
противоположного к
вектора.
Таким образом, на непрерывную функцию можно смотреть как на вектор, то есть, как на элемент соответствующего векторного пространства.
Рассмотрим теперь некоторые следствия из определения линейного пространства.