КУРС «МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ»

Содержание:

1. Основные формы и задачи ЛП 1

2. Типовые задачи линейного программирования 2

2.1 Задача о планировании производства 2

2.2 Задача о рационе 3

2.3 Задача прикрепления потребителей к поставщикам (транспортная задача) 4

3. Графический метод решения задач 6

3.1 Графически решаются задачи: 6

3.2 Допустимая область: 6

3.3 Число оптимальных планов: 7

3.4 Этапы решения: 7

Определение. Линейное программирование (ЛП) – область математического программирования, предназначенная для решения оптимизационных задач, в которых целевая функция (критерий эффективности) и функции ограничений являются линейными.

1. Основные формы и задачи лп

Общая задача ЛП (ОЗЛП):

Целевая функция или

Система ограничений

или

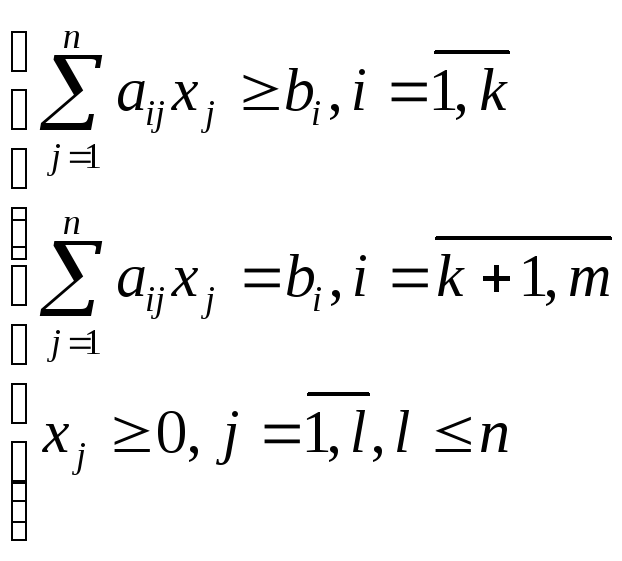
Стандартная (симметричная) задача ЛП:

Целевая функция или

Система ограничений (k=m, l=n)

или

Каноническая (основная) задача ЛП:

Целевая функция

Система ограничений (k=0, l=n)

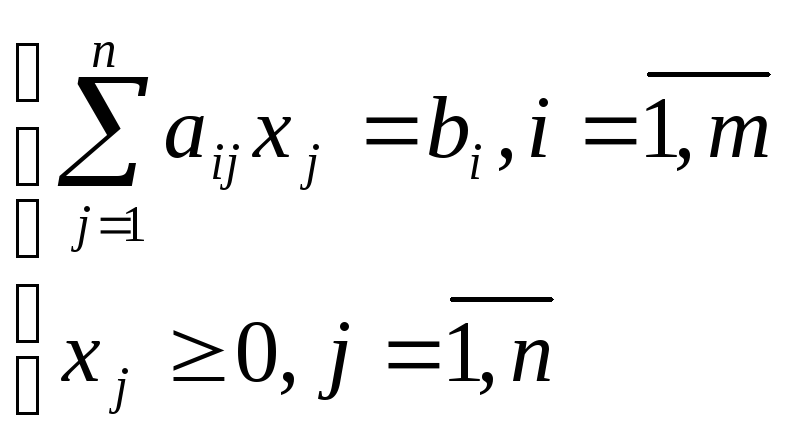
Стандартная форма – большое число прикладных моделей сводится к этой форме.

Каноническая форма – основные варианты симплекс-метода разработаны для этой формы.

Указанные три формы ОЗЛП эквивалентны – каждая из них может с помощью несложных преобразований может быть приведена к любой из них. Любую задачу ЛП можно привести к каноническому виду.

Способы перехода к каноническому виду

1)Сведение задач минимизации к задачам максимизации:

2)Переход от ограничений-неравенств к ограничениям-равенствам.

3)Замена отрицательных переменных неотрицательными

2. Типовые задачи линейного программирования

   1. Задача о планировании производства

Предприятие производит изделия трех видов U₁, U₂, U₃. По каждому виду изделия предприятию спущен план, по которому оно обязано выпустить не менее b₁ единиц изделия U₁, не менее b₂ единиц изделия U₂ и не менее b₃ единиц изделия U₃. План может быть перевыполнен, но в определенных границах; условия спроса ограничивают количества произведенных единиц каждого типа: β₁, β₂, β₃ единиц. На изготовление изделий идет какое-то сырье; всего имеется четыре вида сырья s₁, s₂, s₃,, s₄ , причем запасы ограничены числами γ₁, γ₂, γ₃, γ₃ единиц каждого вида сырья. Теперь надо указать, какое количество сырья каждого вида идет на изготовление каждого вида изделий. Обозначим a_ij количество единиц сырья вида s₁ (i = 1, 2, 3, 4), потребное на изготовление одной единицы изделия U_j (j = 1, 2, 3). Первый индекс у числа a_ij – вид изделия, второй – вид сырья. Значения a_ij сведены в таблицу (матрицу).

Сырье	Изделия
	U1	U2	U3
s 1	a11	a21	a31
s 2	a12	a22	a32
s 3	a13	a23	a33
s 4	a14	a24	a34

При реализации единица изделия U₁ приносит предприятию прибыль с₁, U₂ – прибыль с₂, U₃ – прибыль с₃. Требуется так спланировать производство (сколько и каких изделий производить), чтобы план был выполнен или перевыполнен (но при отсутствии «затоваривания»), а суммарная прибыль обращалась бы в максимум.

Запишем задачу в форме задачи линейного программирования. Элементами решения будут х₁, х₂, х₃ – количества единиц изделий U₁, U₂, U₃, которые мы произведем. Обязательность выполнения планового задания запишется в виде трех ограничений-неравенств:

Отсутствие излишней продукции (затоваривания) даст нам еще три ограничения-неравенства:

Кроме того, нам должно хватить сырья. Соответственно четырем видам сырья будем иметь четыре ограничения-неравенства:

Прибыль, приносимая планом (х₁, х₂, х₃), будет равна

L= с₁х₁+ с₂ х₂+ с₃ х₃.

Таким образом, мы снова получили задачу линейного программирования: найти такие неотрицательные значения переменных х₁, х₂, х₃,, чтобы они удовлетворяли ограничениям – неравенствам и одновременно обращали в максимум линейную функцию этих переменных:

.

В более общем виде задача формулируется следующим образом.

Пусть некоторое предприятие производит n типов товаров, затрачивая при этом m типов ресурсов. Известны следующие параметры:

• a_ij – количество i-го ресурса, необходимое для производства единичного количества j-го товара, a_ij≥0 (i = 1,…,m, j = 1,…,n);

• b_i – запас i-го ресурса на предприятии, b_i≥0;

• с_j – цена единичного количества j-го товара, с_j≥0.

Предполагается, что технология производства линейна, то есть затраты ресурсов растут прямо пропорционально объему производства. Пусть число х_j показывает планируемый объем производства j-го товара. Тогда допустимым является только такой набор производимых товаров х=(х₁, …, х_n), при котором суммарные затраты каждого i-го ресурса не превосходят его запаса:

. (I)

Кроме того, имеем следующие естественные ограничения:

. (II)

Стоимость набора товаров х выражается величиной

(III)

Задача планирования производства ставится следующим образом: среди всех векторов х, удовлетворяющих условиям (I), (II), найти такой, при котором величина (III) принимает наибольшее значение.