Алгебраические свойства

не замкнуто относительно деления двух целых чисел (например, 1/2). Следующая таблица иллюстрирует несколько основных свойств сложения и умножения для любых целых a, b и c.

	сложение	умножение
замкнутость:	a + b   — целое	a × b   — целое
ассоциативность:	a + (b + c)  =  (a + b) + c	a × (b × c)  =  (a × b) × c
коммутативность:	a + b  =  b + a	a × b  =  b × a
существование нейтрального элемента:	a + 0  =  a	a × 1  =  a
существование противоположного элемента:	a + (−a)  =  0	a  ≠  ±1  ⇒  1/a не является целым
дистрибутивность умножения относительно сложения:	a × (b + c)  =  (a × b) + (a × c)

На языке абстрактной алгебры первые пять вышеперечисленных свойств сложения говорят о том, что является абелевой группой относительно бинарной операции сложения, и, следовательно, также циклической группой, так как каждый ненулевой элемент может быть записан в виде конечной суммы 1 + 1 + … 1 или (−1) + (−1) + … + (−1). Фактически, является единственной бесконечной циклической группой по сложению в силу того, что любая бесконечная циклическая группа изоморфна группе .

Первые четыре свойства умножения говорят о том, что  — коммутативный моноид по умножению. Однако стоит заметить, что не каждое целое имеет противоположное по умножению, например, нет такого x из , что 2x = 1, так как левая часть уравнения чётна, а правая нечётна. Из этого следует, что не является группой по умножению, а также не является полем. Наименьшее поле, содержащее целые числа, — множество рациональных цисел ().

Совокупность всех свойств таблицы означает, что является коммутативным кольцом с единицей относительно сложения и умножения.

Обычное деление не определено на множестве целых чисел, но определено так называемое деление с остатком: для любых целых a и b, , существует единственный набор целых чисел q и r, что a = bq + r и , где |b| — абсолютная величина (модуль) числа b. Здесь a — делимое, b — делитель, q — частное, r — остаток. На этой операции основан алгоритм Евклида нахождения наибольшего общего делителя двух целых чисел.

Рациональные числа (Q), их сложение, вычитание, умножение и деление. Сравнение рациональных чисел.

Рациональные числа – это числа, которые можно представить в виде дроби , где m и n – целые числа, n ? 0. Пример: ; ; ; 1,01; 12 и т.д. Все целые числа являются рациональными.

Действительно, любое целое число n можно представить в виде дроби . Например, целое число 18 – это . Две дроби считаются равными, если . Пример: = , так как 3 • 2 = 6 • 1. Очевидно, что дроби равны. На этом свойстве основано сокращение дробей. Для того чтобы сократить дробь, находим общий делитель числителя и знаменателя и на этот делитель делим числитель и знаменатель - полученная дробь будет равна исходной. Пример: Сократить дробь . Над рациональными числами операции сложения, умножения и деления определены следующим образом: 1. Операция сложения:. Пример: . 2. Операция умножения: . Пример: . 3. Операция деления:, то есть, делитель «переворачиваем» Пример: . При сравнении рациональных чисел применяют следующие правила: 1. Всякое положительное рациональное число всегда больше всякого отрицательного рационального числа. 2. Если два числа положительны, то число больше , если , для отрицательных - наоборот. Пример: , так как 3 • 6 > 5 • 2.

Иррациональные числа. Сравнение иррациональных и рациональных чисел.

Иррациональные числа. Числа целые, дробные, десятичные конечные и десятичные периодические носят общее название рациональных чисел; десятичные бесконечные дроби непериодические называются иррациональными числами²⁾. Первые служат мерою величин, соизмеримых с единицею, вторые—мерою величин, несоизмеримых с единицею.

Иррациональное число считается известным (или данным), если указан способ, посредством которого можно находить любое число его десятичных знаков.

Два иррациональных числа (как и два рациональных) считаются равными, если они произошли от измерения одною и тою же единицею двух равных величин; из двух неравных чисел то считается большим, которое произошло от измерения большей величины. Две равные величины, конечно, должны содержать в себе одинаковое число целых единиц, одинаковое число десятых долей, одинаковое число сотых долей и т. п., поэтому равные иррациональные числа должны быть выражены одинаковыми цифрами³⁾. Большая же величина должна содержать в себе большее число целых или — при равенстве целых—большее   число   десятых,   или — при  равенстве целых и десятых — большее число, сотых и т. д. Напр., число 2,745037... больше числа 2,745029..., так как в первом 6-я цифра выражает число большее, чем 6-я цифра во втором, при тождественности всех предыдущих цифр.

Иррациональные числа могут быть положительными и отрицательными, смотря по тому, измеряют ли они величины, считаемые положительными, или величины, считаемые отрицательными.

186. Приближенные значения иррационального числа. Пусть нам дано какое-нибудь иррациональное число α ⁴⁾, т. е. пусть указан способ, посредством которого мы можем получить сколько угодно цифр числа α (этим способом может быть, напр., то правило, посредством которого мы находим приближенные квадратные корни с точностью до ¹/₁₀   до   ¹/₁₀₀   до   ¹/₁₀₀₀ и т. д.). Положим, мы нашли такие 5 цифр числа α:

α = 1,4142...

Возьмем из этих цифр несколько первых, напр, цифры 1,41, а остальные отбросим. Тогда мы получим приближенное значение числа α, причем это значение будет с недостатком, так как 1,41 < α. Если последнюю из удержанных нами цифр увеличим на 1, т. е. вместо 1,41 возьмем 1,42, то получим тоже приближенное значение числа α, но с избытком. Обыкновенно из двух приближенных значений, из которых одно с недостатком, другое с избытком, берут значение с недостатком, если первая из отброшенных цифр менее 5, и значение с избытком, если эта цифра больше 5.

187. Определение действий над иррациональными числами. Пусть α и β будут какие-нибудь данные положительные иррациональные числа. Если эти числа даны, то это значит, что мы можем найти их приближенные значения с любою точностью. Пусть, напр., приближенные значения чисел α и β, взятые с  недостатком, будут такие (мы берем приближенные значения √3  и √2 ):

	до 0,1	до 0,01	до 0,001	до 0,0001
для числа α .....	1,7	1,73	1,732	1,7320
для числа β .....	1,4	1,41	1,414	1,4142

(Соответствующие приближенные значения с избытком получаются из этих чисел посредством усиления последнего десятичного знака на 1.)

Тогда: а) сложить α и β  значит найти число, которое было бы

больше каждой из сумм: 1,7 + 1,1 . . . . =3,1 1,73 + 1,41 . . . =3,14 1,732+1,414  . . .=3,146 1,7320+1,4142 . . =3,1462

и меньше каждой из сумм:  1,8+1,6. . . .  =3,3 1,74+1,42. . .   =3,16 1,733 + 1,415 . .  =3,146 1,7321 + 1,4143 . .=3,1464

т. е. сложить числа α и β — значит найти такое третье число, которое было бы больше суммы любых приближенных их значении, взятых с недостатком, но меньше суммы любых приближенных значении, взятых с избытком.

б) Беря приближенные значения чисел α и β, указанные сейчас, мы можем сказать, что произведение α β есть число, которое

больше каждого из произв.: 1,7•1,4......... =2,38 1,73 • 1,41.......=2,4393 1,732•1,114......=2,449048   1,7320 • 1,1142...=2,44939440

и меньше каждого из произв.: 1,8•1,5..........=2,70 1,74 • 1,42.......=2,4708 1,733•1,415......=2,452195 1,7321 • .1,4143 ...=2,44970903

т. е. перемножить числа α и β — значит найти такое третье число, которое было бы больше произведения их любых приближенных значений, взятых с недостатком, но меньше произведения их любых приближенных значений, взятых с избытком.

в)  Возвысить   иррациональное   число   α   во  вторую, третью, четвертую и т. д. степени — значит найти произведение, составленное из двух, трех, четырех и т. д. сомножителей, равных  α.

г)  Обратные   действия  определяются   для иррациональных чисел так же, как и для рациональных; так, вычесть из числа  α число β  значит найти такое число х, чтобы сумма β + х равнялась α, и т. п.

Если одно из чисел α или  β будет рациональное, то в указанных определениях прямых действий вместо приближенных значений такого числа можно брать точное число.

Произведение иррационального числа на нуль принимается, как и для чисел рациональных, равным нулю.

Действия над отрицательными иррациональными числам и производятся согласно правилам, данным для рациональных отрицательных чисел.

При более обстоятельном рассмотрении можно установить, что действия   над  иррациональными   числами   обладают   теми  же свойствами, какие принадлежат действиям над числами рациональными; напр., сумма и произведение обладают свойствами переместительным и сочетательным; произведение и деление, кроме того, обладают еще распределительным свойством. Свойства, выражаемые неравенствами, также сохраняются у чисел иррациональных; так, если α >  β, то α + γ >  β,  αγ >  βγ (если γ > 0) и αγ <  βγ (если γ < 0) и т. п.

Действительные числа (R), их представление в виде десятичных дробей.

Еще древние греки обнаружили, что не всегда длину точно заданного отрезка можно выразить с помощью рационального числа. Например, если задан квадрат, длины сторон которого имеют длину, заданную рациональным числом, то какова длина его диагонали? Диагональ можно нарисовать точно, но невозможно выразить ее длину с помощью рационального числа. Такие отрезки называли несоизмеримыми. Однако, греками была разработана теория отношения отрезков, учитывая, что они могут быть несоизмеримы. Современная математика использует в этом случае понятие иррационального числа. Иррациональное число – число, которое не может быть представлено ни в виде дроби с целым числителем и знаменателем, ни в виде бесконечной периодичной десятичной дроби. Иррациональные числа могут быть представлены только бесконечными непериодическими дробями. Примеры иррациональных чисел: - это иррациональное число. = 1, 41… е = 2,718281828459045… Действительное числа, вещественное число – это любое рациональное или иррациональное число. Примеры действительных чисел: 3/5; 1,8; 7,121212…; ….

Изображение чисел на прямой. Модуль действительного числа, его геометрический смысл.

Числовая прямая, числовая ось, - это прямая на которой изображаются действительные числа. На прямой выбирают начало отсчета – точку О (точка О изображает 0) и точку L, изображающую единицу. Точка L обычно стоит справа от точки О. Отрезок ОL называют единичным отрезком. Точки, стоящие справа от точки О изображают положительные числа. Точки стоящие слева от точки. О, изображают отрицательные числа. Если точка Х изображает положительное число х, то расстояние ОХ = х. Если точка Х изображает отрицательное число х, то расстояние ОХ = - х. Число, показывающее положение точки на прямой, называется координатой этой точки. 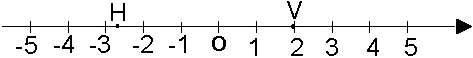    Точка V  изображенная на рисунке имеет координату 2, а точка H имеет координату -2,6. Модулем действительного числа называется расстояние от начала отсчета до точки, соответствующей этому числу.  Обозначают модуль числа х, так: | х |. Очевидно, что | 0 | = 0. Если число х больше 0, то | х | = х, а если х меньше 0, то | х | = - х. На этих свойствах модуля, основано решение многих уравнений и неравенств с модулем. Пример: Решить уравнение | х – 3 | = 1. Решение: Рассмотрим два случая – первый случай, когда х -3 > 0, и второй случай, когда х - 3  0. 1. х - 3 > 0, х > 3. В этом случае | х – 3 | = х – 3. Уравнение принимает вид х – 3 = 1, х = 4. 4 > 3 – удовлетворят первому условию. 2. х -30, х 3. В этом случае | х – 3 | = - х + 3 Уравнение принимает вид х + 3 = 1, х = - 2. -2 3 – удовлетворят второму условию.  Ответ: х = 4, х = -2.

Числовые выражения.

Числовое выражение – это совокупность одного или нескольких чисел и функций, соединенных знаками арифметических операций и скобками. Примеры числовых выражений: 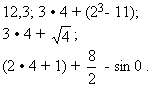Значением числового выражения является число. Операции в числовом выражении выполняются в следующей последовательности: 1. Действия в скобках. 2. Вычисление функций. 3. Возведение в степень 4. Умножение и деление. 5. Сложение и вычитание. 6. Однотипные операции выполняются слева на право. Так значением первого выражения будет само число 12,3 Для того чтобы вычислить значение второго выражения, действия будем выполнять в следующей последовательности: 1. Выполним действия в скобках  в следующей последовательности - сначала 2 возведем в третью степень, затем от полученного числа отнимем 11: 3 • 4 + (23 - 11) = 3 • 4 + (8 - 11) = 3 • 4 + (-3) 2. Умножим 3 на 4: 3 • 4 + (-3) = 12 + (-3) 3. Выполним последовательно операции слева направо: 12 + (-3) = 9. Выражение с переменными – это совокупность одного или нескольких чисел, переменных и функций, соединенных знаками арифметических операций и скобками. Значения выражений с переменными зависят от значений, входящих в него переменных. Последовательность выполнения операций здесь та же, что и для числовых выражений. Выражения с переменными иногда бывает полезно упрощать, выполняя различные действия – вынесение за скобки, раскрытие скобок, группировки, сокращение дробей, приведение подобных и т.д. Так же для упрощения выражений часто используют различные формулы, например, формулы сокращенного умножения, свойства различных функций и т. д.

Алгебраические выражения.

Алгебраическим выражением называется одна или несколько алгебраических величин (чисел и букв), соединенных между собой знаками алгебраических действий: сложения, вычитания, умножения и деления, а также извлечения корня и возведения в целую степень (причём показатели корня и степени должны обязательно быть целыми числами) и знаками последовательности этих действий (обычно скобками различного вида). Количество величин, входящих в алгебраическое выражение должно быть конечным. ^[1]

Пример алгебраического выражения:

«Алгебраическое выражение» — понятие синтаксическое, то есть нечто является алгебраическим выражением тогда и только тогда, когда подчиняется некоторым грамматическим правилам (см. Формальная грамматика). Если же буквы в алгебраическом выражении считать переменными, то алгебраическое выражение обретает смысл алгебраической функции.

Равенства и неравенства алгебраических выражений. Многочлены.

Алгебраические дроби. Формулы сокращенного умножения.

Степень с натуральным и рациональным показателем. Арифметический корень.