11.2. Прямолінійні твірні гіперболічного параболоїда

Розглянемо гіперболічний параболоїд, заданий канонічним рівнянням

(27)

Перетворимо це рівняння так:

Розглянемо дві системи рівнянь:

і

Ці системи визначають рівняння прямих, які повністю лежать на гіперболічному параболоїді, бо якщо перемножити відповідні части­ни рівнянь однієї системи, то одержимо рівняння (27) при довіль­ному Я, відмінному від нуля.

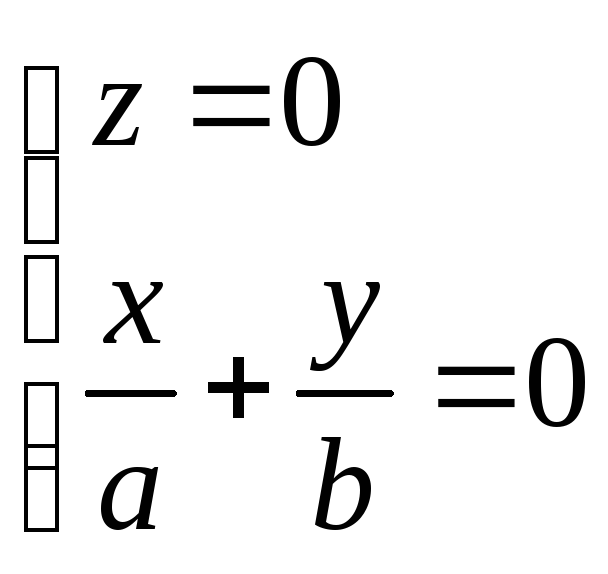
Аналогічно, як і для однопорожнинного гіперболоїда, крім запи­саних, є ще дві прямі, які також повністю належать гіперболічному праболоїду. Це такі прямі:

і

Всі ці прямі називаються прямолінійними твірни­ми гіперболічного параболоїда. Вони мають такі ж вла­стивості, як і прямолінійні твірні однопорожнинно­го гіперболоїда:

1. Рис. 31

   Через довільну точку гіперболічного параболоїда проходить одна і тільки одна твірна з кожної сім'ї.

2. Будь-які дві твірні однієї сім'ї є мимобіжними.

3. Будь-які дві твірні різних сімей перетинаються або паралельні.

Пропонуємо довести ці властивості самостійно. Таким чином, гіперболічний параболоїд також є лі­нійчатою поверхнею (рис. 31).

Можна показати, що однопорожнинний гіперболо­ їд утворюється рухом прямої, яка ковзає по трьох мимобіжних пря- мих. Аналогічно гіперболічний параболоїд можна утворити рухом прямої, яка ковзає по двох мимобіжних прямих і залишається при ньому весь час паралельною заданій площині. Природно виникає запитання: чи мають прямолінійні твірні такі поверхні другого порядку, як еліпсоїд, двопорожнинний гіперболоїд і еліптичний параболоїд? Відповідь проста: ні. Покажемо це на прикладі еліпсоїда. Як було встановлено в § 6, еліпсоїд лежить всередині деякого прямокутного паралелепіпеда, тобто є обмеженою поверхнею. Але кожна пряма є необмеженою лінією, а тому не може повністю лежати на еліпсоїді.

Приклад. На гіперболічному параболоїді знайти прямолінійні твірні, паралельні до площини 3x+2y-4z. Розв'язання. Запишемо рівняння двох сімей прямолінійних твірних даного гіперболічного параболоїда:

(36)

(37)

Знайдемо координати напрямних векторів прямих із сім'ї (36):

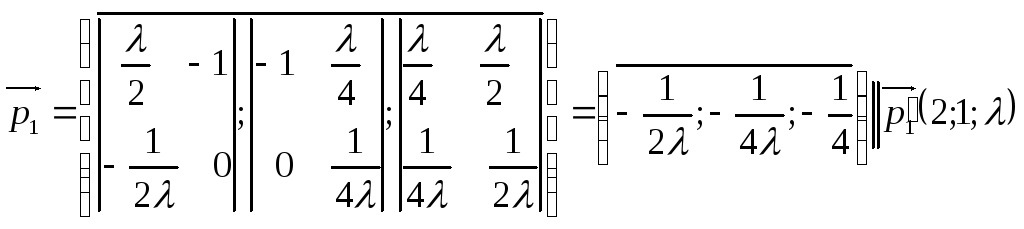
Координати напрямних векторів прямих (37):

Вектор паралельний до площини Зх + 2у — 4z = 0,

якщо 2 • 3 + 1 • 2 + λ• (-4) - 0, звідки λ = 2. Тоді прямою із сім'ї (36), паралельною до даної площини, є пряма

з напрямним вектором

Точка М1(4; -2; 0) належить цій прямій. Тому її канонічне рів­няня

Вектор паралельний до даної площини, якщо 2 • 3 -1 • 2+λ · (-4)=0, звідки λ= 1. Тому . Рівняння другої прямої:

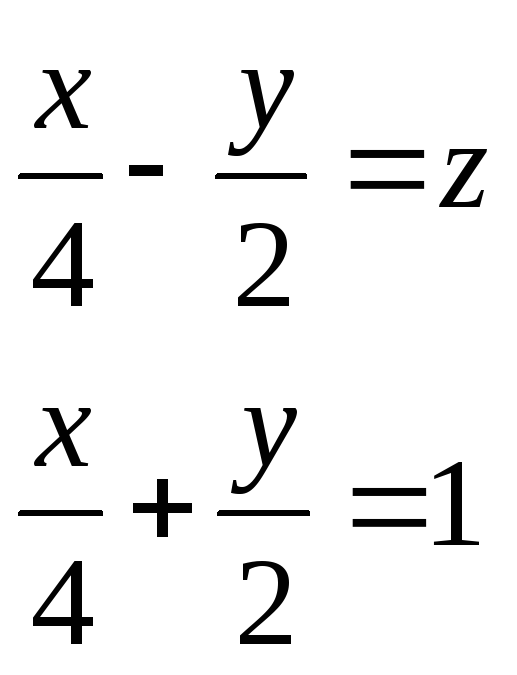
Цій прямій належить точка М₂(2; 1; 0), тому її канонічне рівняння

Відповідь. і

§ 12. Діаметральні площини поверхні другого порядку

Означення 12.1. Відрізок, який сполучає дві довільні точки поверхні другого порядку, називається хордою цієї поверхні.

Теорема 7.4. Середини паралельних хорд поверхні другого по­рядку лежать на площині.

Доведення. Нехай поверхня другого порядку задана загальним рівнянням у деякій системі координат OXYZ:

a₁₁х² + а.₂₂у² + а.₃₃z² + 2а₁₂ху + 2a_l3xz+

+ 2а₂₃уz + 2а₁₄х + 2а₂₄у + 2а₃₄z + а₄₄ = 0. (2)

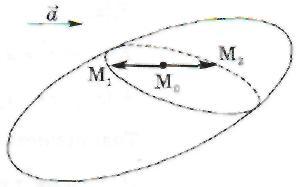
Розглянемо хорди цієї поверхні, паралельні до заданого вектора (рис. 32). Нехай М₁М₂ - одна з таких хорд, точка M₀(x₀ ;y₀ ; z₀) - її середина, координати кінців хорди: M₁(x₁ ;y₁ ; z₁) і М₃{х₃ ;у₃ ; z₃). Розглянемо вектори М₀М₁(х₁ -х₀; у₁ -у₀; z₁, -z₀) і

M_QM₂(x₂ - х₀; у₂ - y_Q; z₂ -z_Q). Ці вектори колінеарні з вектором а(і; т;n), причому один з них співнапрямлений з вектором а, а другий — протилежно напрямлений з а. Довжини цих векторів рівні. Тому

М₀М₁ - ta,

M₀M₂ = -ta, де t - деяке число, відмінне від нуля. Тоді

Рис. 32

звідки

(38)

(39)

Точки М₁ і М₂ лежать на даній поверхні, тому їх координати задовольняють рівняння (2). Підставивши (38) в (2), матимемо:

a₁₁ (x₀ +lt)² + a₂₂ (y₀ + mt) ²+ a₃₃ (z₀ +nt)² +2а₁₂(х₀ +lt)( x₀ +mt)+

+2а₁₃(x₀ +lt)(z₀ + nt) + 2а₂₃(y₀ +mt)(z₀ + nt) +2а₁₄(x₀ +lt)+ 2а₂₄, (y₀ + mt) + 2а₃₄ (z₀ + nt) + а₁₄ =0.

Беручи до уваги що , дістанемо

(a₁₁ l² + а₂₂т² + а₃₃ n² + 2a₁₂ lm+ 2a_l3 ln+ 2a₂₃ mn)t² +

+ 2((а₁₁х₀ + а₁₂у₀ + а₁₃z₀ + а₁₄ )l + (а₂₁х₀ + а₃₂у₀ + а₂₃z₀ + а₂₄)т +

+( a₃₁ x₀ + а₃₂у₀ + а₃₃z₀ + а₃₄ )nt+ a₁₁ x²₀ + а₂₂у²₀ + а₃₃z²₀ +

+2а₁₂x₀y₀ +2a₁₃x₀z₀+2a₂₃y₀z₀ +2a₁₄x₀ + 2а₂₄y₀ + 2а₃₄z₀ + а₄₄ = 0. (40)

Введемо позначення:

F(x;y;z)=+ а₁₁х²+ а₂₂у²+ а₃₃z²+2а₁₂xy+ 2а₁₃xz + 2а₂₃уz + 2а₁₄х + 2а₂₄y + 2а₃₄z + а₄₄;

F₁ (х; у; z) = а₁₁х + а₁₂у + а₁₃z + а₁₄;

F₂(x; .у; z)= а₂₁x + а₂₂у + a₂₃z + а₂₄;

F₃(x; y; z)= а₃₁х + а₃₂у + a₃₃z + а₃₄.

Тоді рівність (40) запишеться так:

(а₁₁l² + а₂₂т² +а₃₃п² + 2a₁₂lm + 2a₁₃ln+2a₂₃._imn)t²+2(lF_l(x_Q; y₀; z₀) +

+ mF₂(x₀; y₀; z₀)+ nF₃ (х₀; у₀; z₀))t + F(x₀; y₀; z₀) = 0. (41)

Аналогічно, підставивши (39) в (2), матимемо:

(а₁₁l²+ а₂₂m²+ а₃₃п²+ 2а₁₂lт +2а₁₃1п +2а₃₃тп)t²- 2(lF₁(x:₀; у₀;z₀)+

+ mF₂(x₀; у₀; z₀) + nF₃(х₀.; y₀; z₀))t + F(x₀; у₀; z₀) = 0. (42)

Віднявши відповідні частини (41) і (42), дістанемо:

4(lF₁(х₀; y₀; z₀)+ mF₂(x₀; у₀; z₀) + nF₃(х₀.; y₀; z₀))t

звідки випливає, що координати точки M_Q(x₀;y₀; z₀) задовольняють рівняння

lF₁(х₀; y₀; z₀)+ mF₂(x₀; у₀; z₀) + nF₃(х₀.; y₀; z₀)= 0. (43)

А це є рівняння першого порядку відносно x₀ ;у₀; z₀, тобто рівняння площини.

Теорему доведено.

Означення 12.2. Площина, яка проходить через середини хорд поверхні другого порядку, паралельних до деякого вектора 3, на­зивається діаметральною площиною цієї поверхні, спряженою з вектором а.

Як випливає з наведених вище міркувань, рівняння діаметраль­ної площини, спряженої з вектором а(l; т; п), має вигляд:

lF₁ +mF₂ +nF₃ =0. (44)

Приклад. Скласти рівняння діаметральної площини поверхні

х²- 4у² +z²-2x+ + 6y- 4xy + 2yz - 8 = 0_f спряженої з вектором а(1; - 2; 3).

Розв'язання. Для даної поверхні

F₁ = х - 2у - 1, F₂ -2х - 4у + z + 3, F₃ =y + z.

Із рівняння (44) маємо:

1· (x – 2y - 1)-2(- 2x – 4y + z + 3)+ 3(y + z)=0;

5х + 9y + z - 7 = 0.

Відповідь. 5х + 9у + z - 7 = 0.