Добавил:

ota Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Тольяттинский государственный университет

Предмет:

Геометрия

Файл:

геометрия модуль 4

.pdf

Скачиваний:

Добавлен:

26.07.2016

Размер:

409.33 Кб

Скачать

☆

1 / 41 2 3 4 > Следующая >>>

Ì4-3

Содержание Модуля ¹ 4

1. Метрические задачи (две основные метрические задачи)........................		-1
2.	Взаимная перпендикулярность двух прямых общего положения........	-4
3. Взаимная перпендикулярность двух плоскостей общего
	положения....................................................................................................................................	-5
4.	Построение плоскости, касательной к поверхности.................................	-6
5. Задачи на определение расстояний между геометрическими
	фигурами.....................................................................................................................................	-8
6.	Преобразование комплексного чертежа.............................................................	-10
7.	Способ замены плоскостей проекций....................................................................	-11
8.	Способ вращения вокруг проецирующей оси...................................................	-17
9.	Контрольные вопросы. Ответы на тесты ¹1, 2 .......................................	-29
10. Тест ¹1, 2 (метричские задачи).............................................................................		-30

Ì4-4

МОДУЛЬ ¹4

МЕТРИЧЕСКИЕ ЗАДАЧИ. ПРЕОБРАЗОВАНИЕ КОМПЛЕКСНОГО

ЧЕРТЕЖА

Модуль ¹4 предполагает знакомство с задачами, связанными с различными измерениями: натуральных величин отрезков, углов, плоских фигур; расстояний между фигурами и т.д. Вы узнаете, как проще решать метрические и позиционные задачи, используя способы преобразования комплексного чертежа. Кроме того, используя знания, полученные в модулях 1 - 3, Вы научитесь решать сложные инженерные конструктивные задачи.

Метрические задачи

"Ведь между двух соседних точек Прямая - самый краткий путь, Иначе слишком много кочек Необходимо обогнуть."

Л.Н.Мартынов

Как Вы думаете?

1.Что является кратчайшим расстоянием от точки до прямой, до плоскости?

2.Что является кратчайшим расстоянием между скрещивающимися прямыми, между двумя

параллельными плоскостями?

3. На чертеже рис. 4-1 показан угол АВС. Присутствует ли на какой-нибудь плоскости проекций натуральная величина угла?

À2 Â2

Ñ2

Â1

Ñ1

À1 Ðèñ. 4-1

Метрическими называются такие задачи, в условии или решении которых присутствуют геометрические фигуры или понятия, связанные с численной характеристикой.

Наиболее часто встречаются метрические задачи: на взаимную перпендикулярность геометрических фигур, на определение натуральной величины заданных отрезка или угла, на построение натурального вида плоской фигуры и т. п.

Из всего многообразия метрических задач выделяются две основные:

1. Первая основная метрическая задача - на перпендикулярность прямой и плоскости.

М4-5 2. Вторая основная метрическая задача - на определение натуральной

длины отрезка. Эта задача решается методом прямоугольного треугольника, который рассматривался в первом модуле.

Рассмотрим подробнее первую основную метрическую задачу.

Взаимная перпендикулярность прямой и плоскости.

Из элементарной геометрии известно, что прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости.

Задача: Через точку К Σ построить прямую п, перпендикулярную плоскости Σ(а || b). Анализ решения задачи провед¸м на пространственном чертеже, рис. 4-2.

		ï		Чтобы провести прямую п Σ,			ï
		Σ		Чтобы провести прямую п Σ,			ï
à		Σ	b	нужно в этой плоскости взять	à		Σ
à				две пересекающиеся прямые (на	à
ð		ò		две пересекающиеся прямые (на	h		b
ð	Ê	ò		ðèñ. 4-2 ýòî ð ∩ т = К). Прямую	h	Ê	b
	Ê			ðèñ. 4-2 ýòî ð ∩ т = К). Прямую		Ê	f
				п нужно строить перпендикулярно
Ðèñ. 4-2				одновременно двум этим прямым.	Ðèñ. 4-3

Однако, если прямые р и т будут прямыми общего положения, то прямой угол к ним ни на одной плоскости проекций не спроецируется в натуральную величину. Согласно теореме о проецировании прямого угла (см. свойство 2 ортогонального проецирования, модуль ¹1) прямой угол спроецируется в натуральную величину на какую-нибудь плоскость проекций, если одна сторона прямого угла будет параллельной этой плоскости проекций. Поэтому, в качестве прямых р и т выгодно взять горизонталь h и фронталь f (рис. 4-3). Тогда прямой угол между п и h спроецируется в натуральную величину на П1 , а прямой угол между п и f - на П2.

2			Плоский черт¸ж: На рис. 4-4 плоскость Σ задана параллельными
à	b
	2
K2			прямыми а и b. Точка К(К2) принадлежит этой плоскости. Нужно
K2			построить п Σ, ï Ê.
			построить п Σ, ï Ê.
			Согласно привед¸нным выше рассуждениям, в плоскости необходимо
		b	взять горизонталь и фронталь, затем, перпендикулярно каждой из них
		b
		1	строить п. Построения начинаем с горизонтали (рис. 4-5).
			строить п. Построения начинаем с горизонтали (рис. 4-5).
	a		Через точку К2 проводим h2 линиям связи,	K2	à2	b2
	a		Через точку К2 проводим h2 линиям связи,
Ðèñ. 4-4	1		находим h1 , а на ней, с помощью линии связи,		h2
Ðèñ. 4-4			находим h1 , а на ней, с помощью линии связи,
			Ê1 . Òàê êàê ï h, òî ï1 h1 , поэтому проводим
			Ê1 . Òàê êàê ï h, òî ï1 h1 , поэтому проводим
			ï1 h1 через точку K1 .
Аналогично находим п2 (рис. 4-6). Через точку К1 проводим							b
f1 линиям связи, находим f2. Òàê êàê ï f, mo n2 f2, поэтому				K1	1		b
проводим п2 f2 через точку К2.					h		1
							1
						a
Полностью решение задачи представлено на рис. 4-7.					n1	a
Видимость прямой п не учитывалась.				Ðèñ. 4-5		1
Видимость прямой п не учитывалась.				Ðèñ. 4-5

à2

ï2

K1 f1

Ì4-6

Алгоритмическая запись решения:

1.h Σ, f Σ, h ∩ f = K.

2.n K n1 K1 , n2 K2.

3.n h n1 h1 ;

4.n f n2 f2.

à2

ï2		h2
	K2	h2
	K2
K1	h1	f1
		f1

Ðèñ. 4-6

Ðèñ. 4-7 n1

Итак, чтобы задать на комплексном чертеже прямую п, перпендикулярную данной плоскости Σ, достаточно построить п1 è ï2, расположив их в любом месте чертежа, чтобы п1 h1

n2 f2,

где h и f - горизонталь и фронталь плоскости, при условии, что h∩f.

Если плоскость Σ занимает проецирующее положение, то прямая,

перпендикулярная ей, является линией уровня (рис. 4-8, 4-9).

ï2

ï2 =h2

Чтобы лучше понять данное

Σ2=f2

утверждение, нужно вспомнить , какие

прямые являются линиями уровня в

Σ1= h1

проецирующих плоскостях. Для этого

ï1 =f1

посмотрите рис. 2-12 и 2-14 в модуле ¹ 2.

Ðèñ. 4-9

Ðèñ. 4-8

Åñëè Σ- фронтально проецирующая:

Åñëè Σ- горизонтально проецирующая:

Ï2 f2=Σ2, h

Ï2.

Ï1 h1 =Σ1 , f

Ï1

ï h n1 h1

n h n h ,

} п - горизонталь.

n f n1

n f n2 f2

} п - фронталь.

Обратная задача.

Чтобы задать на чертеже плоскость, перпендикулярную данной прямой п, достаточно задать проекции горизонтали и фронтали этой плоскости так, чтобы f2 n2, a h1 n1 .

При этом, очевидно, должно выполняться условие h∩f (ðèñ. 4-10).

Если прямая п является прямой уровня, то плоскость, перпендикулярная ей, занимает проецирующее положение (рис. 4-11, 4-12) и

n 1

Ðèñ. 4-10

Ì4-7

может быть задана своей главной проекцией Σ1 èëèΣ2.

ï2

Если прямая п - горизонталь (рис. 4-11),

Σ2

то плоскость Σ, перпендикулярная ей,

Σ1

является горизонтально проецирующей (Σ1 ).

Если прямая п - фронталь (рис. 4-12),

то плоскость Σ, перпендикулярная ей,

Ðèñ. 4-11

Ðèñ. 4-12

является фронтально проецирующей (Σ2).

Если прямая п занимает проецирующее положение, то плоскость,

перпендикулярная ей, является плоскостью уровня (рис. 4-13, 4-14).

Σ2

Прямая п - горизонтально проецирующая

ï2

(ðèñ. 4-13), Σ п - горизонтальная плоскость

уровня (Σ2).

ï1

Σ1

ï1

Прямая п - фронтально проецирующая

(ðèñ. 4-14), Σ п - фронтальная

Ðèñ. 4-14

Ðèñ. 4-13

плоскость уровня (Σ1 ).

Все остальные метрические задачи так или иначе сводятся к решению первой основной

метрической задачи. Рассмотрим некоторые из них.

Взаимная перпендикулярность двух прямых

общего положения

Ê2

Задача: Через точку К, взятую на прямой общего

положения т, провести прямую п, тоже общего

положения, перпендикулярную т (рис. 4-15).

Так как прямой угол между прямыми общего

положения искажается на обеих плоскостях

проекций, то решение задачи на построение

Ê1

взаимно перпендикулярных прямых приходится

Ê1

сводить к задаче на построение взаимно

Ðèñ. 4-15

перпендикулярных прямой и плоскости.

При этом используется известное положение, что две прямые

Ðèñ. 4-16

перпендикулярны в том, и только в том случае, если через каждую

из них можно провести плоскость, перпендикулярную к другой прямой.

Алгоритм решения: 1. Через точку К проводим плоскость Σ, перпендикулярную прямой

т. Плоскость зада¸м пересекающимися горизонталью и фронталью (рис. 4-16), прич¸м, h1

m1 ,

a f2 m2.

2. Так как плоскость Σ(h∩f) m, то в этой плоскости можно взять некоторую прямую общего положения п, проходящую через точку К (рис. 4-17). Она будет перпендикулярна т. Зада¸м п1 .

ï	f2	ò2
2	Ê2 2
h	Ê2 2
2		2
		Ð2
		12
ò	21	Ð1
1
f1		11
ï1	h Ê1	11
	h Ê1
	1
Ðèñ. 4-17

Ì4-8

3.Известно, что прямую определяют две точки. На п1 , кроме К1 , возьм¸м ещ¸ одну точку Р1 .

4.Находим п2 в плоскости Σ. Для этого проводим в этой

плоскости прямую 12 (11 -21 ). Точка Р1 принадлежит этой прямой, а, следовательно, плоскости Σ. Находим Р2 и проводим прямую п2.

Алгоритмическая запись решения:

1. Σ ò, Σ= h ∩ f = K; h m h1 m1 , h2 K2K1 ; f m f2 m2, f1 K2K1 ;

2.n = PK, n Σ, n1 = P1 K1 ;

P1 11 21 P1 Σ → P2 → n2.

3.n Σ n m.

Взаимная перпендикулярность двух плоскостей общего положения

Известно, что две плоскости взаимно перпендикулярны, если в одной из них лежит прямая, перпендикулярная другой плоскости. Таким образом, построение взаимно перпендикулярных плоскостей общего положения сводится к построению взаимно перпендикулярных прямой и

плоскости.	Â2		Задача: Через точку К, взятую вне плоскости Г(АВС) провести
	Â2		Задача: Через точку К, взятую вне плоскости Г(АВС) провести
			плоскостьΣ Ã (ðèñ. 4-18).
À2			Алгоритм: 1. Плоскость Σ (ðèñ. 4-19) çàäà¸ì
		Ñ2	Ê2 пересекающимися прямыми т ∩ п = К. Согласно
			Ê2 пересекающимися прямыми т ∩ п = К. Согласно
			вышесказанному, одна из них должна быть


À1			перпендикулярна плоскости Г. Пусть это будет п.
À1			2. В плоскости Г бер¸м горизонталь и фронталь.
			2. В плоскости Г бер¸м горизонталь и фронталь.

	Ñ1			Â2
	Ê1			f		2
Ðèñ. 4-18		À		f		n
Ðèñ. 4-18		À	h2	2		n
	Â	2	h2		Ê2
	1			Ñ2	Ê2	m
3. Через точку К1	проводим п1 h1 , а через К2			Ñ2		2
3. Через точку К1	проводим п1 h1 , а через К2
проводим п2 f2 , следовательно, п Г.		À1
4. Прямую т, проходящую через точку К, зада¸м		À1	f1	Ñ1
4. Прямую т, проходящую через точку К, зада¸м
произвольно. Таким образом, Σ(ï∩ò) Ã(ÀÂÑ).						1
				h		n
Алгоритмическая запись решения:				h
Алгоритмическая запись решения:				1
1. h Ã h2→h1 , f Ã f1 →f2;						Ê
2. Σ= ò ∩ ï = K, ï Ã ï1 h1 , n2 f2.				Â		1
2. Σ= ò ∩ ï = K, ï Ã ï1 h1 , n2 f2.				Â
3. Σ Ã.				1		m1
3. Σ Ã.				Ðèñ. 4-19		m1

Ì4-9 Построение плоскости, касательной к поверхности

Касательная плоскость - это множество всех касательных прямых, провед¸нных к данной кривой поверхности и проходящих через одну е¸ точку.

На чертеже плоскость, касательную к поверхности, можно задавать, например, двумя пересекающимися прямыми, каждая из которых является касательной к поверхности в данной точке. Но можно касательную плоскость задавать различными условиями, характер которых

зависит от вида поверхности.	t'	S
Например, к конусу касательную плоскость можно	t'	t	M
провести так, чтобы она проходила через точку М			M
провести так, чтобы она проходила через точку М
(рис. 4-20), расположенную вне поверхности конуса.
Прич¸м, такая задача имеет два решения, так как		K'
через данную точку можно провести две плоскости,		K'
через данную точку можно провести две плоскости,
касающиеся поверхности конуса по образующим			K
SK и SK', которые в то же время являются касательными,			Ðèñ. 4-20
			Ðèñ. 4-20
соответственно, t и t'.

Как вы думаете?

1.Сколько плоскостей, касательных к поверхности конуса, можно провести через его вершину без других дополнительных условий?

2.Существуют ли особые точки на поверхностях сферы или эллипсоида, или они состоят только из обыкновенных точек? Для ответа на этот вопрос Вам нужно посмотреть модуль

¹1, раздел "Касательная и нормаль к кривой", стр. Ì1-30.

3.Сколько касательных плоскостей можно провести к эллипсоиду через любую точку на его

поверхности?		Задача: Через точку М (М2) на сфере Г с центром в точке О
Ã2		Задача: Через точку М (М2) на сфере Г с центром в точке О
Ã2	Ì2	провести плоскость Σ, касательную к е¸ поверхности (рис. 4-21).
	Ì2	Так как любая прямая, принадлежащая				Ì
Î2		Так как любая прямая, принадлежащая				2 t
		касательной плоскости к сфере,		Ã2		2
		касательной плоскости к сфере,				R
		будет перпендикулярна к е¸ радиусу,				2
		будет перпендикулярна к е¸ радиусу,
		то задача сводится к построению			Î2
		плоскости, перпендикулярной прямой.			Î2
		плоскости, перпендикулярной прямой.
		Плоскость удобно задать двумя		Ã1
Î		пересекающимися прямыми, каждая		Ã1
1		из которых будет перпендикулярна				t
		из которых будет перпендикулярна				t
Ã						1
Ã		радиусу сферы.			Î1	R
1						1
Ðèñ. 4-21	Алгоритм: 1. Находим М1		по принадлежности
	Алгоритм: 1. Находим М1		по принадлежности			M1
	сфере (рис 4-22).					M1
	сфере (рис 4-22).
2. Проводим R1 è R2		из центра сферы О1 è Î2	к точкам М1 è Ì2 .		Ðèñ. 4-22

Ã2

Ã1

		Ì			Ì4-10
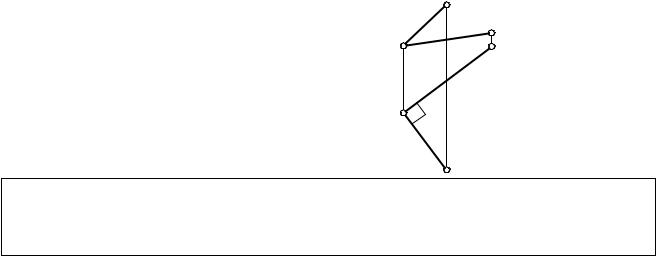
		Ì			3. Проводим t1 R1 - это горизонтальная проекция
		2	t		прямой, перпендикулярной радиусу, а, следовательно,
	R		2		касательной к сфере. Поскольку, прямой угол на П1
	R	2	t	'	касательной к сфере. Поскольку, прямой угол на П1
			2	'	спроецирован в натуральную величину, то прямая t -
			2
Î2
Î2					горизонталь, и е¸ проекция на П будет перпендикулярна
					2
					линиям связи →t2.
					4. Аналогично проводим построения второй касательной
			t		t', которая перпендикулярна радиусу (рис. 4-23): t2' R2,
			t
				1	t1 ' линиям связи, то есть t' - фронталь.
Î1		R			t1 ' линиям связи, то есть t' - фронталь.
		R	t1 '		5. Плоскость Σ(t∩t') R Σ - касательная к сфере.
		1

		M1			Примечание: В данной задаче видимость поверхности
Ðèñ. 4-23		M1			не учитывалась.
Ðèñ. 4-23

Алгоритмическая запись решения:

1.Ì Ã → Ì1 .

2.ÎÌ = R O1 M1 = R1 , O2M2 = R2.

3.Σ(t∩t') = M; t=h, t R t1 R1 , t2 M2M1 .

4.t'=f, t' R t2' R2, t1 ' M2M1 .

5.Σ R Σ- Ã.

Для решения этой задачи можно использовать другие рассуждения.

	à		Ì2	t2	1. Для нахождения точки М1	проводим параллель а (а2,à1 )
	à			t2	на поверхности сферы (рис. 4-24).
Ã2	2				на поверхности сферы (рис. 4-24).
Ã2					2. Проводим t - касательную к окружности а (а1 ,à2). t1 будет
	Î2				перпендикулярна радиусу сферы R1 , à t2, как касательная к
	Î2				à2, совпад¸т с а2.			Ì
					à2, совпад¸т с а2.			Ì
								2
Ã1					3. Проводим через точку
Ã1	à1				М касательную прямую к	Ã2	R 2	t
	à1			t	окружности с (с2,ñ1 )	Ã2		2 '
				1	окружности с (с2,ñ1 )		Î2
	Î1	R			(ðèñ. 4-25). t2', êàê		Î2
		1			(ðèñ. 4-25). t2', êàê		ñ2
					касательная к с2, будет		ñ2
			M1		касательная к с2, будет	Ã
			M1		перпендикулярна радиусу	Ã
	Ðèñ. 4-24				R2, à t1 ', как касательная	1
	Ðèñ. 4-24				R2, à t1 ', как касательная
					ê ñ1 , совпад¸т с с1 .		Î1	t1 '
4. Конечный результат этой задачи тот же, что и							Î1
4. Конечный результат этой задачи тот же, что и							ñ1
рассмотренный выше, и представлен на рис. 4-23.								M1
								M1

Ðèñ. 4-25

Ì4-11 Задачи на определение расстояний между

геометрическими фигурами К таким задачам относятся: задачи на определение расстояний от точки до прямой, до

плоскости, до поверхности; между параллельными и скрещивающимися прямыми; между параллельными плоскостями и т. п.

Все эти задачи объединяют три обстоятельства:

во-первых, поскольку кратчайшим расстоянием между такими фигурами является перпендикуляр, то все они сводятся к построению взаимно перпендикулярных прямой и плоскости.

во-вторых, в каждой из этих задач необходимо определять натуральную длину отрезка, то есть решать вторую основную метрическую задачу.

в-третьих, это сложные по составу задачи, они решаются в несколько этапов, и на каждом этапе решается отдельная, небольшая конкретная задача.

Рассмотрим решение одной из таких задач.

à 1

à2

Задача: Определить расстояние от точки М до прямой общего положения а (рис. 4-26).

Алгоритм: 1 этап: Расстояние от точки до прямой есть

Ì2	перпендикуляр. Поскольку прямая а - общего положения, то
	перпендикуляр. Поскольку прямая а - общего положения, то
	для построения перпендикуляра к ней необходимо решать
	задачу, аналогичную привед¸нной на стр. М4-4 данного
Ì1	модуля, то есть вначале через точку М провести плоскость
Ì1	Σ, перпендикулярную а. Зада¸м эту плоскость, как обычно,
	h ∩ f, ïðè ýòîì h1 a1 , a f2 a2 (ðèñ. 4-27).

Ðèñ. 4-26

22 b2

Ê2

Ê1

Ðèñ. 4-28 11

à2

f
2
h2
Ì2
1
h
f1
Ì1
à =	Ã
1	1

2 этап: Для построения перпендикуляра необходимо найти для него вторую точку. Это будет точка К, принадлежащая прямой а. Для е¸ нахождения нужно решить позиционную задачу, то есть, найти точку пересечения прямой а с плоскостью Σ. Решаем 1ГПЗ

по третьему алгоритму (рис. 4-28):


	- вводим плоскость - посредник Г,
	Ã	\|\|	Ï1 , Ã à Ã1 = à1 ;
	Ã		Ï1 , Ã à Ã1 = à1 ;
	- Ã ∩ Σ= b, Ã			\|\|	Ï1 b1 (11 21 ) = Ã1 ,
	- Ã ∩ Σ= b, Ã				Ï1 b1 (11 21 ) = Ã1 ,
= b	b Σ b2(1222) Σ2.
= b	- b2 ∩ a2 = K2 → K1 .
1	- b2 ∩ a2 = K2 → K1 .

à2

f 2

h2 Ì2

1	Ì
h	1

à 1

Ðèñ. 4-27

				Ì4-12
	à			3 этап: Находим натуральную
	2
Ê2	Í. âåë. ÌÊ			величину МК методом
Ê2		M		прямоугольного
		M
		}	y	треугольника (рис. 4-29).	h2
				треугольника (рис. 4-29).
	Ì2			Полное решение задачи
				Полное решение задачи
				показано на рис. 4-30.
				показано на рис. 4-30.
	Ì1		Алгоритмическая запись решения:
y {	Ì1		1. Σ à, Σ= h ∩ f = M
y {			h1 a1 , f2 a2.
Ê	à		h1 a1 , f2 a2.
Ê	à		2. Вводим плоскость - посредник Г,
1	1		2. Вводим плоскость - посредник Г,
Ðèñ. 4-29			- Ã \|\| Ï1 , Ã à Ã1 = à1 ;

-Ã ∩ Σ= b, Ã || Ï1 b1 (11 21 ) = Ã1 , b Σ b2(1222) Σ2.

-b2 ∩ a2 = K2 → K1 .

3.Находим натуральную величину МК.

Выводы:

22	b2	à2
	f
	2			Í. âåë. ÌÊ
	Ê2			Í. âåë. ÌÊ
	Ê2			M
			}
	12	Ì
		2
				h
		f1		1
21	{	f1	Ì1
	Ê1		à	=	Ã	= b
	11		à	=	Ã	= b
	11		1		1	1
				Ðèñ. 4-30

1.Решение всех метрических задач сводится к решению первой основной метрической задачи - на взаимную перпендикулярность прямой и плоскости.

2.При определении расстояний между геометрическими фигурами всегда используется вторая основная метрическая задача - на определение натуральной величины отрезка.

3.Плоскость, касательную к поверхности в одной точке, можно задать двумя пересекающимися прямыми, каждая из которых является касательной к данной поверхности.

Контрольные вопросы

1.Какие задачи называются метрическими?

2.Какие две основные метрические задачи Вы знаете?

3.Чем выгоднее задать плоскость, перпендикулярную прямой общего положения?

4.Как называется плоскость, перпендикулярная одной из линий уровня?

5.Как называется плоскость, перпендикулярная одной из проецирующих прямых?

6.Что называется плоскостью, касательной к поверхности?

1 / 41 2 3 4 > Следующая >>>

Соседние файлы в предмете Геометрия

#
26.07.20161.5 Mб23геометрия метод указания.pdf
#
26.07.2016711.97 Кб16геометрия модуль 2.pdf
#
26.07.2016402.34 Кб12геометрия модуль 3.pdf
#
26.07.2016409.33 Кб11геометрия модуль 4.pdf
#
26.07.2016576.48 Кб37геометрия раб тетрадь.pdf
#
26.07.2016556.58 Кб18геометрия.pdf