
- •2. Основные понятия математического моделирования
- •2. Принципы построения математических моделей
- •3.Классификационные признаки и классификация моделей
- •1.Основные этапы математического моделирования
- •2. Понятие о вычислительном эксперименте
- •3.Оценка свойств моделей
- •2.1. Метод нелинейного преобразования, обратного функции распределения
- •2.2. Метод суперпозиции
- •2.3. Некоторые специальные методы моделирования случайных величин
- •2.3.1. Метод Неймана
- •3.2. Метод кусочной аппроксимации
- •2.4. Моделирование векторных случайных величин
- •Раздел 2. Модели и методы исследования структурных свойств сетей связи
- •2. Изоморфность графов
- •1. Подграфы и дополнения
- •2. Деревья, разрезы, циклы
- •1. Матрица циклов и ее связь с матрицей инцидентности.
- •2.Матрица разрезов и ее связь с матрицей циклов
- •Матрицы смежности и перечисления путей
- •2. Связность
- •1. Степенная последовательность вершин графа
- •2. Алгоритм синтеза графов с максимальной связностью
- •3. Алгоритмы синтеза графов с максимальной связностью при заданном числе вершин и ребер.
- •4.Однородные графы. Мера неоднородности.
- •Модели и методы оценки разведзащищенности сетей связи
- •1.Показатели разведзащищенности сетей связи.
- •2.Модель оценки разведзащищенности сети связи.
- •Матрица смежности графа а
- •Матрица смежности графа в
- •Зависимость разведзащищённости от степени неоднородности сетей
- •5. Синтез сетей связи, оптимальных по показателям структурной устойчивости и разведзащищенности.
- •3.1. Моделирование марковских случайных процессов
- •3.2. Разностные и дифференциальные стохастические уравнения
- •2. Понятие эквивалентной функции стохастической сети
- •1.Метод двухмоментной аппроксимации.
- •3.Разложение на простые дроби.
- •3. Общие правила моделирования исследуемых процессов
2.3.1. Метод Неймана
Для моделирования СВ, возможные значения которых не выходят запределы некоторого ограниченного интервала (a, b), а также СВ, законраспределения которых можно аппроксимировать усеченными, достаточноуниверсальным является метод Неймана, состоящий в следующем.
С помощью датчика
равномерно распределённых в интервале
(0, 1) случайных чисел независимо выбираются
пары чисел
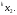 Из
нихформируются преобразованные пары
Из
нихформируются преобразованные пары
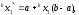
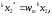
где (a,
b)
- интервал
возможных значений СВy
с заданной
ПРВ w(y);
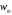 -максимальное
значение ПРВw(y).
В качестве
реализации СВ берется число
-максимальное
значение ПРВw(y).
В качестве
реализации СВ берется число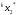 из
тех пар (
из
тех пар (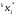
 ),
для которых выполняется неравенство
),
для которых выполняется неравенство
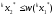 .
.
Пары, не удовлетворяющие
этому неравенству, отбрасываются.
Можнолегко убедиться в справедливости
такого метода моделирования
СВ.Действительно, пары случайных
чисел(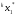
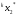 ),можно
рассматривать каккоординаты случайных
точек плоскости, равномерно распределенных
вдольосей y
и w(y)
внутри
прямоугольника aa'b'b(рис.
2).
),можно
рассматривать каккоординаты случайных
точек плоскости, равномерно распределенных
вдольосей y
и w(y)
внутри
прямоугольника aa'b'b(рис.
2).
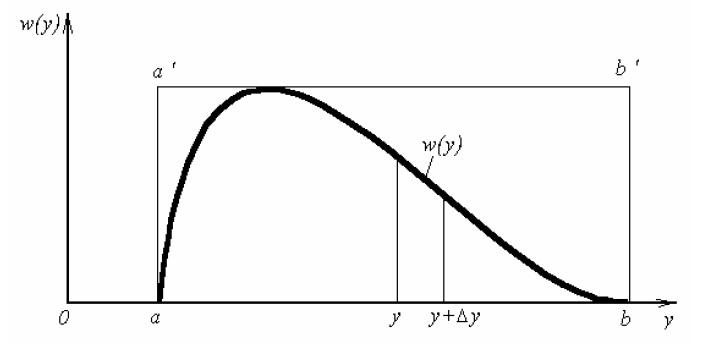
Рис. 2.2. Усеченная кривая плотности вероятности
Пары(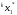
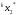 ),
удовлетворяющие условию неравенства,
представляютсобой координатыслучайных
точек плоскости, равномерно
распределенныхвдоль осей y
и w(
y)
внутри тойчасти
прямоугольника aa'b'b,
котораярасположена под кривой w(
y).
Вероятность
того, чтослучайная точкаплоскости,
находящаяся под кривой w(
y),
окажется в элементарной полосес
основанием (
y,
y +
Δy)
пропорциональна
w(
y),
а вероятность попаданияточки под кривую
w(
y)
по условию
равна единице, что и требуется.
),
удовлетворяющие условию неравенства,
представляютсобой координатыслучайных
точек плоскости, равномерно
распределенныхвдоль осей y
и w(
y)
внутри тойчасти
прямоугольника aa'b'b,
котораярасположена под кривой w(
y).
Вероятность
того, чтослучайная точкаплоскости,
находящаяся под кривой w(
y),
окажется в элементарной полосес
основанием (
y,
y +
Δy)
пропорциональна
w(
y),
а вероятность попаданияточки под кривую
w(
y)
по условию
равна единице, что и требуется.
3.2. Метод кусочной аппроксимации
Существуют различные приближенные приемы моделирования СВ:численноерешение уравнения x = F (y) относительно y при использованииметода нелинейного преобразования, обратного функции распределения;замена непрерывных распределений соответствующими дискретнымираспределениями, для которых можно указать достаточно простыемоделирующие алгоритмы и другие приёмы. Среди них универсальным инаиболее простым является метод кусочной аппроксимации.
Сущность этого метода состоит в следующем. Пусть требуется получитьСВy с функцией плотности w( y). Предположим, что область возможныхзначений СВy ограничена интервалом (a, b) (неограниченное распределениеможно приближенно заменить ограниченным). Разобьем интервал (a, b) на nдостаточно малых интервалов (am,am+1),
m=0,...,n−1,a0 =a,an=b, так, чтобы распределение заданной СВ в пределах этих интервалов можно былодовольно точно аппроксимировать каким-нибудь простым распределением(рис. 3), например, равномерным, трапецеидальным и т. д. В дальнейшем
рассмотрим кусочную аппроксимацию равномерным распределением.

Пусть Pm
- вероятность попадания СВy
в каждый из
интервалов (am,am+1).
Получатьреализации величины y
с
кусочно-равномерным распределением
можно, очевидно, в соответствии со
следующей схемой преобразования
случайных чисел: 1) случайным образом с
вероятностью Pmвыбирается
интервал (am,am+1);
2) формируется реализация
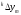 СВ,равномерно
распределенной в интервале
СВ,равномерно
распределенной в интервале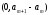 ;
3) искомаяреализация
;
3) искомаяреализация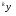 получается
по формуле
получается
по формуле
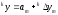
Случайный выбор
интервала (am,am+1)
с вероятностью
Pmозначает,
по существу, моделирование дискретной
СВ, принимающей n
значений
am,
m =
0, . . . , n
−1,
x0
=0,
xn
=,
с вероятностью Pmкаждое,
что можно сделать достаточно просто.
Интервал (0,
1) разбивается
на n интервалов
(xm,xm+1),
m =
0, . . . , n
−1,
x0
=0,
xn
=1,
длиной (xm+1−xm)=Pmкаждый.
Из датчика случайных, равномерно
распределенных в интервале (0,
1) чисел
выбирается некоторая реализация
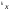 .
Путем последовательного сравнения
.
Путем последовательного сравнения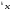 сxmопределяется
тот интервал (xm,xm+1),
в котором находится
сxmопределяется
тот интервал (xm,xm+1),
в котором находится
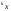 .
.
B основу этого процесса положен очевидный факт: вероятность попаданияравномерно распределенной в интервале (0, 1) СВ в некоторый подынтервал(xm,xm+1)равна длине этого подынтервала. Рассмотренный выше процесспредставляет интерес не только как составной элемент метода кусочнойаппроксимации, он широко используется в качестве алгоритма длямоделирования дискретных СВ и случайных событий.
Для моделирования СВ методом кусочной аппроксимации наиболее удобно при машиннойреализации выбирать вероятности попадания во все интервалы (am,am+1)одинаковыми Pm=1/n,ачислоnтаким,чтоn=2N,гдеN- целое число, меньше или равное количествудвоичных разрядов чисел,вырабатываемых датчиком случайных чисел. В этом случае величины amдолжны быть выбраны таким образом, чтобы выполнялось равенство
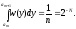
При равенстве вероятностей Pm для случайного выбора индекса m можноиспользовать первые N разрядов числа, извлекаемого из датчика равномернораспределенных случайных чисел.
Используя
рассмотренный прием, приходим к следующему
способупреобразования равномерно
распределенных случайных чисел в
случайныечисла с заданным законом
распределения. Из датчика
равномернораспределенных в интервале
(0,
1) случайных
чисел извлекается парареализаций
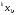
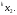 Первые
Первые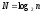 разрядов
числа
разрядов
числа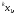 используются
длянахождения адресов ячеек, в которых
хранятся величиныam,am+1,
a затем поформуле
используются
длянахождения адресов ячеек, в которых
хранятся величиныam,am+1,
a затем поформуле
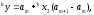 получается
реализация
получается
реализация СВy
с заданнымзаконом
распределения. Такой алгоритм является
довольно экономичным поколичеству
требуемых операций, которое не зависит
от числа n ,
т. е. не зависитот точностикусочной
аппроксимации. Однако с увеличением
точностиаппроксимации возрастает
количество ячеек памяти, требуемое для
хранениявеличин am,
m =
0,… , n
, что является
недостатком рассмотренного метода
прибольших значениях n
.
СВy
с заданнымзаконом
распределения. Такой алгоритм является
довольно экономичным поколичеству
требуемых операций, которое не зависит
от числа n ,
т. е. не зависитот точностикусочной
аппроксимации. Однако с увеличением
точностиаппроксимации возрастает
количество ячеек памяти, требуемое для
хранениявеличин am,
m =
0,… , n
, что является
недостатком рассмотренного метода
прибольших значениях n
.
