
- •Содержание
- •1. Функция. Основные определения. Последовательность. Предел последовательности
- •2. Предел функции непрерывного аргумента
- •3. Вычисление пределов функций. Основные приёмы
- •4. Замечательные пределы
- •5. Применение эквивалентных бесконечно малых к нахождению пределов функции. Сравнение бесконечно малых
- •6. Непрерывность функций. Точки разрывa.
- •Список литературы
- •Введение в математический анализ. Пределы
- •443086 Самара, Московское шоссе,34.
- •443086 Самара, Московское шоссе,34.
2. Предел функции непрерывного аргумента
Пусть
функция
 определена в некоторой окрестности
точки а или в некоторых точках этой
окрестности.
определена в некоторой окрестности
точки а или в некоторых точках этой
окрестности.
Определение.
Функция
 стремится к пределу
стремится к пределу (
( )
при х, стремящемся к
)
при х, стремящемся к (
( ),
если для каждого положительного числа
),
если для каждого положительного числа ,
как бы мало оно ни было, можно указать
такое положительное число
,
как бы мало оно ни было, можно указать
такое положительное число ,
что для всех х, отличных от а и
удовлетворяющих неравенству:
,
что для всех х, отличных от а и
удовлетворяющих неравенству: ,
имеет место неравенство
,
имеет место неравенство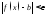


Рис. 3
Так
как из неравенства
 следует неравенство
следует неравенство ,
это значит, что на графике функции
,
это значит, что на графике функции ,
для всех точек х, отстоящих от точки а
не далее чем на
,
для всех точек х, отстоящих от точки а
не далее чем на ,
точки графика М лежат внутри полосы
шириной
,
точки графика М лежат внутри полосы
шириной ,
ограниченной прямыми
,
ограниченной прямыми и
и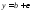 .
.
Если
 стремится к пределуb1
при х,
стремящемся к некоторому числу а так,
что х принимает только значения, меньшие
а, то пишут
стремится к пределуb1
при х,
стремящемся к некоторому числу а так,
что х принимает только значения, меньшие
а, то пишут
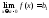 и называютb1
пределом функции
и называютb1
пределом функции
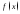 в точке слева.
в точке слева.

Рис. 4
Для
существования предела функции при
 не требуется, чтобы функция была
определена в точке х = а. При нахождении
предела рассматриваются значения
функции в окрест- ности а.
не требуется, чтобы функция была
определена в точке х = а. При нахождении
предела рассматриваются значения
функции в окрест- ности а.
Функция
 стремится к пределуb
при
стремится к пределуb
при
 ,
если для каждого произвольно малого
положительного числа
,
если для каждого произвольно малого
положительного числа можно указать такое положительное числоN,
что для всех х удовлетворяющих неравенству
можно указать такое положительное числоN,
что для всех х удовлетворяющих неравенству
 ,
будет выполняться
,
будет выполняться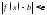


Рис. 5
Пример
1.
Докажем,
что
 .
Пусть задано произвольное
.
Пусть задано произвольное ,
для того чтобы выполнялось неравенство
,
для того чтобы выполнялось неравенство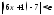 ,
необходимо выполнение неравенств
,
необходимо выполнение неравенств ;
;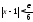 ;
; .
.
Таким
образом, при любом
 для всех значений х, удовлетворяющих
неравенству
для всех значений х, удовлетворяющих
неравенству ,
значение функции 6х+1 будет отличаться
от 7 меньше, чем на
,
значение функции 6х+1 будет отличаться
от 7 меньше, чем на .
А это значит, что 7 есть предел функции
при
.
А это значит, что 7 есть предел функции
при .
.
Пример
2.
Докажем, что


Нужно
доказать, что при произвольном
 будет выполняться неравенство
будет выполняться неравенство
 ,
если только
,
если только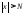 ,
причемN
определяется выбором
,
причемN
определяется выбором
 .
Данному неравенству эквивалентно
следующее:
.
Данному неравенству эквивалентно
следующее: ,
которое будет выполняться, если будет
,
которое будет выполняться, если будет .
Это и значит, что
.
Это и значит, что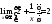 .
.
Функция
 стремится к бесконечности при
стремится к бесконечности при ,
т.е. является бесконечно большой величиной
при
,
т.е. является бесконечно большой величиной
при ,
если для каждого положительного числа
М, как бы велико оно ни было, можно найти
такое
,
если для каждого положительного числа
М, как бы велико оно ни было, можно найти
такое ,
что для всех значений х, отличных от а,
удовлетворяющих условию
,
что для всех значений х, отличных от а,
удовлетворяющих условию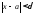 ,
имеет место неравенство
,
имеет место неравенство .
Тогда пишут:
.
Тогда пишут: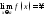 .
.
Если
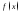 стремится к бесконечности при
стремится к бесконечности при и при этом принимает только положительные
или только отрицательные значения
соответственно пишут
и при этом принимает только положительные
или только отрицательные значения
соответственно пишут или
или .
.
Пример
3.
Докажем,
что

Возьмем
произвольное число M>0.
Если найдем такое число
 ,
что для всех х, удовлетворяющих
,
что для всех х, удовлетворяющих ,
где а=4, будет справедливо неравенство
,
где а=4, будет справедливо неравенство ,
где
,
где ,
то утверждение
,
то утверждение будет доказано.
будет доказано.
 ;
;
 ;
;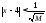 .
.
Если
положить
 и потребовать выполнения неравенства
и потребовать выполнения неравенства
 ,
то неравенство
,
то неравенство
 будет справедливо,
будет справедливо,
 .
.




Рис. 6
Геометрически
это означает, что для всех
 и
и соответствующие точки графика функции
соответствующие точки графика функции будут находиться выше прямой у = М, т.е.
будут находиться в бесконечной полуполосе,
ограниченной прямыми
будут находиться выше прямой у = М, т.е.
будут находиться в бесконечной полуполосе,
ограниченной прямыми и
и ,
у = М, причем у>М.
,
у = М, причем у>М.
Пример
4.
Докажем, что при
 функция
функция предела не имеет.
предела не имеет.
Функция
sinx
периодическая с периодом
 ,
следовательно, при неограниченном
возрастании аргумента эта функция
периодически пробегает все свои значения
,
следовательно, при неограниченном
возрастании аргумента эта функция
периодически пробегает все свои значения .
.
Но это значит, что при возрастании х значения функции не могут отличаться от любого постоянного числа все менее и менее. Значит функция sinx предела не имеет.
На
самом деле, из определения конечного
предела вытекает, что если функция имеет
конечный предел при
 то этот предел один. Следовательно, если
взять последовательность точек
то этот предел один. Следовательно, если
взять последовательность точек ,
то соответствующая последовательность
значений функции
,
то соответствующая последовательность
значений функции должна иметь предел, равный а.
должна иметь предел, равный а.
Возьмем
две последовательности
 .
.
1)
 ;
; ;
; ;
…;
;
…;
 ;
;
 ;
; ;
…;
;
…; ,
предел равен а=1.
,
предел равен а=1.
2)
 ;
; ;
; ;…;
;…;
 ;
;
 ;
; ;
…;
;
…; ,
предел равен а=0.
,
предел равен а=0.
Выделение
последовательности значений функции
sinx
при
 имеют различные пределы, следовательно,
данная функция предела не имеет.
имеют различные пределы, следовательно,
данная функция предела не имеет.
Задания для самостоятельной работы.
№1 Найти пределы функций или доказать, что они не существуют
а)
 ; б)
; б) ; в)
; в) ;
;
г)
 ; д)
; д) ; е)
; е)
№2
Доказать, что а)
 ;
б)
;
б)
№3
Доказать, что

№4
Доказать, что

