
- •Функция многих переменных: определение, геометрический смысл, область определения, область значений, линия уровня, поверхность уровня.
- •Частные приращения функции двух аргументов, частные производные первого порядка, частные производные высших порядков
- •Сложные функции и их дифференцирование.
- •Неявные функции и их дифференцирование.
- •Экстремум функции двух переменных, условный экстремум, наибольшее и наименьшее значение функции в замкнутой области.
- •Полное приращение и полный дифференциал функции двух аргументов первого порядка. Применение полного дифференциала к приближенным вычислениям.
- •Дифференциалы высших порядков от функции двух аргументов.
- •Касательная плоскость и нормаль к поверхности в заданной точке.
- •Скалярное поле, производная по направлению, градиент, их свойства.
- •Первообразная. Неопределенный интеграл: его свойства, геометрический смысл.
- •Интегрирование тригонометрических функций
- •Интегрирование дробно-рациональных функций.
- •Интегрирование некоторых трансцендентных функций.
- •Интегрирование простейших иррациональных алгебраических функций.
- •Интегрирование гиперболических функций
- •Интегральная сумма, определенный интеграл (определение, теорема существования, основные свойства, правила вычисления)
- •Геометрические приложения определенного интеграла: вычисление площади плоской фигуры, длины дуги плоской кривой, объема тела.
- •Физические приложения определенного интеграла: статические моменты и моменты инерции плоских дуг и фигур, нахождение координат центра тяжести, теоремы Гульдена, вычисление работы и давления
- •Несобственные интегралы: определение, признаки сравнения
- •Двойной интеграл: определение, геометрический смысл, свойства, правила вычисления, замена переменных
- •Геометрические приложения двойного интеграла: площадь плоской фигуры, объем тела, площадь поверхности
- •Физические приложения двойного интеграла: масса, статические моменты, координаты центра тяжести и моменты инерции пластины.
- •Тройной интеграл: определение, геометрический смысл, теорема существования, свойства, вычисление, теорема о среднем значении.
- •Приложения тройного интеграла: объем тела, масса, координаты центра тяжести, геометрические моменты инерции.
-
Сложные функции и их дифференцирование.
Пусть z=f(x,y).Если х и у – функции некоторой переменной t, т.е. x=φ(t), y=ψ(t)то z также является функцией от t. Предположим, что z ,x и y имеют непрерывные частные производные по всем своим аргументам. Найдем производную dz/dt.
Дадим аргументу t приращение ∆t, тогда х и y получат приращения ∆x и ∆y, а это значит, что z получит приращение ∆z.
![]() ,
где ρ-
бесконечно малая величина по сравнению
с ∆t,
т.е.
,
где ρ-
бесконечно малая величина по сравнению
с ∆t,
т.е. ![]() .
.
Разделим
все члены равенства на ∆t:
![]()
![]()
Пусть ∆t⇾0, тогда ∆x⇾0 и ∆y⇾0, а значит ε⇾0. Переходя к пределу при ∆t⇾0, получим
![]()
![]()
![]() Следовательно:
Следовательно:
![]() (8)
(8)
Рассмотрим
случай, когда z=f(x,y),
а x=φ(u,v),
y=ψ(u,v).
Тогда z будет
функцией от u и v.
Предполагая
существование непрерывных ![]() вычислим
вычислим![]() Дадим
аргументу u приращение ∆u,
сохраняя неизменным значение v. Тогда
задача сводится к уже рассмотренному
случаю. Значит, dz/dy существует
и согласно (8),
Дадим
аргументу u приращение ∆u,
сохраняя неизменным значение v. Тогда
задача сводится к уже рассмотренному
случаю. Значит, dz/dy существует
и согласно (8),
![]() (9).
Аналогично,
(9).
Аналогично, ![]() (10)
(10)
-
Неявные функции и их дифференцирование.
Неявная функция. Уравнение F(x,y,z)=0 в окрестностях точек (x0,y0,z0), для которых уравнение имеет хотя бы один корень z0, задает неявную функцию z=f(x,y), значения которой равны корням этого уравнения.
Если каждой паре чисел x, y из некоторой области соответствует одно или несколько значений z, которые удовлетворяют уравнению F(x,y,z)=0, то это уравнение неявно определяет одно или несколько значений однозначных функций z от x и y .
Пусть функция y=f(x) определяется уравнением F(x,y)=0
Подставим в F(x,y)=0 вместо y функцию f(x).Тогда F(x,y)=0 превратится в тождество относительно x. Продифференцируем данное тождество. Справа получим 0. Левая часть тождества - это сложная функция от x , обозначим её через z.
z=F(x,y), y=f(x).
По формуле (8) zx’=Fx’(x,y)xx’+Fy’(x,y)yx’.
Учитывая, что xx’=1, получим Fx’(x,y)+Fy’(x,y)yx’=0
Отсюда 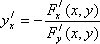 (12)
(12)
Рассмотрим уравнение вида F(x,y,z)=0
Найдём частные производные zx’ и zy’ неявной функции z от x и y. Прq1 `и вычислении zx’, y считаем постоянной величиной, поэтому, применив формулу (12), получим
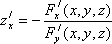 (14)
Аналогично,
(14)
Аналогично, 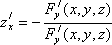 (15)
(15)
Таким же образом определяются неявные функции любого числа переменных и находятся их частные производные.
-
Экстремум функции двух переменных, условный экстремум, наибольшее и наименьшее значение функции в замкнутой области.
Говорят, что функция z=f(x,y) имеет максимум в точке M0(x0,y0), т.е. при x=x0, y=y0, если f(x0,y0)>f(x,y) для всех точек (x,y) , достаточно близких к точке (x0,y0) и отличных от неё. Говорят, что функция z=f(x,y) имеет минимум в точке M0(x0,y0) , т.е. при x=x0, y=y0, если f(x0,y0)<f(x,y) для всех точек (x,y) , достаточно близких к точке (x0,y0) и отличных от неё.
Максимум
и минимум функции называются экстремумами
функции.
Теорема (необходимое
условие экстремума функции двух
переменных). Если функция z=f(x,y) достигает
экстремума при x=x0,
y=y0,
то каждая частная производная первого
порядка от Z или
обращается в нуль при этих значениях
аргументов, или не существует.
Теорема (достаточное
условие экстремума функции двух
переменных). Пусть в некоторой области,
содержащей точку M0(x0,y0) функция z=f(x,y) имеет
непрерывные частные производные до
третьего порядка включительно. Пусть,
кроме того, точка M0(x0,y0) является
критической точкой функции f(x,y),
т.е.
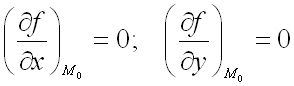 ,
тогда
при x=x0,
y=y0:
1) f(x,y) имеет
максимум, если дискриминант ∆=AC-B2>0 и A<0,
где
,
тогда
при x=x0,
y=y0:
1) f(x,y) имеет
максимум, если дискриминант ∆=AC-B2>0 и A<0,
где 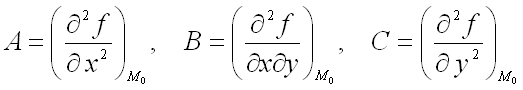 ;
2) f(x,y) имеет
минимум, если дискриминант ∆=AC-B2>0 и А>0;
3) f(x,y) не
имеет ни минимума, ни максимума, если
дискриминант ∆=AC-B2<0;
4)
если ∆=0 ,
то экстремум может быть, а может и не
быть (требуется дополнительное
исследование).
;
2) f(x,y) имеет
минимум, если дискриминант ∆=AC-B2>0 и А>0;
3) f(x,y) не
имеет ни минимума, ни максимума, если
дискриминант ∆=AC-B2<0;
4)
если ∆=0 ,
то экстремум может быть, а может и не
быть (требуется дополнительное
исследование).
Пусть функция z=f(x,y) определена и непрерывна в некоторой ограниченной замкнутой области D. Пусть в этой области заданная функция имеет конечные частные производные первого порядка (за исключением, быть может, конечного количества точек). Чтобы найти наибольшее и наименьшее значения функции двух переменных в данной замкнутой области требуется выполнить четыре шага простого алгоритма.
Алгоритм поиска наибольшего и наименьшего значений функции z=f(x,y) в замкнутой области D.
-
Найти критические точки функции z=f(x,y), принадлежащие области D.
Под критическими точками подразумевают такие точки, в которых обе частные производные первого порядка равны нулю (т.е. ∂z/∂x=0 и ∂z/∂y=0) или хотя бы одна частная производная не существует.
Часто точки, в которых частные производные первого порядка равны нулю, именуют стационарными точками. Таким образом, стационарные точки – есть подмножество критических точек.
-
Исследовать поведение функции z=f(x,y) на границе области D, найдя точки возможного наибольшего и наименьшего значений.
-
Найти значения функции z=f(x,y) во всех точках, полученных в предыдущих двух пунктах.
-
Из значений, полученных в третьем пункте, выбрать наибольшее и наименьшее.
Условным экстремумом функции z=f(x,y) в точкеM0(x0;y0) называется экстремум этой функции, достигнутый при условии, что переменные x и y в окрестности данной точки удовлетворяют уравнению связи φ(x,y)=0.
Если из уравнения связи можно выразить одну переменную через другую, то задача определения условного экстремума сводится к задаче на обычный экстремум функции одной переменной. Например, если из уравнения связи следует y=ψ(x), то подставив y=ψ(x) в z=f(x,y), получим функцию одной переменной z=f(x,ψ(x)).
Метод множителей Лагранжа состоит в том, что для отыскания условного экстремума составляют функцию Лагранжа: F(x,y)=f(x,y)+λφ(x,y) (параметр λ называют множителем Лагранжа). Необходимые условия экстремума задаются системой уравнений, из которой определяются стационарные точки:
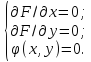
Достаточным условием, из которого можно выяснить характер экстремума, служит знак d2F=F′′xxdx2+2F′′xydxdy+F′′yydy2. Если в стационарной точке d2F>0, то функция z=f(x,y) имеет в данной точке условный минимум, если же d2F<0, то условный максимум.
