
- •Оглавление
- •1. ВВЕДЕНИЕ В ГИДРОМЕХАНИКУ
- •2. ЭЛЕМЕНТЫ ТЕНЗОРНОГО АНАЛИЗА
- •3. ГИДРОСТАТИКА
- •4. КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
- •5. ДИНАМИКА НЕВЯЗКОЙ ЖИДКОСТИ
- •6. ДИНАМИКА ВЯЗКОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ
- •6.1. Вязкость
- •МОДУЛЬ 2. ДВУХФАЗНЫЕ ПОТОКИ ЖИДКОСТИ И ГАЗА
- •7. ГАЗОВАЯ ДИНАМИКА
- •8. ВИЖЕНИЕ ВЯЗКОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ В ТРУБАХ
- •10. КАВИТАЦИЯ
- •ПРИЛОЖЕНИЕ 1
- •ПРИЛОЖЕНИЕ 2
- •ПРИЛОЖЕНИЕ 3
- •ПРИЛОЖЕНИЕ 4
- •ПРИЛОЖЕНИЕ 5
- •БИБЛИОГРАФИЧЕСКИЙ СПИСОК

4. КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
Кинематика – раздел механики капельных жидкостей, в котором рассматриваются виды и формы движения жидкости без выяснения природы и сил, вызывающих это движение. По образному выражению Н. Е. Жуковского, кинематика – это «геометрия движения». В кинематике используется свойство, общее для всякой сплошной среды, – непрерывность распределения параметров движения в пространстве и дифференцируемость их в пространстве и времени. Способы задания движения в кинематике жидкости (газов) отличаются от известных способов в кинематике отдельной материальной точки или системы точек. При движении свободного жидкого объема (в отличие от твердого тела) в его разных точках скорости частиц жидкости различны и объем деформируется. Движение жидкости будет определенным тогда, когда известны перемещения всех ее элементов.
4.1. Понятиеполяфизическойвеличины
Чтобы описать движение жидкости, необходимо задаться определенными свойствами ее в каждой точке (скоростью, давлением, плотностью и др.). Непрерывность распределения характеристик в сплошной среде приводит к понятию поля физической величины, под которым понимают часть пространства, в каждой точке которого физическая величина определена однозначно.
Если поле физической величины не зависит от времени, его называют стационарным, или установившимся. Поле физической величины нестационарно, если его параметры зависят от времени. Однако понятие стационарности (нестационарности) поля относительно.
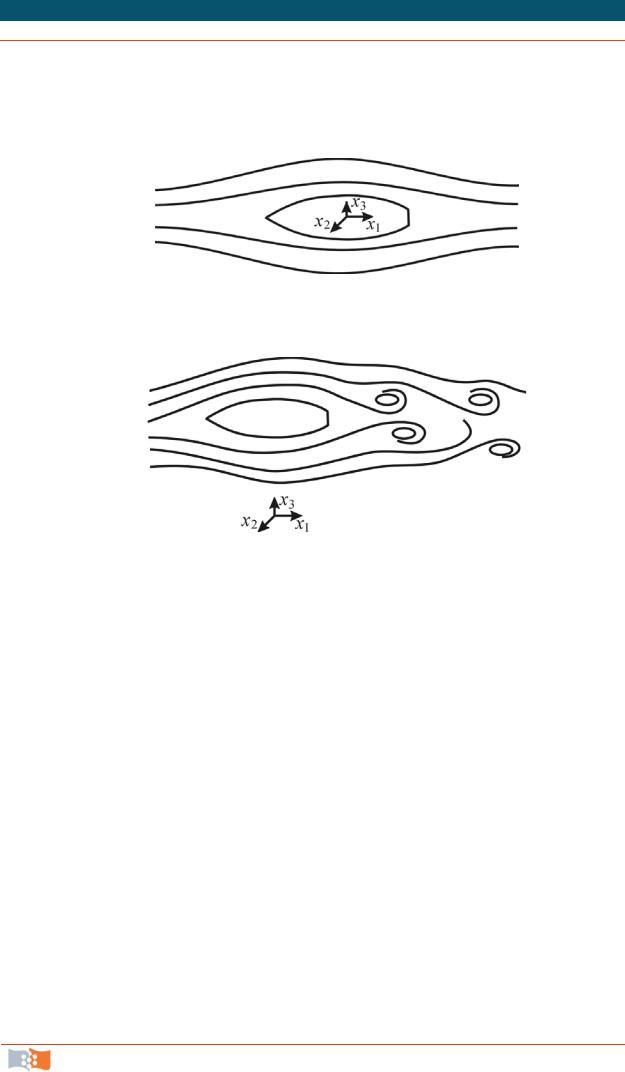
В зависимости от скорости и направления движения наблюдателя относительно исследуемой системы «жидкость – тело» картина одного и того же течения существенно изменяется. Если наблюдатель неподвижен по отношению к телу, например находится на корабле, движущемся поступательно, прямолинейно и равномерно, он видит картину линий тока относительного движения воды (рис. 4.1). Поле скоростей, возникающее при этом, стационарно, если движение относить к координатной системе, связанной с кораблем. Если же наблюдатель неподвижен относительно жидкости, например находится на берегу, то движущимся элементом в системе координат, связанной с берегом, становится и корабль, и вода. В этом случае наблюдатель видит картину линий тока абсолютного движения жидкости (рис. 4.2).
Линия тока – линия, в каждой точке которой в один и тот же момент времени вектор скорости частицы жидкости касателен к ней. При неизменных
Гидрогазодинамика. Учеб. пособие |
58 |
4.КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
4.1.Понятие поля физической величины
условиях обтекания твердого тела жидкостью абсолютные течения являются неустановившимися, а относительные установившимися, стационарными (их еще называют обращенными движениями). Следовательно, от выбора привязки системы координат зависит, каким будет представляться течение.
Рис. 4.1
Рис. 4.2
Поля могут быть скалярных, векторных и тензорных величин. Скалярное поле – поле скалярной величины, или множество
x1 , x2 , x3 , t .
Кскалярам в механике жидкости относятся плотность, давление, температура и др. Значения этих параметров в данной точке и при данных условиях не зависят от выбора системы координат, т. е. скалярные величины инвариантны относительно системы координат.
Сцелью наглядного представления о поле вводят понятие поверхностей уровня, т. е. таких геометрических мест (в данный момент времени), в которых физическая величина имеет одно и то же значение (изотермы, изобары, изопотенциальные поверхности и др.).
Уравнение поверхности уровня:
x1, x2 , x3 , t const C .
Гидрогазодинамика. Учеб. пособие |
59 |
4.КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
4.1.Понятие поля физической величины
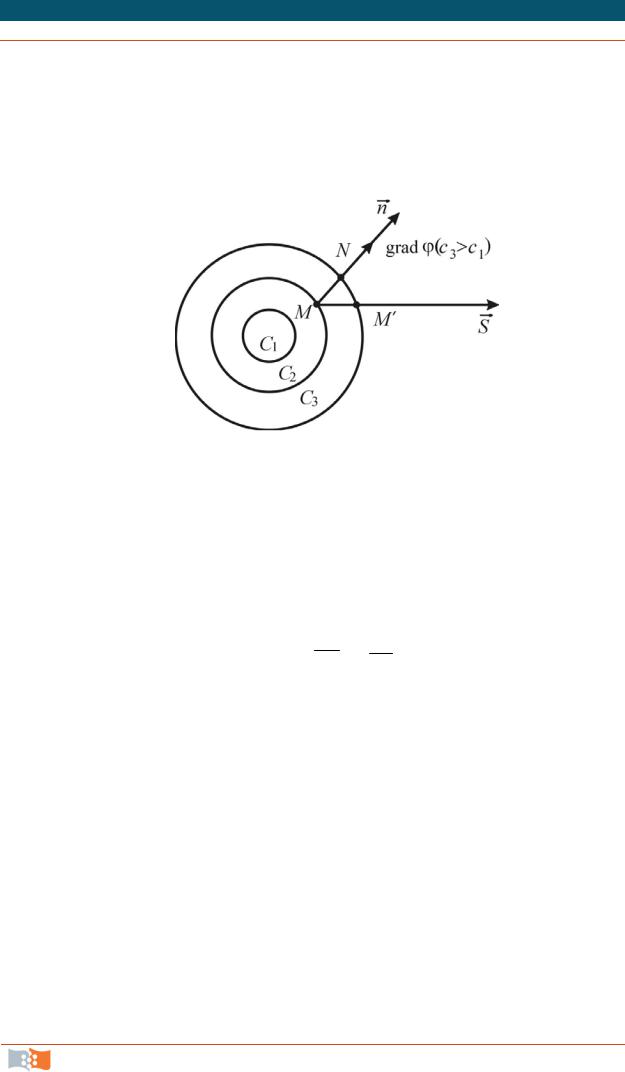
«Расслоив» мысленно пространство поверхностями уровня (рис. 4.3), упростим рассмотрение поля. Условимся называть внешним пространством по отношению к данной поверхности уровня ту область, где константа С имеет большее значение. Нормаль, направленная в сторону возрастания функции (рис. 4.3), является главной, или внешней, нормалью, направление которой принимается за положительное.
Рис. 4.3
Интенсивность поля скалярной величины (функции) определяется ее градиентом grad . Градиент функции есть вектор, направленный по внешней
нормали к поверхности уровня и равный по величине производной от этой функции по внешней нормали:
grad ddn n ; ddn 0 .
Следовательно, несмотря на то что скаляры определяются одним вещественным значением, изменение их в пространстве характеризуется векторно, т. е. фиксируется направление изменения физической величины. Градиент функции по внешней нормали, по определению производной, есть величина всегда положительная.
Кроме того, grad , взятый по направлению главной нормали (рис. 4.3), есть максимальное значение производной от функции. Например, возьмем
произвольное направление S в поле (рис. 4.3) и вычислим производную от
по этому направлению; т. к. |
MN MM |
|
(всегда), |
d |
|
d |
по определению |
|
dS |
dn |
производной.
С векторным полем связаны понятия линий и трубок тока. Проведем в данный момент времени замкнутый, себя не пересекающий контур. Через каждую точку этого контура можно провести линию тока. Совокупность ли-
Гидрогазодинамика. Учеб. пособие |
60 |
4.КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
4.1.Понятие поля физической величины
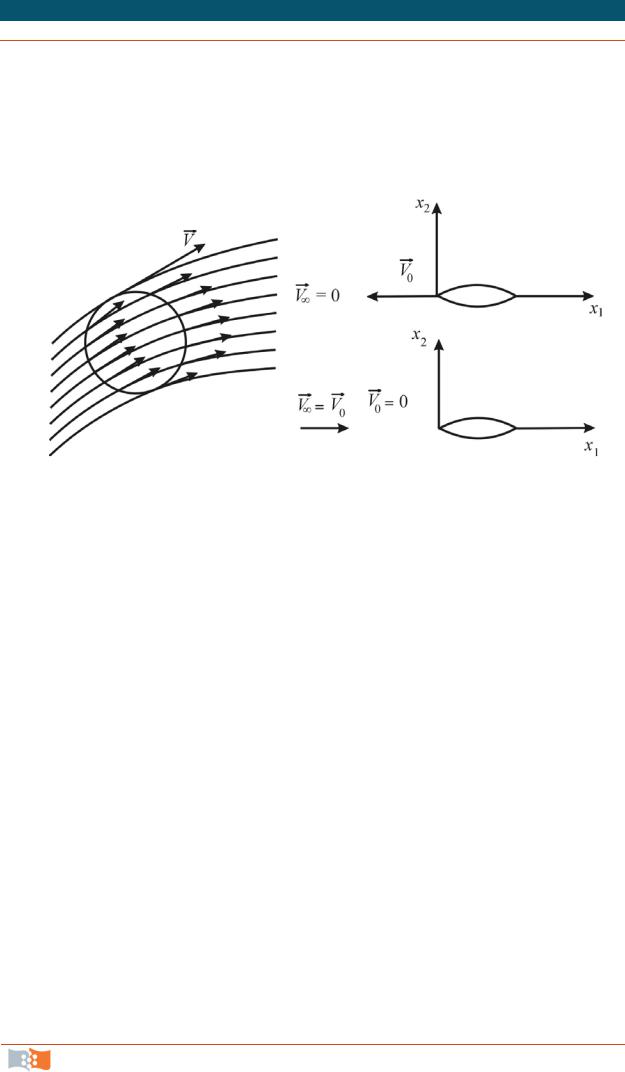
ний тока образует трубчатую поверхность – трубку тока, или векторную трубку (рис. 4.4).
В опытах по изучению движения тел в жидкости часто используют относительное (обращенное) движение, когда тело и связанная с ним система координат неподвижны. Набегающему потоку сообщают постоянные скорости, равные по величине и противоположные по направлению скорости тела.
Рис. 4.4 Рис. 4.5
К установкам, в которых используется принцип обращенного движения, относятся аэро- и гидродинамические трубы и гидролотки.
В кинематическом отношении движения абсолютное и обращенное не совпадают (см. рис. 4.5, где показаны скорости вблизи тела и далеко на бесконечности от него). Силы же, действующие в жидкости, одинаковы в обоих
случаях. Поскольку связь между скоростью абсолютного Vабс |
и |
||||||||||||||
Vобр обращенного движения можно представить в виде |
|
||||||||||||||
|
|
|
|
|
|
Vобр Vабс |
V0 , |
|
|||||||
для ускорений соответственно |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
dVобр |
|
|
dV |
|
dV |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
абс |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt . |
|
||
|
|
|
|
|
dt |
|
|
dt |
|
|
|||||
|
dV |
dVобр |
|
|
|
dV |
|
|
|
|
|
|
|||
Так как |
0 |
0 , то |
|
|
|
|
|
|
абс |
, что и доказывает предположение о |
|||||
dt |
dt |
|
|
|
dt |
|
|||||||||
равенстве сил в обоих случаях.
Течения жидкости могут быть также пространственными, плоскопараллельными и осесимметричными. Поле скоростей соответственно можно представить в следующем виде:
Гидрогазодинамика. Учеб. пособие |
61 |
4.КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
4.1.Понятие поля физической величины
V1,2,3 f x1, x2 , x3 для пространственного течения;
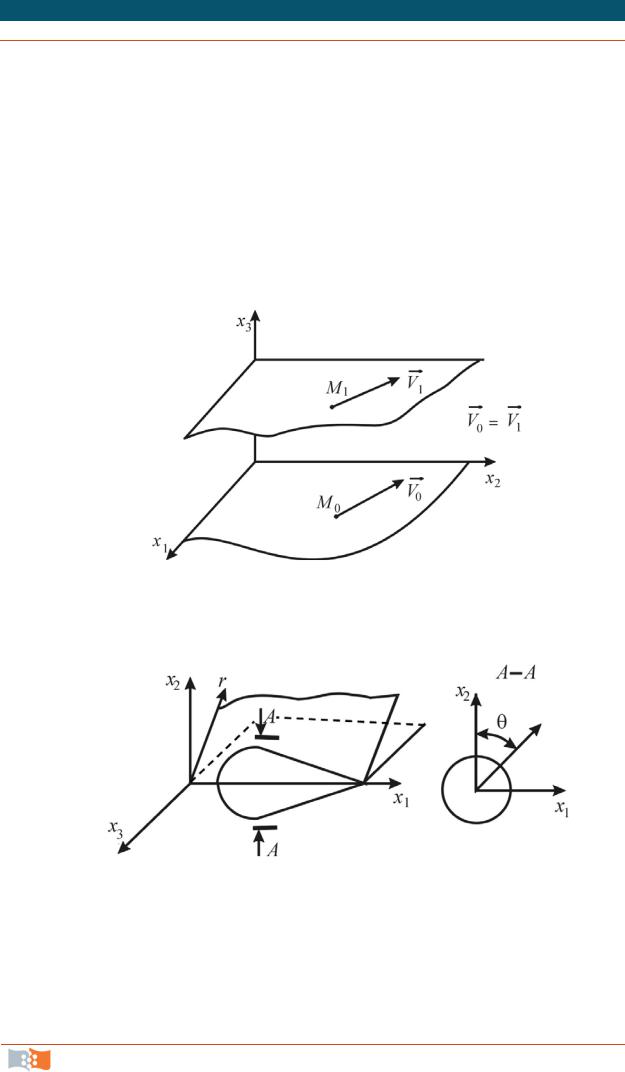
V1,2 f x1, x2 , V3 0 для плоскопараллельного течения, когда картина
течения в плоскостях, нормальных к некоторой оси (рис. 4.6), одинакова; V1,r f x, r, t , V0 0 в случае осесимметричного течения в цилиндри-
ческой системе координат, когда поле скоростей во всех плоскостях, проходящих через некоторую прямую (ось симметрии), одинаково (рис. 4.7).
В декартовой системе координат поле скоростей для осесимметричного случая определяется уже тремя пространственными координатами. Наибольшую сложность для изучения представляют пространственные течения как общий случай движения жидкой среды.
Рис. 4.6
Рис. 4.7
Трубка тока и струя это не одно и то же. Струя образована траекториями частиц движущейся жидкости. Трубка тока – совокупность линий тока.
Гидрогазодинамика. Учеб. пособие |
62 |
4.КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
4.1.Понятие поля физической величины
Ниже приведены примеры определения линий тока и траекторий по заданному полю скоростей.
Пример. Движение жидкости задано проекциями скоростей V1 ax2 , V2 ax1 , V3 0 , где а постоянная.
Исследуемое движение является плоским (V3 0 ) и установившимся, т. к. V1 и V2 от времени не зависят.
Запишем дифференциальные уравнения линий тока:
dx1 dx2 , V1 V2
или, подставляя значения V1 и V2 в последнее выражение, dx1 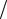 ax2 dx2
ax2 dx2 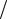 ax1 .
ax1 .
Разделив переменные, получим
x1dx1 x2dx2 0
и, интегрируя, найдем уравнение линий тока:
x12 x22 C ,
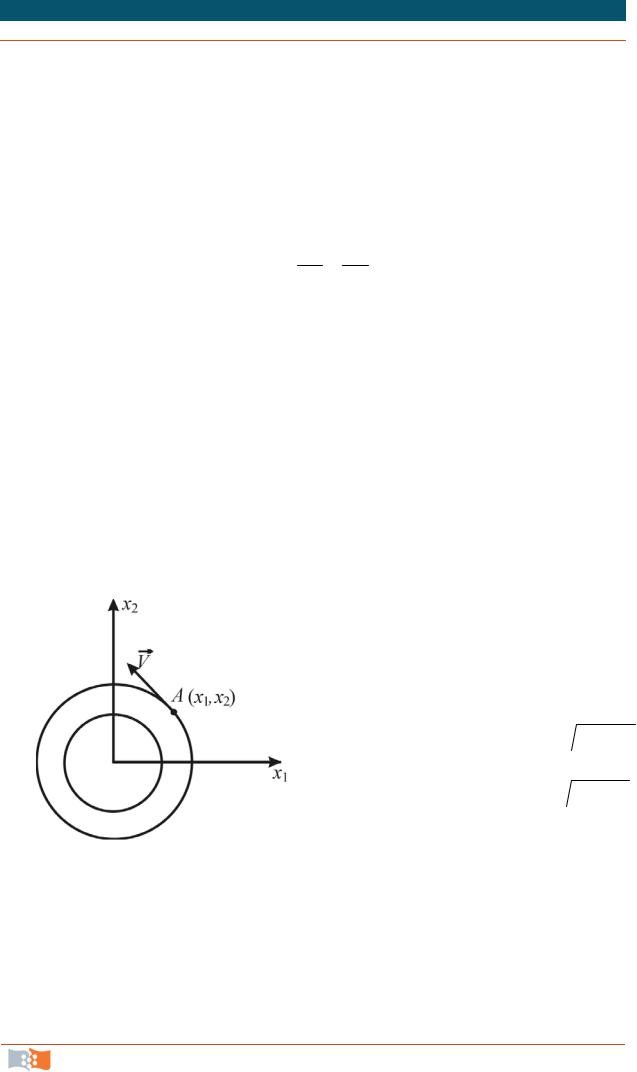
которое представляет собой семейство концентрических окружностей с центром в начале координат (рис. 4.8). Такое движение называется плоским вихрем. Траектории в данном случае совпадают с линиями тока. Направление движения жидкости определяется по косинусам углов между вектором
скорости и началом координат:
сos V x1 V1 /V x2 /  x12 x22
x12 x22
,
сos V x2 V2 /V x1 /  x12 x22
x12 x22
.
Рис. 4.8
Гидрогазодинамика. Учеб. пособие |
63 |

4.КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
4.2.Дваметодакинематическогоисследования теченияжидкости
Для глубокого и всестороннего исследования движения жидкости необходимо знать для каждого момента времени и каждой частицы жидкости ее местоположение в пространстве. В механике жидкости с этой целью используются два метода кинематики Лагранжа и Эйлера.
По методу Лагранжа изучается поведение отдельной частицы жидкости за время ее движения в пространстве. Пусть в начальный момент времени t0 выделенная жидкая частица характеризуется определенными тремя чис-
лами a, b, c, которые служат обозначением данной частицы жидкости при исследовании течения. Пусть в любой другой момент времени t координатами частицы в прямоугольной системе координат будут x1, x2, x3. Эти координаты являются функциями не только времени движения (начиная с t0 ), но и на-
чальных координат – тройки чисел a, b, c, обозначающих частицу, т. е.
x1 |
x1 a, b, c, t , |
|
|
x2 x2 |
|
|
|
a, b, c, t , |
(4.1) |
||
x |
x |
a, b, c, t . |
|
3 |
3 |
|
|
Уравнения (4.1) и числа a, b, c и t называются соответственно уравнениями и переменными Лагранжа. Уравнениями (4.1), по сути, задаются траектории движения отдельных частиц жидкости. Для полной характеристики состояния движущейся жидкости необходимо знать распределение давления P и плотность . Уравнения движения, составленные по методу Лагранжа,
обычно трудно разрешимы.
Метод, предложенный Эйлером, проще и нашел более широкое применение на практике. Этот метод не учитывает индивидуальных траекторий отдельных частиц. Здесь достаточно знать скорость жидкости в каждой точке пространства и ее направление, т. е. знать поле скоростей, которое в общем случае может изменяться в пространстве и во времени:
V1 |
V1 x1, x2, x3, t , |
|
||
|
|
|
|
|
V2 V2 x1, x2, x3, t , |
(4.2) |
|||
V |
V |
x , x , x , t . |
|
|
3 |
3 |
1 2 3 |
|
|
Совокупность величин x1, x2, x3, t называют переменными Эйлера; движение среды, по Эйлеру, задается полем скоростей.
Основное различие методов Лагранжа и Эйлера заключается в выборе системы отсчета: по Лагранжу, система a, b, c связана с жидкостью; по Эйлеру, x1, x2, x3 это некоторая система координат, относительно которой протекает жидкость. Оба метода равноправны.
Гидрогазодинамика. Учеб. пособие |
64 |

4.КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
4.3.Основныекинематические элементыдвиженияжидкости
Как уже отмечалось, линия тока – это геометрическая линия, проходящая через различные точки пространства в данный момент времени так, что векторы скоростей находящихся там частиц будут касательными к этой линии. Линии тока можно непосредственно наблюдать или сфотографировать, если ввести в поток какой-либо краситель или прикрепить к поверхности обтекаемого тела (крыла и т. п.) шелковинки.
Траектория частицы – это линия, определяющая положение частицы в разные моменты времени.
Линия тока отличается от траектории тем, что указывает направление скоростей разных частиц в один и тот же момент времени. Имеется лишь один, но весьма важный случай, когда линии тока совпадают с траекториями.
Это случай установившегося движения V V t const . Каждая частица в
этом случае движется по линии тока, т. к. в любой точке на своем пути она имеет скорость, которую имели все частицы, проходившие через эту точку в другие моменты времени.
Предположим, что поле (совокупность точек пространства, занятого потоком) скоростей известно и нужно найти линию тока. Из определения линии тока следует, что вектор скорости направлен к ней по касательной. Выделим на ли-
нии тока (рис. 4.9) элемент ду- Рис. 4.9 ги dS с проекциями на декар-
товы оси координат dx1, dx2, dx3. Так как вектор скорости V
и вектор dS параллельны, то векторное произведение их равно нулю:
dS V 0 . |
(4.3) |
Запишем это равенство с помощью определителя третьего порядка:
i |
j |
k |
|
|
|
|
|
||||
dx1 |
dx2 |
dx3 |
|
0. |
(4.4) |
V1 |
V2 |
V3 |
|
|
|
Гидрогазодинамика. Учеб. пособие |
65 |
4.КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
4.3.Основные кинематические элементы движения жидкости
Определитель равен нулю, если элементы двух его строк равны или пропорциональны, отсюда
dx |
dx |
|
dx |
|
V 1 |
V |
2 |
V 3 . |
(4.5) |
1 |
2 |
3 |
|
|
Полученная система представляет дифференциальные уравнения линий тока. Интегрируя ее, находят положение линий тока в данный момент времени.
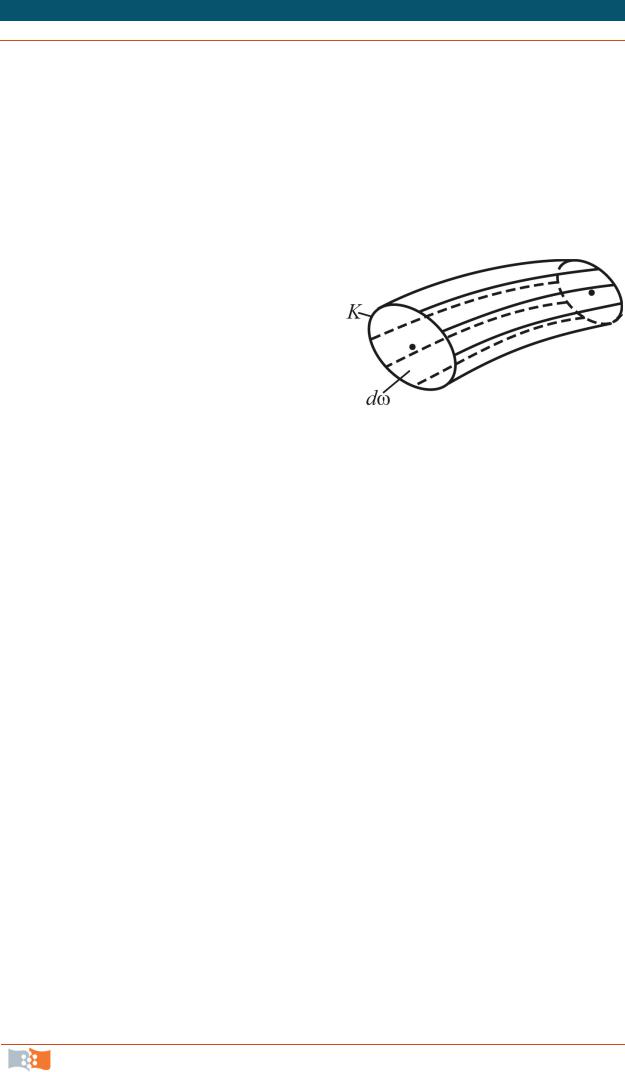
Если в потоке жидкости наметить точку и выделить вокруг нее элементарную площадку d , ограниченную пространственным контуром K (рис. 4.10), то совокупность линий тока, проведенных через все точки элементарной площадки d , образует трубку тока, математический аналог элементарной струйки.
В случае установившегося движения элементарная струйка обладает следующими тремя свойствами:
так как линии тока при установившемся движении жидкости с течением времени не меняют своей формы, то и струйка тока является неизменной во времени;
так как боковая поверхность струйки образована линиями тока, вдоль которых одна за другой скользят частицы жидкости, то проникновение жидкости через боковую поверхность струйки невозможно. Элементарная струйка как бы заключена в жесткие, не изменяющиеся во времени, водонепроницаемые стенки, не имеющие толщины;
так как площадь поперечного сечения элементарной струйки считается бесконечно малой, то величину скорости и давления для всех точек данного
поперечного сечения струйки следует считать одинаковыми. |
|
||||||
Так как |
для |
точки |
с положительным |
значением |
координат |
||
сos V x |
2 |
0 , а |
сos V |
x 0 , то скорость образует с осью x угол /2 и, |
|||
|
|
|
1 |
|
1 |
|
|
следовательно, движение происходит против часовой стрелки. |
|
||||||
Пример. |
Движение |
жидкости задано |
проекциями |
скоростей |
|||
V1 x1 t , V2 x2 t , V3 0 . Найти линии тока и траектории. |
|
||||||
Движение плоское (V3 0 ) и неустановившееся, т. к. V1 и V2 |
зависят от |
||||||
координат и времени. Следовательно, траектории и линии тока здесь не совпадают.
Интегрируя дифференциальное уравнение линий тока (4.5)
Гидрогазодинамика. Учеб. пособие |
66 |
4.КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
4.3.Основные кинематические элементы движения жидкости
dx1 / x1 t dx2 / x2 t
для фиксированного t , получим
x1 t x2 t C ,
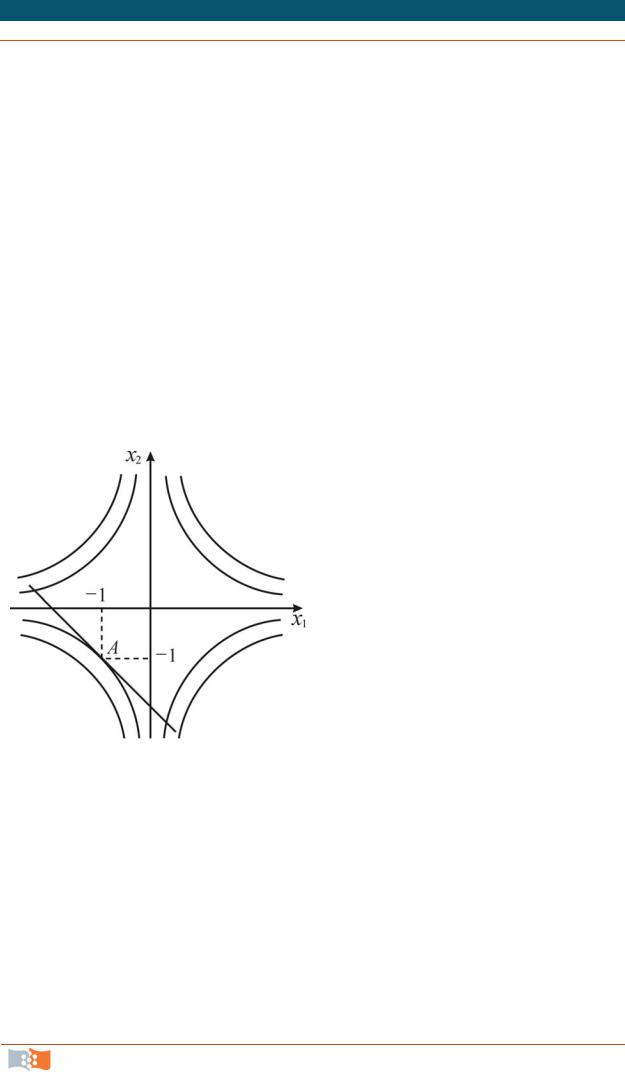
т. е. линии тока в каждый момент времени представляют собой семейство гипербол (рис. 4.11).
Для определения траекторий необходимо проинтегрировать уравнения линий тока:
dx1 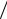 dt x1 t ; dx2
dt x1 t ; dx2 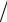 dt x2 t ,
dt x2 t ,
или, в явном виде,
dx1  dt x1 t ; dx1
dt x1 t ; dx1 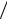 dt x1 t .
dt x1 t .
|
|
Каждое из этих уравнений |
||||
|
|
представляет собой линейное не- |
||||
|
|
однородное уравнение с постоян- |
||||
|
|
ными коэффициентами. |
Решение |
|||
|
|
их дает, как известно из математи- |
||||
|
|
ки, следующее выражение: |
|
|||
|
|
t |
t |
|
|
|
|
|
x1 C1e |
1, |
|
|
|
|
|
t |
|
|
|
(4.6) |
|
|
t |
|
|
|
|
|
|
x2 C2e |
1. |
|
|
|
|
|
Траекторию, которую опи- |
||||
|
|
сывает частица жидкости, нахо- |
||||
|
|
дящаяся в момент времени в точке |
||||
Рис. 4.11 |
|
А ( 1, 1), найдем после опреде- |
||||
|
ления постоянных |
С1 и |
С2 . |
Для |
||
|
|
|||||
этого подставим в (4.6) значения t 0, |
x1 |
1, x2 1, получим С1 |
С2 |
0 . |
||
Следовательно, для искомой траектории |
x1 t 1, x2 t 1 или, исключая |
|||||
время, x1 x2 2 , т. е. траектория частицы А есть прямая линия. |
|
|
||||
Вихревое движение. Вектор, |
равный удвоенному вектору |
угловой |
||||
скорости частицы, называется вихрем и обозначается rot V 2 . Вихрь характеризует вращение частиц вокруг некоторой оси. Вращательное движение жидкости с наличием компонентов вихря называется вихревым. Вихревое движение может быть плоским и пространственным.
Гидрогазодинамика. Учеб. пособие |
67 |
4.КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
4.3.Основные кинематические элементы движения жидкости
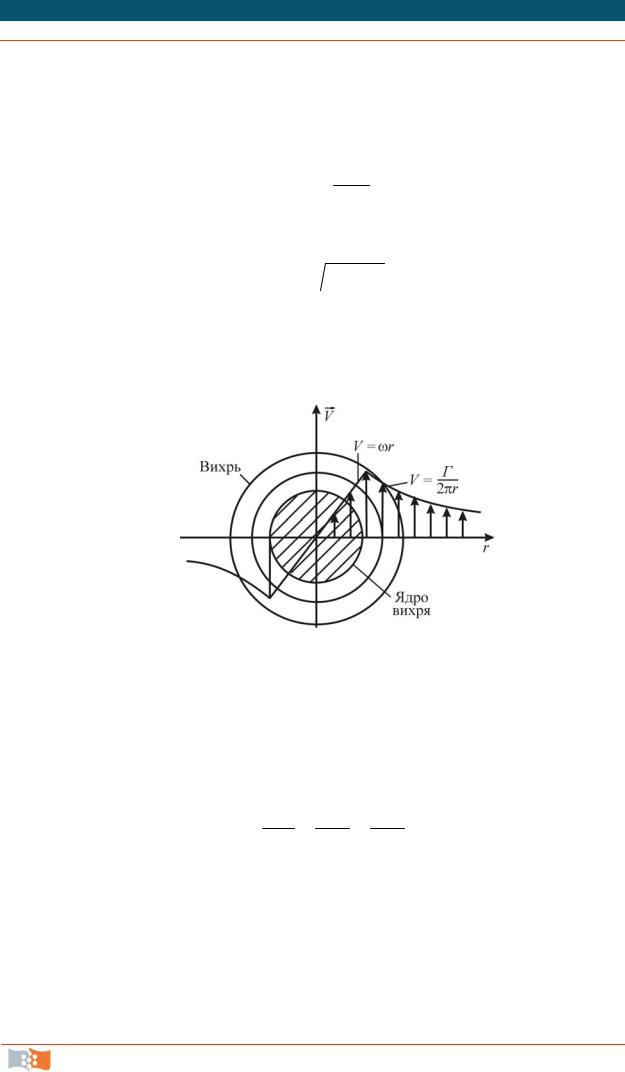
Пример. Рассмотрим плоский вихрь (рис. 4.12), линии тока и траектории которого представляют собой концентрические окружности с центром в начале координат.
Можно также показать, что скорости, вызванные плоским вихрем, определяются из выражения
V , 2 r
где Г циркуляция; r расстояние от центра вихря,
r  x12 x22 .
x12 x22 .
Скорость в центре вихря теоретически (r = 0) должна равняться бесконечности, что не согласуется с опытами для реальной жидкости. Поэтому делается допущение, что некоторая область вокруг центра вихря (ядро вихря) вращается как твердое тело, т. е. скорости в ядре пропорциональны радиусу.
Рис. 4.12
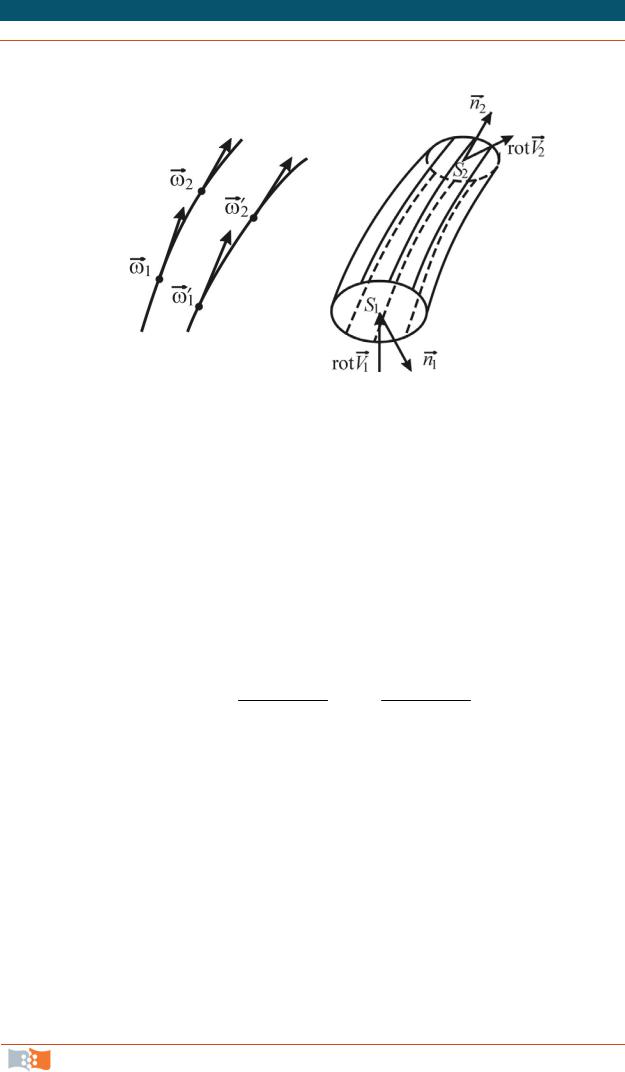
Если в данный момент времени можно провести геометрические линии, касательные к векторам угловых скоростей частиц, то эти линии будут называться вихревыми (рис. 4.13, а).
Дифференциальные уравнения вихревых линий по аналогии с уравнениями линий тока могут быть записаны в виде
dx1 dx2 dx3 , d 1 d 2 d 3
где dx1, dx2, dx3 проекции элементарного участка вихревой линии в декартовой системе координат; d 1, d 2, d 3 проекции угловой скорости.
Совокупность вихревых линий, проведенных через точки произвольного замкнутого контура, образует вихревую трубку (рис. 4.13, б). Объем жидкости, заключенный внутри вихревой трубки, называется вихревым шнуром, например, ядро вихря, все точки которого вращаются с постоянной угловой
Гидрогазодинамика. Учеб. пособие |
68 |
4.КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
4.3.Основные кинематические элементы движения жидкости
а |
б |
Рис. 4.13
скоростью. Остальная часть плоского вихря, находящаяся вне ядра, движется по круговым траекториям без поворота (вращения) частиц. Это можно показать на примере.
Пример. Определить угловые скорости вращения частиц в поле плоского вихря.
Проекции вектора угловой скорости вращения вокруг осей х1 и х2 равны нулю, т. к. V3 0 , а V1 и V2 не зависят от координаты x3 . Подставив зна-
чения
V1 |
x2 |
|
; V2 |
|
x1 |
|
||
2 x2 |
x2 |
|
2 x2 |
x2 |
|
|||
|
1 |
2 |
|
|
|
1 |
2 |
|
в формулу
|
1 |
|
V2 |
|
V1 |
|
, |
|
|
|
|||||||
|
2 |
|
x |
|
x |
2 |
|
|
|
|
|
1 |
|
|
|
|
|
получим = 0. Таким образом, понятия «вихрь» и «вращение частиц» неоднозначны и смешивать их нельзя.
В первом случае частицы движутся поступательно по траекториям – концентрическим окружностям, а во втором – вращаются относительно соответствующей (мгновенной) оси.
Гидрогазодинамика. Учеб. пособие |
69 |
4.КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
4.3.Основные кинематические элементы движения жидкости
Следовательно, при круговом движении может не быть вращения частиц и, наоборот, оно может иметь место при прямолинейном движении.
Влияние вихревой трубки на жидкость характеризуется ее интенсивно-
стью, т. е. потоком вектора вихря rotV через поперечное сечение вихревой трубки. Интенсивность i определяется по выражению
|
i |
rot V ndS , |
|
|
S |
где n |
нормаль к поперечному сечению S трубки. |
|
В случае если вихри непрерывно распределены по поверхности, они образуют вихревой слой. Идеализированный вихревой слой (толщина его стремится к нулю при неизменной интенсивности) называется вихревой пеленой.
Вихрь скорости, а также угло- |
|
|
вую скорость и интенсивность вихре- |
|
|
вой трубки измерить непосредственно |
|
|
нельзя. Наглядно представить интен- |
|
|
сивность можно, используя такое |
|
|
фундаментальное понятие, как цирку- |
|
|
ляция скорости. |
|
|
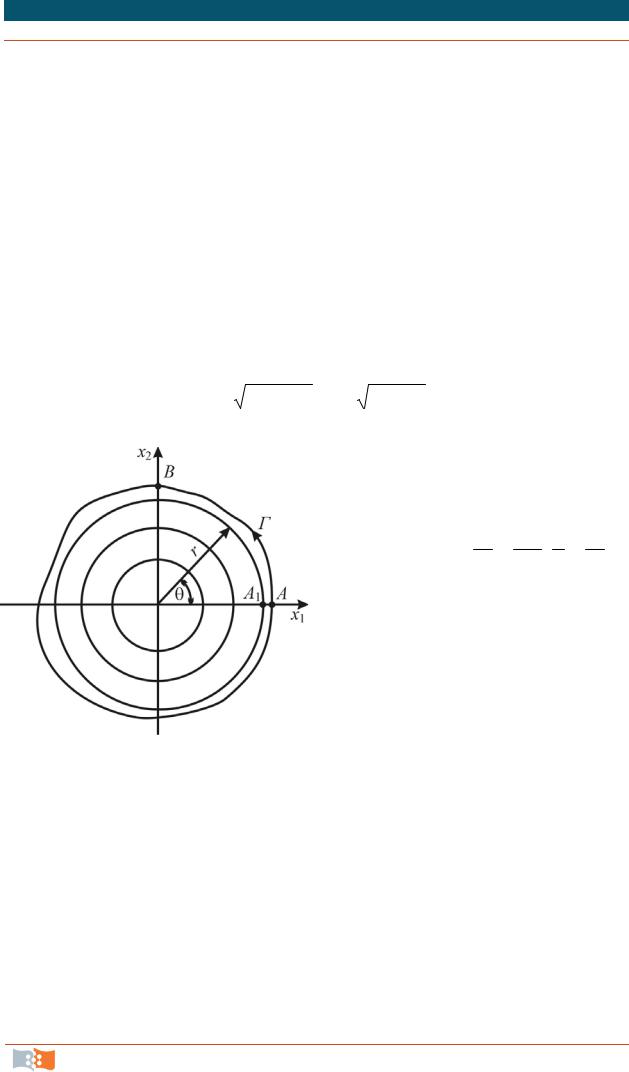
Циркуляция скорости представ- |
|
|
ляет собой криволинейный интеграл |
|
|
по контуру (рис. 4.14) от скалярного |
|
|
произведения вектора скорости V на |
Рис. 4.14 |
|
дифференциал направленного отрезка |
||
|
||
дуги контура dr : |
|
|
|
|
ABV dr . |
|
Раскрыв |
скалярное |
|
произведение, |
получим |
B
V1dx1 V2dx2 V3dx3 . Для замкнутого контура циркуляции вектора
A
скорости определяются контурным интегралом
V d r |
V1 dx 1 V 2 dx 2 V 3 dx 3 . |
L |
L |
Пример. Вычислить циркуляцию скорости по контуру, соединяющему точки с координатами А(х1, 0) и В(0, х2) в потоке жидкости, который задан проекциями скорости
V1 |
|
ax1 |
, V2 |
|
ax2 |
, V3 |
0 , |
|||
x2 |
x2 |
x2 |
x2 |
|||||||
|
|
|
|
|
|
|||||
|
|
1 |
2 |
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|||||
Гидрогазодинамика. Учеб. пособие |
|
|
|
|
70 |
|||||
4.КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
4.3.Основные кинематические элементы движения жидкости
где а некоторая константа.
В безвихревом потоке циркуляцию скорости выразим через потенциал скоростей, поскольку V1dx1 V2 dx 2 V3 dx3 d , т. е.
d K1 K2 ,
K
где K1 и K2 – значения потенциальной функции на концах рассматри-
ваемого контура.
Течение жидкости в данном случае является плоским, установившимся
и, т. к. V2 V1 (т. е. 3 = 0), потенциальным (безвихревым). При этом по-
x1 x2
тенциал φ можно определить по скорости потока
V V 2 |
V 2 |
a / |
x 2 |
x 2 |
a / r , |
1 |
2 |
|
1 |
2 |
|
где r полярный радиус
точки (рис. 4.15). Угол находят из соотношения
сos VV2 axr22 ar xr2 .
Отсюда следует, что вектор
скорости V перпендикулярен полярному радиусу точки, т. е.
Vr 0,
VS V a 1 r S r S
Рис. 4.15 |
Проинтегрировав последнее |
|
уравнение, найдем |
||
a . |
||
|
Этому значению соответствует функция тока
a ln r .
Отсюда уравнение линий тока: a ln r C . Согласно этому уравне-
нию, такие линии представляют собой окружности r C с центрами в начале координат.
Найдем циркуляцию скорости:
Гидрогазодинамика. Учеб. пособие |
71 |
4.КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
4.3.Основные кинематические элементы движения жидкости
d B A a |
|
0 a . |
A B |
2 |
2 |
Если подсчитать величину этой циркуляции по любому замкнутому контуру, охватывающему начало координат, то окажется, что
d A1 A .
K
Отсюда следует, что a /2 . Физически этот случай, согласно теореме Стокса (см. ниже), соответствует наличию в особой точке r 0 вихревой
нити интенсивностью, равной циркуляции Г. При этом вне вихревой нити течение будет безвихревое.
4.4. Полеускорений
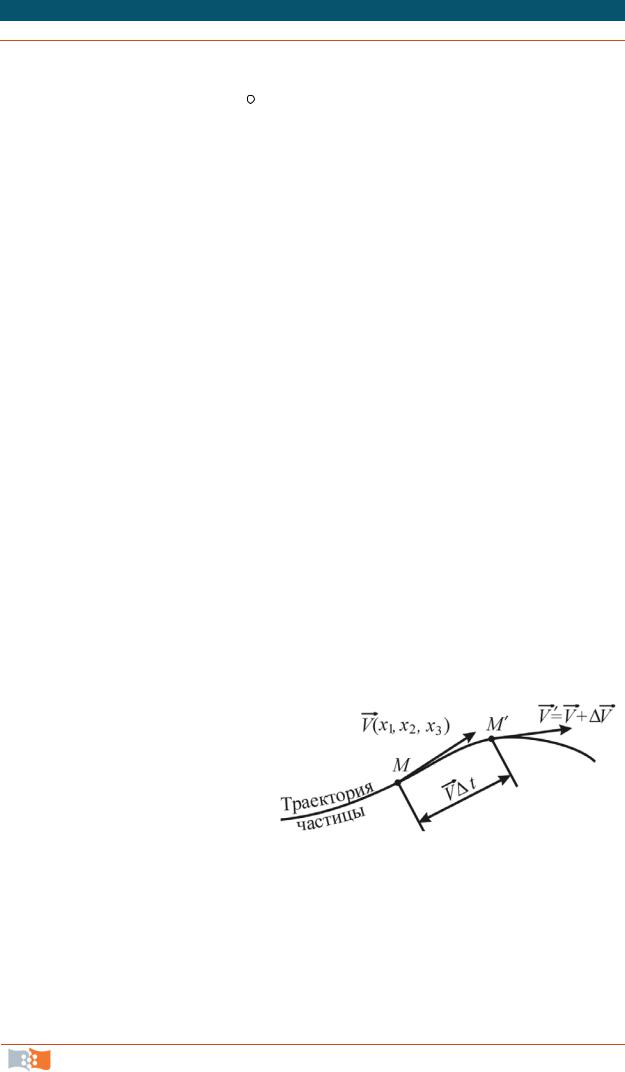
На основе функциональных связей (4.1) (4.2) можно получить общее выражение для полного ускорения жидкой частицы. Ускорение – это векторная производная по времени от скорости.
Известно, что ускорение перемещающейся фиксированной точки определяется пределом
|
|
|
|
lim |
V V |
dV |
, |
|
|
|
|
t 0 |
t |
dt |
|
где |
V , |
V |
скорости |
|
|
|
|
частицы |
при |
ее |
перемещении |
|
|
|
|
из точки |
M |
в точку M |
за |
|
|
|
|
промежуток t (рис. 4.16). |
|
|
|
|
|||
В механике жидкости ус- |
|
|
Рис. 4.16 |
||||
корение, |
определенное по |
ме- |
|
|
|
||
тоду Лагранжа, выражается частной производной по времени
Гидрогазодинамика. Учеб. пособие |
72 |

4.КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
4.4.Поле ускорений
V V
t
(точка над буквой обозначает производную по времени). ПроизводнаяVt выражает изменение скорости в фиксированной точке пространства,
т. к., по Лагранжу, переменные а, b, c в каждой точке разные. Здесь же в конечном счете нужно знать, как изменяется скорость данной частицы жидкости.
В эйлеровых переменных вектор скорости представляет собой в общем случае вектор-функцию вектора-радиуса точек пространства и времени. Следовательно, индивидуальную производную
V ddtV
можно рассматривать как сложную функцию от времени t (нестационарное поле скоростей в явном виде) и через посредство координат х1, х2, х3 движущейся точки. Тогда
|
|
|
|
|
|
|
|
|
|
V |
|
|
V |
dx3 |
|
|
|
V dV |
|
V |
V dx1 |
|
dx2 |
|
, |
||||||||
|
|
|
||||||||||||||
|
|
|
dt |
|
t |
|
x dt |
|
x dt |
|
x dt |
|
||||
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
3 |
|
|
|
или, заменив |
dx1 |
, |
dx2 |
, |
dx3 |
|
обозначениями проекции скорости на оси ко- |
|||||||||
dt |
dt |
dt |
||||||||||||||
ординат |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
dx1 V , |
|
dx2 |
|
V , |
dx3 |
|
V , |
|
|||||
|
|
|
|
|
|||||||||
dt |
1 |
|
dt |
2 |
|
dt |
3 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||||
получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V |
|
|
|
V |
|
|
V |
|
|
V |
|
|
V |
|
V1 |
|
V2 |
|
|
|
V3 |
|
. |
(4.7) |
||
t |
x |
x |
|
x |
|||||||||
|
|
1 |
|
2 |
3 |
|
|
||||||
Спроецировав V на оси координат, имеем
Гидрогазодинамика. Учеб. пособие |
73 |
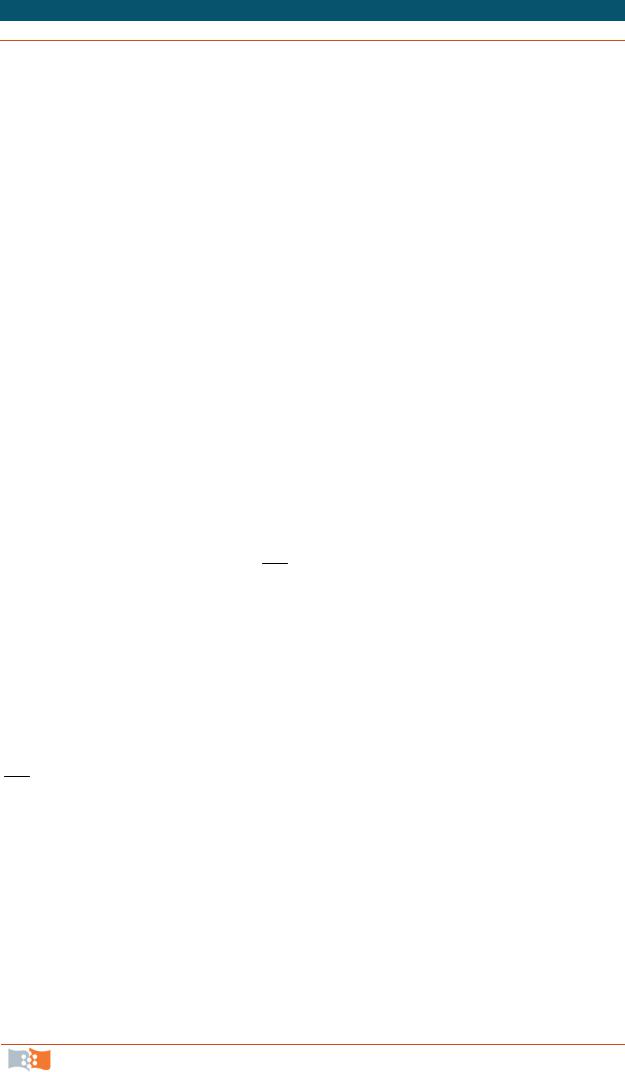
4.КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
4.4.Поле ускорений
V1 |
dV1 |
|
V1 |
|
V1 |
|
V1 |
|
V1 |
|
|
|
|||
dt |
|
t |
V1 x |
V2 x |
2 |
V3 x |
, |
|
|||||||
|
|
dV |
|
V |
|
1 |
|
|
|
3 |
|
|
|
||
V2 |
|
|
V1 |
V |
V2 |
V |
V3 |
V |
|
|
(4.8) |
||||
2 |
2 |
2 |
|
|
2 |
2 |
, |
||||||||
|
|
dt |
|
t |
|
x1 |
|
x2 |
|
x3 |
|
|
|||
V |
dV3 |
|
V3 |
V |
V3 |
V |
V3 |
V |
V3 |
. |
|
||||
3 |
|
dt |
|
t |
1 x |
2 x |
2 |
3 x |
|
|
|
||||
|
|
|
|
|
|
1 |
|
|
|
|
3 |
|
|
|
|
Введя вектор – дифференциальный оператор
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
|
|
|
|
|
|
|
x |
x |
2 |
x |
||||||
|
|
|
|
1 |
|
|
|
3 |
и перейдя от проекции к векторному выражению, получим формализованное выражение ускорения
V |
dV |
|
V V |
V . |
(4.9) |
||
|
|
|
|
|
|
|
|
|
|
dt |
|
t |
|
|
|
Отсюда видно, что, по Эйлеру, ускорение можно разделить на две составляющие. Первое слагаемое Vt выражает изменение скорости со време-
нем в точке, т. е. при фиксированных координатах, называется локальным ускорением и характеризует нестационарность поля скоростей. Локальное ускорение равно нулю в любой момент времени, если поле скоростей стационарно (в этом случае траектории частиц жидкости совпадают с линиями тока) или когда в данной точке скорость достигает своего максимального (или минимального) значения.
Следует обратить внимание, что в эйлеровых переменных, даже когдаVt = 0, ускорение все же имеется. Примером может служить вода, текущая с
постоянной скоростью по кругу: ускорение есть и тогда, когда скорость в данной точке не изменяется. Причина в том, что скорость воды в данный момент в другой момент будет иметь другое направление – это центростремительное ускорение.
Второе слагаемое в правой части выражения (4.9) образуется за счет изменения координат точки, соответствующего перемещению (конвекции) ее в поле скоростей, и называется конвективным ускорением, которое характе-
ризует неоднородность поля. Конвективное ускорение Vконв 0 тогда и только тогда, когда поле скоростей однородно, т. е. скорости во всех точках рас-
Гидрогазодинамика. Учеб. пособие |
74 |
4.КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
4.4.Поле ускорений
сматриваемой области одни и те же (например в начале движения тела в неподвижной жидкости).
В механике жидкости и газа оператор индивидуальной производной по времени
d... |
... V ... , |
(4.10) |
|
|
|
|
|
dt |
t |
|
|
использованный в (4.9) применительно к вектору скорости, может применяться также к скалярным функциям (например температуре, плотности и т. д.) и к тензорным величинам, связанным с движущейся частицей жидко-
сти. Выражение (4.10) называют еще субстациональной производной, т. к. она вычисляется при наблюдении за движением материальной частицы.
4.5.Кинематическийанализдвиженияжидкойчастицы
Вотличие от твердого тела жидкость представляет собой деформируемую среду, т. е. появляется дополнительная (по сравнению с «твердым телом») скорость, обусловленная деформацией жидкого объема. Следовательно, скорости в отдельных точках пространства, заполненного движущейся жидкостью, могут быть неодинаковыми как по величине, так и по направлению.
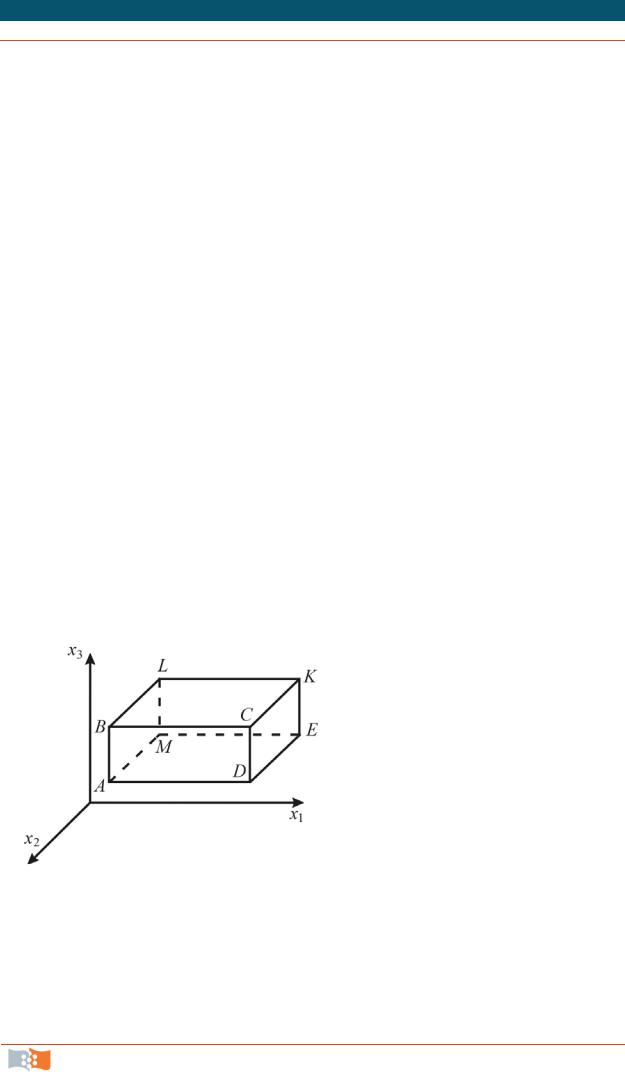
Рис. 4.17
ращения:
Пусть имеется некоторый элементарный жидкий объем. Начальную форму этого объема удобнее всего представить в виде прямоугольного параллелепипеда ABCDEKLM , ребра которого параллельны осям координат (рис. 4.17). Координаты вершины A параллелепипеда х1, х2, х3, а размеры его ребер – dx1, dx2, dx3. Проекции вектора скорости в вершине A паралле-
лепипеда обозначим V1, V2, V3. В других вершинах за счет дефор-
мационного движения скорости получают соответствующие при-
Гидрогазодинамика. Учеб. пособие |
75 |

4.КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
4.5.Кинематический анализ движения жидкой частицы
V1 |
dx |
; |
V |
dx |
|
; |
V |
dx |
; |
V |
dx |
; |
V2 |
dx |
и т. п. |
|
x |
x |
1 |
|
1 |
2 |
x |
||||||||||
1 |
|
2 |
|
2 |
|
x |
3 |
|
x |
1 |
|
2 |
|
|||
1 |
|
|
|
|
|
|
3 |
|
|
1 |
|
|
2 |
|
|
|
Проекции скорости в точке D можно записать следующим образом:
V |
V |
|
|
V1 |
dx |
; |
V |
V |
|
V2 dx |
; V |
|
|
|
V |
|
V3 |
dx . |
||||
1D |
1 |
|
x |
|
1 |
2D |
2 |
|
x |
1 |
3D |
|
3 |
|
|
x |
1 |
|||||
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
Проекции скорости в точке B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
V |
V |
|
V1 |
dx |
|
; |
V |
V |
|
V2 |
dx |
; V |
|
|
|
V |
|
|
V3 |
dx . |
||
1B |
1 |
|
x |
3 |
|
2B |
2 |
|
x |
3 |
3B |
|
3 |
|
|
x |
3 |
|||||
|
|
|
|
3 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
3 |
|
Для точки С получим проекции скорости VС |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
V |
V |
|
|
V1 |
x V |
V1 dx + |
V1 |
dx |
; |
|
||||||||||
|
|
|
1C |
|
1D |
|
|
x |
3 |
|
1 |
x |
1 |
|
|
x |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
1 |
|
|
|
|
3 |
|
|
|
|
|
|
V |
|
V |
|
V2 |
x V |
V2 |
dx |
|
+ V2 |
dx |
; |
|
|||||||||
|
|
2C |
|
2D |
|
|
x |
3 |
|
2 |
x |
1 |
|
|
x |
|
|
3 |
|
|||
|
|
|
|
|
|
|
|
3 |
|
|
|
1 |
|
|
|
|
3 |
|
|
|
|
|
|
V |
V |
|
|
V3 |
x V |
V3 |
dx |
+ |
|
V3 |
dx |
|
, |
|
|||||||
|
|
|
3C |
|
3D |
|
|
x |
3 |
|
3 |
x |
1 |
|
|
x |
|
3 |
|
|
||
|
|
|
|
|
|
|
|
3 |
|
|
|
1 |
|
|
|
|
3 |
|
|
|
|
|
и, наконец, для точки K имеем
V1K
V2K
V3K
V |
|
V1 |
x |
|
V |
V1 |
dx |
+ |
V1 |
x |
|
+ V1 |
dx ; |
||||||||
1C |
|
x |
2 |
|
|
2 |
1 |
x |
1 |
|
x |
2 |
2 |
|
|
x |
3 |
|
|||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
3 |
|
|
|||
V |
|
V2 |
x |
|
|
V |
V2 |
dx |
+ |
V2 |
x |
|
|
+ |
V2 |
dx |
; |
||||
2C |
|
x |
2 |
|
2 |
2 |
x |
1 |
|
x |
2 |
|
2 |
|
x |
3 |
|
||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
3 |
|
|
|||
V |
|
V3 |
x |
|
|
V |
V3 |
dx |
+ |
V3 |
dx |
|
|
+ |
V3 |
dx |
. |
||||
3C |
|
x |
2 |
|
2 |
3 |
x |
1 |
|
x |
2 |
2 |
|
x |
3 |
|
|||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
3 |
|
|
||||
Исследуем частные случаи движения и деформации рассматриваемого элемента.
Параллельный перенос. В данном случае элемент, не изменяя своей формы, перемещается поступательно, подобно твердому телу, и все его точки поэтому имеют одинаковую скорость.
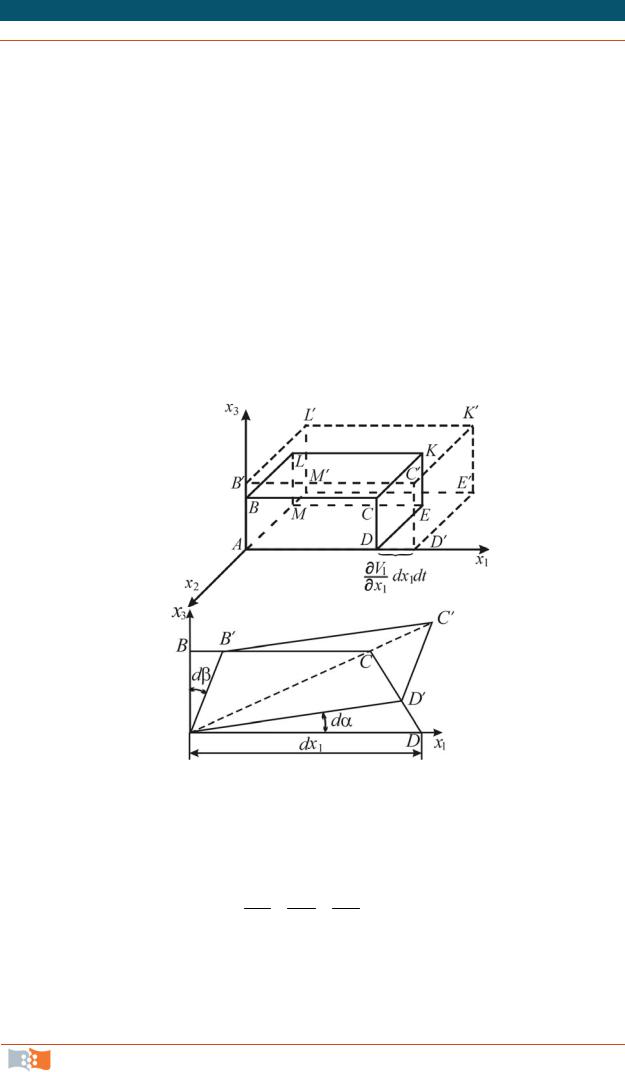
Объемная деформация. Этот вид деформации связан с удлинением граней. За время dt грань AD удлиняется на величину DD , равную
Гидрогазодинамика. Учеб. пособие |
76 |
4.КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
4.5.Кинематический анализ движения жидкой частицы
V |
dx dt , где |
V1 |
dx1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
|
|
скорость деформации (рис. 4.18). Приращение объема |
||||||||||||||||||||||
x1 |
|||||||||||||||||||||||||
x |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
жидкого элемента |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
V1 |
|
|
|
|
|
|
V2 |
|
|
|||
|
W WA B C D E K L M WABCDEKL |
|
dx1 |
|
|
|
dx1dt |
dx2 |
|
|
dx2dt |
|
|||||||||||||
|
|
x1 |
x2 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
V3 |
|
|
|
|
V1 |
|
V2 |
|
V3 |
|
|
|
|
|
|||||||
|
dx3 |
|
dx3dt dx1dx2dx3 |
|
x |
|
x |
|
x |
dx1dx2dx3dt. |
|
||||||||||||||
|
x |
|
|
||||||||||||||||||||||
|
|
|
|
3 |
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
3 |
|
|
|
|
|
||
|
Относительная объемная деформация |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
W |
|
V1 |
|
V2 |
|
|
V3 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
dW |
|
x |
|
|
|
x |
2 |
|
x |
dt . |
|
|
|
|
(4.11) |
|||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|||
А
Рис. 4.18 |
Рис. 4.19 |
Скорость относительной объемной деформации
V1 V2 V3 divV .
x1 x2 x3
Для несжимаемой жидкости
Гидрогазодинамика. Учеб. пособие |
77 |

4.КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
4.5.Кинематический анализ движения жидкой частицы
V1 |
|
V2 |
|
V3 |
0 . |
(4.12) |
||
x |
|
x |
2 |
|
x |
3 |
|
|
1 |
|
|
|
|
|
|
||
Уравнение (4.12) представляет собой уравнение неразрывности для несжимаемой жидкости.
Чистая деформация. Этот вид деформации обусловлен скашиванием углов (рис. 4.19). Грань AD повернется на угол dα. Поворот происходит вследствие того, что скорость V3D точки D больше скорости V3A точки A
на величину |
V3 |
dx |
. Тогда деформация DD´ равна |
x3 |
dx dt |
. Вследствие |
|
x |
|||||||
x |
1 |
1 |
|||||
|
1 |
|
|
1 |
|
|
малости углов dα и dβ можно считать, что
d tgd DD V3 dt , dx1 x1
d tgd BB V3 dt . dx3 x3
Условие чистой деформации (скашивания углов) d = d , откуда
V3 V1 .
x1 x3
Скорость чистой деформации:
вплоскости x1 x3 |
|
|
|
|
1 |
|
V |
3 |
|
|
|
|
V |
|
|
|
|
|
|
|
|
S |
31 |
S |
13 |
|
|
|
|
|
|
|
1 |
|
|
; |
|
||||
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
2 |
|
x1 |
|
x3 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
вплоскости x1 x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
1 |
|
V |
2 |
|
|
|
V |
|
|
|
|
|
|
||
|
S |
12 |
S |
21 |
|
|
|
|
|
1 |
|
|
; |
|
||||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
2 |
|
x1 |
|
x2 |
|
|
|
|
(4.13) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
вплоскости x2 x3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
1 |
|
V |
3 |
|
|
|
V |
2 |
|
|
|
|
|
|
|
S |
23 |
S |
32 |
|
|
|
|
|
|
|
|
|
. |
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
2 |
|
x2 |
|
x3 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Квазитвердый поворот. В этом слу- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
чае элемент, не меняя формы, поворачива- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
ется как твердое тело на некоторый угол |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
(рис. 4.20). Скорость VB точки B больше |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
скорости в точке |
A , поэтому происходит |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
поворот ребра AB |
в положение AB : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 4.20
Гидрогазодинамика. Учеб. пособие |
78 |

4.КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
4.5.Кинематический анализ движения жидкой частицы
|
|
V |
|
V |
|
V1 dx |
|
. |
||
|
|
1B |
1A |
|
x3 |
3 |
|
|||
Тогда BB равно |
V |
|
|
а DD |
|
V3 |
dx1 dt . Вследствие малости |
|||
1 dx dt |
, |
|
|
|||||||
x1 |
||||||||||
|
x |
3 |
|
|
|
|
|
|
||
|
3 |
|
|
|
|
|
|
|
|
|
углов принимаем
d tgd DD V3 dt; dx1 x1
d tgd BB V1 dt. dx3 x3
Так как d = d при повороте, то
V1 V3 .
x3 x1
Соответствующий такому перекашиванию ребер поворот всей грани АBCD следует определять вращением ее средней линии – биссектрисы угла BAD . Угол, на который повернется биссектриса угла относительно перво-
начального положения, определяется полусуммой 12 d d . Следовательно,
угловая скорость ее вращения и вращения всего интересующего нас жидкого элемента будет:
относительнооси х2 :
относительнооси x1:
относительнооси x3:
|
|
|
1 |
|
V1 |
|
V3 |
|
|
|
|
|
; |
|
|||||||
|
2 |
|
2 |
|
x |
|
x |
|
|
|
|
|
|
|
|
3 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
V3 |
|
|
|
|
|
|||
|
V2 ; |
|
||||||||
1 |
|
2 |
|
x2 |
|
x3 |
|
|
(4.14) |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
V2 |
|
V1 |
|
|
|
||
|
. |
|
||||||||
|
3 |
|
2 |
|
x |
|
x |
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
Скорости 1 , 2 , 3 можно рассматривать как проекции некоторого
вектора на координатные оси. |
|
|
|
|
|
|
|
|
|
Вектор |
, имеющий проекции |
|
1 |
2 1 , |
|
2 2 2 , |
3 2 3 , является |
||
вихрем rotV |
с компонентами |
|
|
|
|
|
|
|
|
|
|
|
V3 |
|
V2 |
|
; |
|
|
|
|
|
|
||||||
|
1 |
|
x |
2 |
|
x |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
Гидрогазодинамика. Учеб. пособие |
79 |

4.КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
4.5.Кинематический анализ движения жидкой частицы
|
|
V1 |
|
|
V3 |
|
|
|
|
|
2 |
|
|
|
|
|
(4.15) |
||||
|
x |
x |
; |
|
|
|||||
|
|
|
3 |
|
|
1 |
|
|
|
|
|
|
|
|
|
V2 |
|
V1 |
|
||
|
|
|
|
|||||||
|
|
3 |
|
|
|
x |
|
x |
2 |
. |
|
|
|
|
|
|
1 |
|
|
|
|
Таким образом, угловая скорость квазитвердого вращения
|
|
(4.16) |
|
1 rotV. |
|
|
2 |
|
Гидрогазодинамика. Учеб. пособие |
80 |
4.КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
4.6.Движениежидкостивлокальномобъеме. ПерваякинематическаятеоремаКоши Гельмгольца
Из курса теоретической механики известно, что в общем случае движение твердого тела складывается из поступательного перемещения и вращения вокруг мгновенной оси, проходящей через произвольно выбранный полюс. Движение элементарного объема жидкости сложнее, так как, двигаясь в сплошном потоке, он непрерывно деформируется.
Рассмотрим вначале квазитвердое движение жидкости, т. е. случай движения воды, если ее заморозить до стадии льда. Выделим в жидкости произвольный элементарный объем (рис. 4.21) и разложим движение на составляющие. Особенностью квазитвердого движения является одинаковость угловых скоростей всех точек тела независимо от выбора полюса и размеров тела.
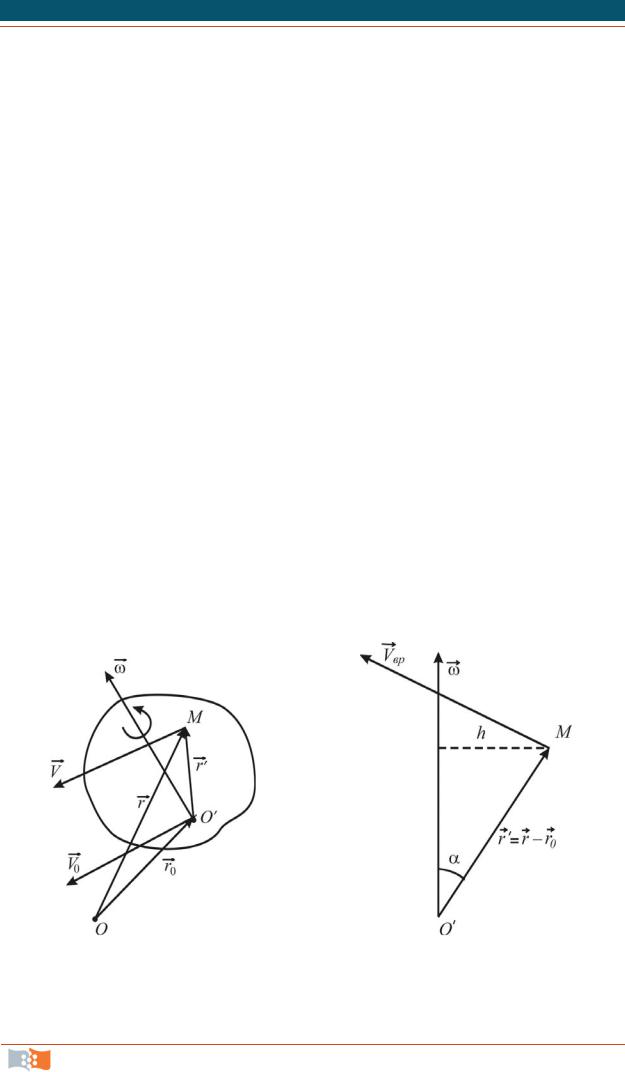
Рассмотрим движение фиксированной точки O (полюса) твердого тела
(рис. 4.21) и произвольной точки M заданными радиусами-векторами r0 |
и r ; |
r радиус-вектор точки M относительно полюса O . Очевидно, что r r0 |
r |
или r r r0. В каждый момент времени тело еще и поворачивается. Пусть |
|
вектор (рис. 4.21) есть угловая скорость в данный момент времени и пусть в этот же момент точка M имеет скорость V , а точка O скорость V0 . Тогда
V Vпост Vвр , |
|
|
(4.17) |
||
|
|
|
dr |
|
|
где Vпост V0 |
|
|
. |
||
dt |
|||||
|
|
|
|
||
Рис. 4.21 |
Рис. 4.22 |
Гидрогазодинамика. Учеб. пособие |
81 |

4.КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
4.6.Движение жидкости в локальном объеме. Первая кинематическая теорема Коши ( Гельмгольца
Скорость вращения Vвр точки M – это угловая скорость, умноженная на радиус вращения h (рис. 4.22):
|
|
|
|
|
(4.18) |
Vвр h r sin . |
|
||||
Скорость Vвр r и оси вращения , следовательно, |
|
||||
|
|
|
|
. |
(4.19) |
Vвр r |
r |
r0 |
|||
Тогда поле скоростей в твердом теле в общем случае его движения определяет классическая формула Эйлера
V V0 r r0 . |
(4.20) |
Рассматривая твердое тело как сплошную среду с определенным полем скоростей, найдем выражение вектора угловой скорости через скорости этого
поля. Для этого запишем поле скоростей в проекциях и найдем через скорости отдельных точек. Проекции (4.20):
V |
V |
|
x |
x |
x |
x |
, |
|
|||
1 |
o1 |
2 |
|
3 |
03 |
3 |
|
2 |
02 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V |
V |
|
|
x |
x |
|
x |
x |
, |
|
|
2 |
o2 |
3 |
1 |
01 |
1 |
|
3 |
03 |
|
(4.21) |
|
|
|
|
|
|
|
|
|
|
|
|
|
V |
V |
|
x |
x |
|
|
x |
x |
. |
|
|
3 |
o3 |
1 |
|
2 |
02 |
2 |
1 |
01 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Так как угловая скорость для всех точек твердого тела одна и та же, т. е. = const, V есть линейная функция координат х1, х2, х3. Составим производные от проекции скорости (4.21):
V3 |
|
V2 |
2 |
|
, |
|
|
||
rot V |
|
|
|||||||
x2 |
|
x3 |
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
V1 |
|
V3 |
|
|
|
rot V |
|
|
|
|
2 |
|
|
, |
|
||||
x3 |
|
x1 |
|
2 |
2 |
|
|
(4.22) |
|
|
|
|
|
|
|
|
|
|
|
V2 |
V1 |
|
|
|
rot V . |
|
|
||
2 |
3 |
|
|
||||||
x1 |
|
x2 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
Гидрогазодинамика. Учеб. пособие |
82 |
4.КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
4.6.Движение жидкости в локальном объеме. Первая кинематическая теорема Коши ( Гельмгольца
Дифференциальную операцию rot называют пространственной производной в векторном поле и определяют проекциями, представляющими собой комбинацию частных производных, записанных в левой части равенств (4.22);
rot V называют ротором скорости, или вихрем. В рассматриваемом случае движения твердого тела формулы (4.22) можно записать в векторном виде
|
|
(4.23) |
|
1 rot V . |
|
|
2 |
|
В общем случае деформируемой среды – жидкости понятие угловой скорости для целого объема становится бессмысленным, и рассматривать разложение движения жидкости можно только в малом, элементарном ее
объеме в окрестности данной точки M (в локальном объеме рис. 4.23). В случае локального объема поле скоростей в нем можно приближенно считать таким же, как в твердом теле.
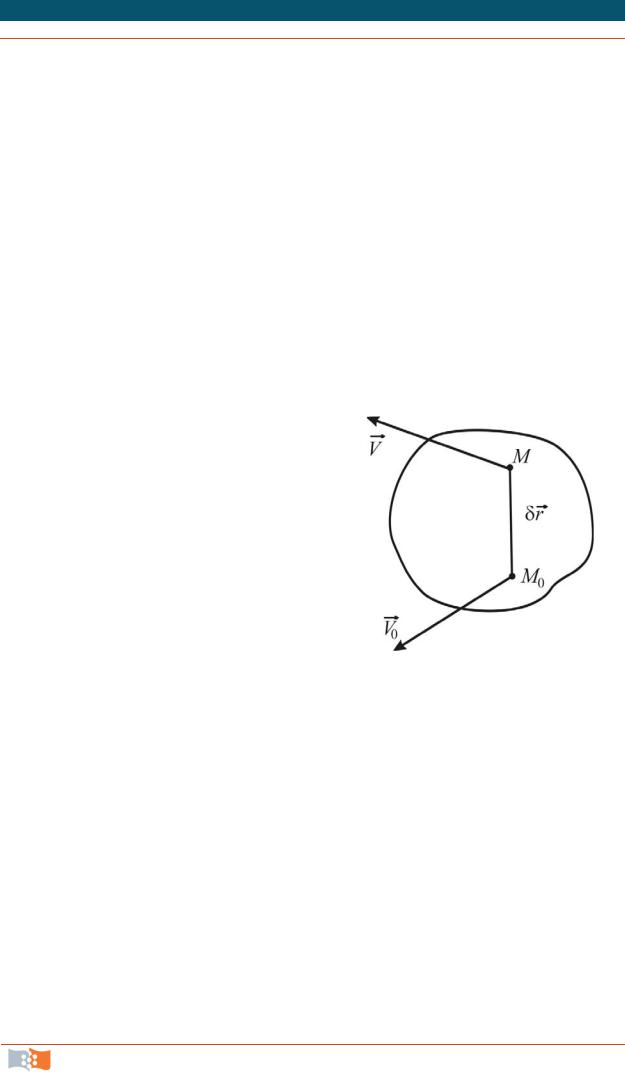
Примем за полюс точку M0 и рассмотрим движение частицы (матери-
альной точки) M , расположенной |
на бесконечно |
малом |
расстоянии r |
||||||||||||||
(рис. 4.23). Знак |
обозначает диффе- |
|
|
|
|
|
|
|
|||||||||
ренциал в пространстве в данный фик- |
|
|
|
|
|
|
|
||||||||||
сированный момент времени (прираще- |
|
|
|
|
|
|
|
||||||||||
ние величины во времени обозначается |
|
|
|
|
|
|
|
||||||||||
символом d ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В точке М |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V V0 V V0 , |
|
(4.24) |
|
|
|
|
|
|
|
||||||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V V0 V x1 |
V |
|
x2 |
V |
x3 0 |
|
|
|
|
|
|||||||
x |
|
|
|
|
|
|
|
|
|||||||||
x |
|
2 |
|
|
x |
3 |
|
|
|
|
|
|
|
|
|||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
приращение скорости. Уравнение |
|
|
|
|
|
Рис. 4.23 |
|||||||||||
(4.24) без учета малых второго порядка в |
|
|
|
|
|
|
|
||||||||||
проекциях будет иметь вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
V1 |
Vo1 |
|
V1 x1 |
|
V1 x2 |
V1 x3 , |
|
|
|||||||||
|
|
|
|||||||||||||||
|
|
|
|
|
x1 |
|
|
x2 |
|
|
x3 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V2 x |
|
V2 x |
|
|
V2 x |
|
|
|
||||
V |
V |
|
|
|
|
|
|
, |
|
||||||||
2 |
o2 |
|
|
x1 |
1 |
|
x2 |
2 |
|
x3 |
3 |
|
(4.25) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V3 x |
|
V3 x |
|
|
V3 x |
|
|
|
||||
V |
V |
|
|
|
|
2 |
|
. |
|
||||||||
3 |
o3 |
|
|
x1 |
1 |
|
x2 |
|
x3 |
3 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Переход от описания локальной деформации упругого твердого тела (по закону Гука) к описанию деформации жидкой среды (по закону Ньютона)
Гидрогазодинамика. Учеб. пособие |
83 |

4.КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
4.6.Движение жидкости в локальном объеме. Первая кинематическая теорема Коши ( Гельмгольца
требует замены деформации упругого тела на скорость деформации, которая является фундаментальным понятием движения жидкого объема.
Для выделения деформационного движения из (4.25) вычтем компоненты, составляющие квазитвердое движение:
V |
|
V |
x |
x , |
|
||
к т |
|
ox |
2 3 |
3 |
2 |
|
|
1 |
1 |
|
|
|
|
||
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
V |
|
V |
x |
x , |
|
||
к т |
|
ox |
3 1 |
1 |
3 |
|
|
|
2 |
2 |
|
|
|
(4.26) |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
V |
|
V |
x |
x . |
|
||
к т3 |
ox3 |
1 2 |
2 1 |
|
|
||
|
|
|
|
|
|
|
|
Сучетом(4.22) получимпроекциискоростейдеформационногодвижения:
V |
S x |
S x |
S x , |
|
|||||
деф1 |
11 |
1 |
12 |
2 |
13 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
V |
S x S |
x |
S |
x |
, |
|
|||
деф |
21 |
1 |
22 |
2 |
23 |
3 |
|
|
|
2 |
|
|
|
|
|
|
|
|
(4.27) |
|
|
|
|
|
|
|
|
|
|
V |
S x |
S |
x |
S |
x |
, |
|
||
деф3 |
31 |
1 |
32 |
2 |
33 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где
|
|
V1 |
|
|
|
|
V2 |
|
|
|
V3 |
|
|
|
|
|
1 |
|
V1 |
|
V2 |
|
||||||
S11 |
|
|
|
; S22 |
|
|
|
; S33 |
|
; S12 S21 |
|
|
|
|
|
|
|
|
|
|||||||||
x1 |
x |
|
x |
2 |
|
x2 |
x1 |
; |
||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 V2 |
|
V3 |
|
|
|
|
1 |
|
V3 |
|
V1 |
|
||||||||||
|
S |
|
S |
|
2 |
|
x3 |
|
x2 |
; |
S |
S |
|
|
2 |
|
|
x1 |
|
|
|
|
. |
|
||||
|
23 |
|
32 |
|
|
|
|
31 |
13 |
|
|
|
|
x3 |
|
|||||||||||||
Таким образом, движение жидкого объема характеризуется полем скоростей:
V Vк т Vдеф;
в проекциях:
Гидрогазодинамика. Учеб. пособие |
84 |
4.КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
4.6.Движение жидкости в локальном объеме. Первая кинематическая теорема Коши ( Гельмгольца
|
|
|
|
|
|
|
|
V |
V |
x |
x |
2 |
S |
x |
S |
x |
2 |
S |
x , |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
1 |
|
o1 |
|
2 3 |
3 |
|
11 1 |
12 |
13 3 |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
V |
V |
x |
x |
|
S |
x |
S |
x |
|
|
S |
x |
|
, |
(4.28) |
|||||||||||
|
|
|
|
|
|
|
|
2 |
|
o2 |
|
3 1 |
1 |
3 |
|
21 1 |
22 |
2 |
23 3 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
V |
V |
x |
2 |
x |
S |
x |
S |
x |
2 |
S |
x |
, |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
3 |
|
o3 |
|
1 |
2 1 |
|
31 1 |
32 |
33 3 |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где |
|
|
|
1 S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
S x , x |
, x |
, t |
0 |
|
x2 |
S |
x2 |
S |
|
x2 2S |
|
x x |
2 |
2S x x |
3 |
2S |
23 |
x |
|
x |
|
|||||||||||||
1 |
2 |
3 |
|
|
2 |
11 |
1 |
22 |
2 |
33 |
3 |
|
12 |
1 |
|
|
13 |
1 |
|
|
|
2 |
|
3 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
функция деформации элемента объема, или тензор скоростей деформации. |
|
|||||||||||||||||||||||||||||||||
|
В векторной форме (4.28) записывают так: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
V V0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4.29) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
S r , |
|
|
|
|
|
|
|
|
|
|||||||||||
причем первые два слагаемых выражают скорости в квазитвердом и последнее – в деформационном движении, что соответствует первой кинема-
тической теореме Коши Гельмгольца: движение элементарного объема жидкости можно в каждый момент времени представить себе разложенным на квазитвердое и деформационное.
Рассмотрим квазитвердое движение. В каждой точке поля скоростей имеем скорость поступательного движения и угловую скорость вращения частицы жидкости, т. е. имеем поле угловых скоростей или поле вихрей (под вращением частицы жидкости понимают поворот частицы вокруг мгновенной оси).
Метод Эйлера наряду с описанием поступательного движения на основе понятия линии тока позволяет представить вращательное движение с помощью понятия вихревой линии.
Вихревой линией называется линия, в каждой точке которой вектор угловой скорости направлен к ней по касательной в данный момент времени. Наглядным примером вихревой линии может служить гибкий вал.
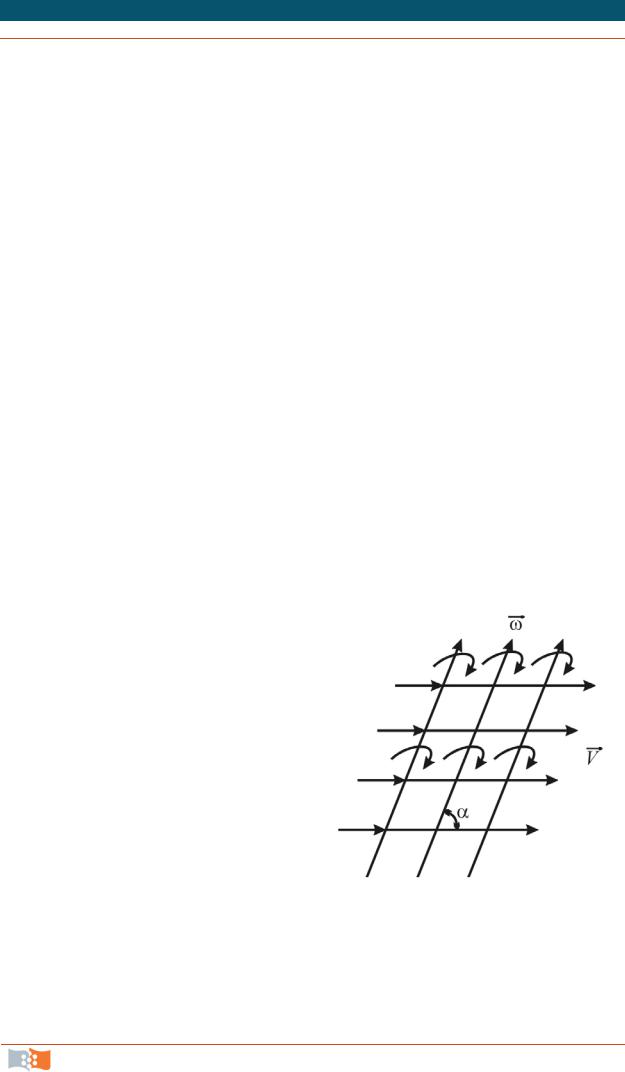
Таким образом, движение конечного объема жидкости может быть представлено совокупностью семейства линии тока и семейства вихревых линий (рис. 4.24). Угол можетбытьлюбым. Вчастности, при совпадении линий тока и вихревых линийвозникаетвинтовоедвижение.
Если через каждую точку замкнутого контура по аналогии с трубкой тока провести вихревую линию, то совокупность таких линий образует вихревую трубчатую поверхность – вихревую трубку.
Гидрогазодинамика. Учеб. пособие |
85 |

4.КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
4.6.Движение жидкости в локальном объеме. Первая кинематическая теорема Коши ( Гельмгольца
Вдеформационном движении три одноименные частные производные
V1 |
, |
V |
V |
|
|
|
|
|
|
|
|
2 |
3 |
|
|
|
|
|
|
|
|
x1 |
x2 , |
x3 |
в функции S (4.28) характеризуют скорость изменения вели- |
|||||||
чины единичного объема. |
|
|
|
|
|
|
||||
|
|
Сумма |
|
|
|
|
|
|
|
|
|
|
|
|
V1 |
|
V2 |
|
V3 |
divV |
(4.30) |
|
|
|
|
x |
|
x |
|
x |
|
|
|
|
|
|
1 |
|
2 |
|
3 |
|
|
называется дивергенцией (расхождением) вектора скорости. Равенство divV 0 является условием несжимаемости жидкости при const . С тече-
нием времени в этом случае изменяется только форма выделенного объема. Оставшиеся слагаемые в правой части (4.28) характеризуют скошение (сдвиг) прямых координатных углов.
В гидромеханике различают движение без вращения элементов (потенциальное) и движение с их вращением (вихревое). В последнем случае из теоремы Гельмгольца легко видеть, что вихри перемещаются вместе с жидкостью со скоростью поступательного движения. С этим явлением можно встретиться, наблюдая за кольцами табачного дыма или дыма, выходящего из печной трубы: завихренность, видимая из-за присутствия в потоке мелких частиц продуктов сгорания, движется вместе с потоком нагретого воздуха.
Пример. Какие элементы характеризуют поступательное, вращательное и деформационное движение жидкой частицы в виде параллелепипеда, скорость точки С которой определяется в виде
V1C V1 S11dx1 S13dx3 S12dx2 2dx3 3dx2 ,
где
|
|
V |
|
S13 |
|
1 |
|
V1 |
|
V3 |
|
|
S |
|
|
1 |
|
V |
|
V |
|
|
|||
S |
|
1 ; |
|
|
|
|
|
; |
|
|
|
|
|
2 |
|
1 |
|
; |
|||||||
|
|
|
|
|
|
|
|||||||||||||||||||
11 |
|
x1 |
|
|
|
|
2 x3 |
|
x1 |
|
12 |
|
2 |
|
x1 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|||||||||||
|
|
|
|
1 |
|
V1 |
|
; |
|
1 |
V |
|
V |
|
. |
|
|
|
|||||||
|
|
2 |
|
V3 |
|
|
|
2 |
|
1 |
|
|
|
||||||||||||
|
|
|
2 |
|
x3 |
|
|
|
3 |
|
2 |
x |
|
x |
|
|
|
|
|
||||||
|
|
|
|
|
|
x1 |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
||
Деформационное движение жидкой частицы складывается из линейной деформации, характеризуемой соответствующими коэффициентами
S11 V1 / x1 ; S22 V2 / x2 ; S33 V3 / x3 ,
и угловой деформации, определяемой величинами
Гидрогазодинамика. Учеб. пособие |
86 |

4.КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
4.6.Движение жидкости в локальном объеме. Первая кинематическая теорема Коши ( Гельмгольца
S |
|
|
1 |
|
V3 |
|
V2 |
|
S |
|
|
1 |
|
V |
|
V |
|
S |
|
1 |
|
V2 |
|
V1 |
|
|||
|
2 |
|
x |
|
x |
; |
|
2 |
|
3 |
x |
1 |
; |
2 |
|
x |
x |
|
, |
|||||||||
|
23 |
|
|
2 |
|
|
|
31 |
|
|
x |
|
3 |
|
12 |
|
|
|
2 |
|
||||||||
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|||
т. е. полускоростями скашивания углов.
Поступательное движение жидкой частицы характеризуется скоростью V1, вращательное – величинами 2 dx3 и 3dx2 , деформационное – S11dx1 ,
S13dx3 и S12dx2 .
Пример. Определить скорость относительного кубического расширения в потоке газа, проекции скорости которого заданы уравнениями
V1 |
cx1 |
|
|
, V2 |
cx2 |
|
|
, V 0 |
, |
||
|
|
|
|
||||||||
|
x2 |
x2 |
|
x2 |
x2 |
3 |
|
||||
|
1 |
2 |
|
|
|
1 |
2 |
|
|
|
|
где плотность газа; с векторная константа.
Относительная скорость кубического расширения частицы жидкости с элементарным объемом dx1dx2dx3 определяется дивергенцией скорости:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V |
|
V |
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
divV |
x1 |
|
x |
2 |
|
3 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Исследуемый поток плоский V3 |
0 |
и установившийся, |
следователь- |
||||||||||||||||||||||||||||||||||||||||||
но, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V |
|
|
V |
|
|
|
c |
|
x |
2 |
|
x2 |
|
|
cx |
|
|
|
|
|
|
|
|
|
1 |
|
|
c |
|
|
x2 |
x2 |
|
||||||||||
divV |
|
|
1 |
|
|
|
2 |
|
|
|
|
2 |
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
x1 |
|
|
x2 |
|
|
x2 |
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
x2 |
2 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
x1 |
x2 x1 |
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
||
|
|
|
cx |
2 |
|
|
|
|
|
|
1 |
|
|
|
|
c |
|
|
x |
|
|
|
|
|
|
1 |
|
x |
|
|
|
|
1 |
. |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
x2 |
x2 |
x |
|
|
|
|
x2 x2 |
|
|
|
|
|
|
|
|
x |
|
|
||||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
1 x |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Пример. В двухмерном плоском потоке жидкости находится бесконечно малая частица в форме круга, уравнение которого
x12 x22 r 2 .
Какой будет форма этой частицы и как изменится ее площадь после деформации, если деформация линейная и происходит вдоль осей Ox1 и
Ox2 , являющихся главными осями деформаций?
Обозначим через x1 , x2 координаты, которые будет иметь точка A частицы через бесконечно малый промежуток времени dt . Поскольку Ox1 и
Гидрогазодинамика. Учеб. пособие |
87 |
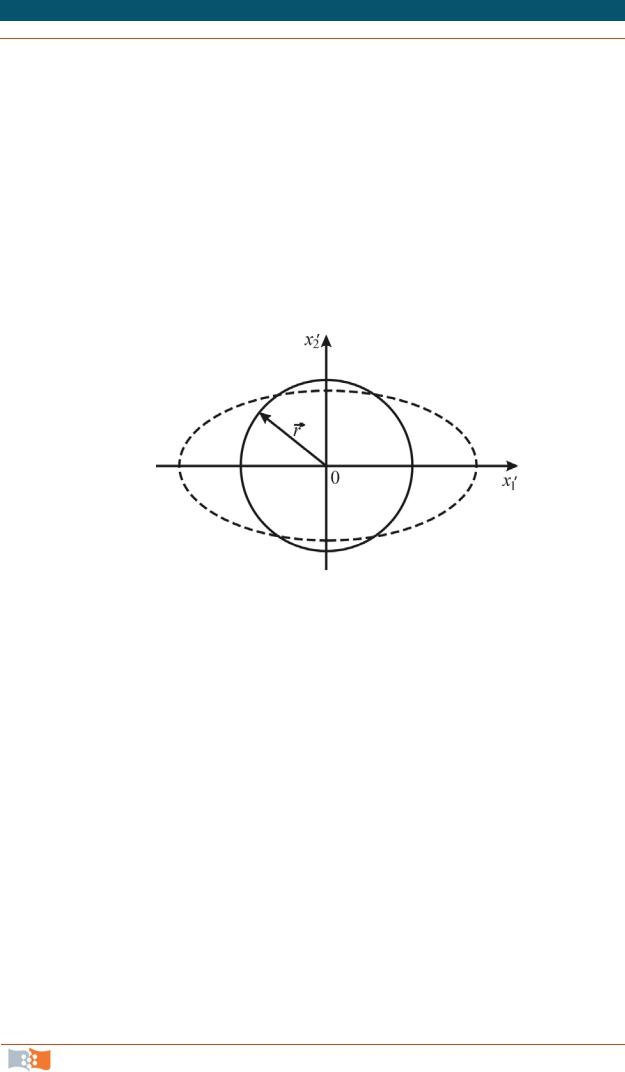
4.КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
4.6.Движение жидкости в локальном объеме. Первая кинематическая теорема Коши ( Гельмгольца
Ox2 являются главными осями, то вдоль них имеют место только линейные деформации и, следовательно,
|
|
x1 |
x1 |
|
|
V1 |
|
x1 |
dt , |
|
|
|
|||
|
|
x |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
x2 |
x2 |
|
V2 |
x2 dt . |
|
|
|
||||||
|
|
|
|
|
|||||||||||
Отсюда |
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
|
|
|
|
; x |
|
|
|
x1 |
|
|
. |
|||
|
V1 |
|
|
|
|
|
|||||||||
|
|
|
|
|
V |
|
|||||||||
|
1 |
dt |
2 |
|
|
1 |
dt |
||||||||
|
x |
|
|
|
|
x |
2 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 4.25
Подставляя значения x1, x2 в уравнение заданной бесконечно малой частицы в форме круга, найдем
|
|
|
x1 2 |
|
|
|
|
|
|
x2 2 |
|
|
1. |
||
|
|
|
|
V |
|
2 |
|
|
|
|
V |
|
2 |
||
|
2 |
|
|
|
|
2 |
|
|
|
||||||
r |
|
|
|
1 |
|
|
|
r |
|
|
|
1 |
|
|
|
|
1 |
x |
dt |
|
|
|
1 |
x |
dt |
|
|
||||
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
Это уравнение является уравнением эллипса с полуосями
|
|
V1 |
|
|
|
V2 |
|
|
|
|
|
|
|
|
|||
r 1 |
x |
dt |
и r 1 |
x |
2 |
dt . |
||
|
|
1 |
|
|
|
|
|
|
Таким образом, бесконечно малая частица в форме круга, деформируясь, обращается в бесконечно малый эллипс, оси которого направлены по главным осям деформации (см. рис. 4.25).
Гидрогазодинамика. Учеб. пособие |
88 |
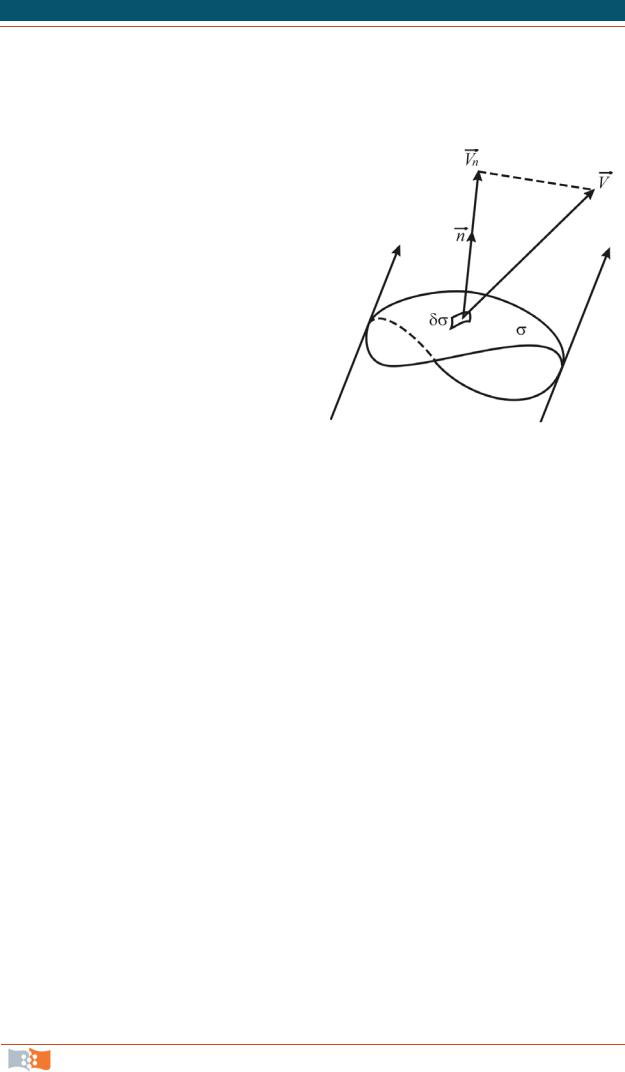
4. КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
4.7. Уравнениесекундногорасхода
Рассмотрим простейший случай секундного расхода жидкости Q, протекающей сквозь поверхность σ, пересекающую трубку тока, определяемого как поток
вектора скорости V . Выделим на поверхности σ элементарную площадку δσ и отметим направление нормали n к этой площадке (рис. 4.26). Сквозь поверхность σ жидкость протекает с какой-то
скоростью V . Известно, что расход дает только нормальная составляющая скорости Vn. Тогда расход через элементарную площадку δσ составит
Рис. 4.26
Q Vn .
Секундный расход есть поверхностный интеграл
QVn d V cos V n d .
При условии несжимаемой жидкости
Q Vn const
(4.31)
(4.32)
(4.33)
вдоль данной трубки тока.
Используя уравнение (4.32), получим практическое выражение для определения объемной Q (массовой m ) производительности (расхода) через
любое произвольное сечение потока:
Q VS , или m VS . |
(4.34) |
Здесь S площадь проходного сечения, V осредненная скорость потока в этом сечении.
Гидрогазодинамика. Учеб. пособие |
89 |
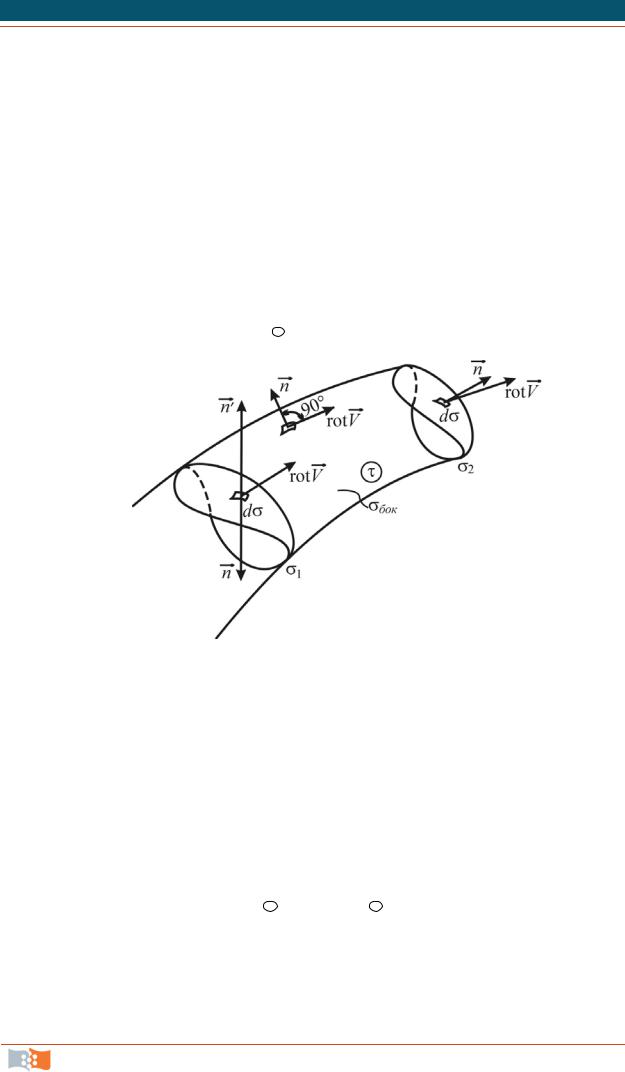
4.КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
4.8.ВтораякинематическаятеоремаГельмгольца
Эта теорема гласит: поток вектора вихря скорости сквозь произвольно проведенное сечение вихревой трубки одинаков в данный момент времени вдоль всей трубки, т. е. подобно тому как поток вектора скорости характеризует трубку тока, так поток вектора вихря характеризует вихревую трубку.
Для доказательства этой теоремы рассмотрим объем вихревой трубки τ (рис. 4.27), ограниченный боковой поверхностью σбок и произвольными сечениями σ1 и σ2, запишем известное преобразование Остроградского Гаусса для вектора Q rot V :
n d d . |
(4.35) |
|
|
|
|
Рис. 4.27
Разобьем поверхностный интеграл на три части, соответствующие по-
верхностям 1 , 2 и V n S t |
n V S t, . Так как на боковой поверх- |
|
ности n бок , поверхностный интеграл по бок равен нулю, |
а следовательно, |
|
тождественно равен нулю и объемный интеграл: |
|
|
Ω div rot V V 0. |
(4.36) |
|
Тогда будем иметь |
|
|
rotn Vd rotnVd 0. |
(4.37) |
|
1 |
2 |
|
Для единообразного определения потока вектора сквозь сечение трубки в направлении векторных линий заменим направление нормали в сечении 1
противоположным n . Тогда изменится знак первого слагаемого (4.37), получим
Гидрогазодинамика. Учеб. пособие |
90 |

4.КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
4.8.Вторая кинематическая теорема Гельмгольца
S 1 rotV S 2 rotV , |
(4.38) |
где S 1 и S 2 площади сечений 1 и 2 , что и доказывает вторую тео-
рему Гельмгольца.
Величина потока вихря вдоль вихревой трубки называется интенсивностью вихревой трубки i и характеризует трубку в целом. Итак,
i S rotV rotnVd . |
(4.39) |
|
|
Согласно второй теореме Гельмгольца вихревые трубки не могут заканчиваться и начинаться в жидкости. Если бы вихревая трубка начиналась (заканчивалась) нулевым сечением ( S 0 ), в этом сечении угловые скорости
вращения частиц жидкости возросли бы до бесконечности.
Вихревые трубки могут образовывать замкнутые кольца (например колечки дыма), могут начинаться на твердых стенках или свободных поверхностях (водовороты, смерчи, циклоны и антициклоны, воронки, образующиеся при вытекании воды из резервуара через отверстие, расположенное на дне, и
т. д.).
В практической деятельности знание интенсивности вихревой трубки крайне важно. Вихревой трубкой, например, является крыло самолета или судна на подводных крыльях. Измерениям впрямую i не поддается, ее вычисляют аналитическим путем.
4.9. ТеоремаСтокса
Более удобной мерой вихревого движения является циркуляция скорости Г, обычно используемая в гидромеханических расчетах. Циркуляция Г определяется поступательной скоростью жидкости.
Рассмотрим отрезок AB (рис. 4.28) некоторой кривой C , проведенной
в поле скоростей V , где dr – направленный элемент дуги этой кривой. Криволинейный интеграл
B |
|
dr |
B |
|
dr |
|
AB V |
VdScos V |
|
||||
A |
|
|
A |
|
|
(4.40) |
B |
|
B |
|
|
|
|
Vcos dS |
V1dx1 |
V2 dx2 V3dx3 |
|
|||
A |
|
A |
|
|
|
|
называется циркуляцией скорости по контуру С на участке АВ и явля-
ется скалярной величиной.
Из (4.40) следует, что циркуляция |
скорости представляет собой «рабо- |
|
ту» вектора V по замкнутому контуру |
C на участке |
AB . Если контур C |
|
|
|
Гидрогазодинамика. Учеб. пособие |
91 |
|
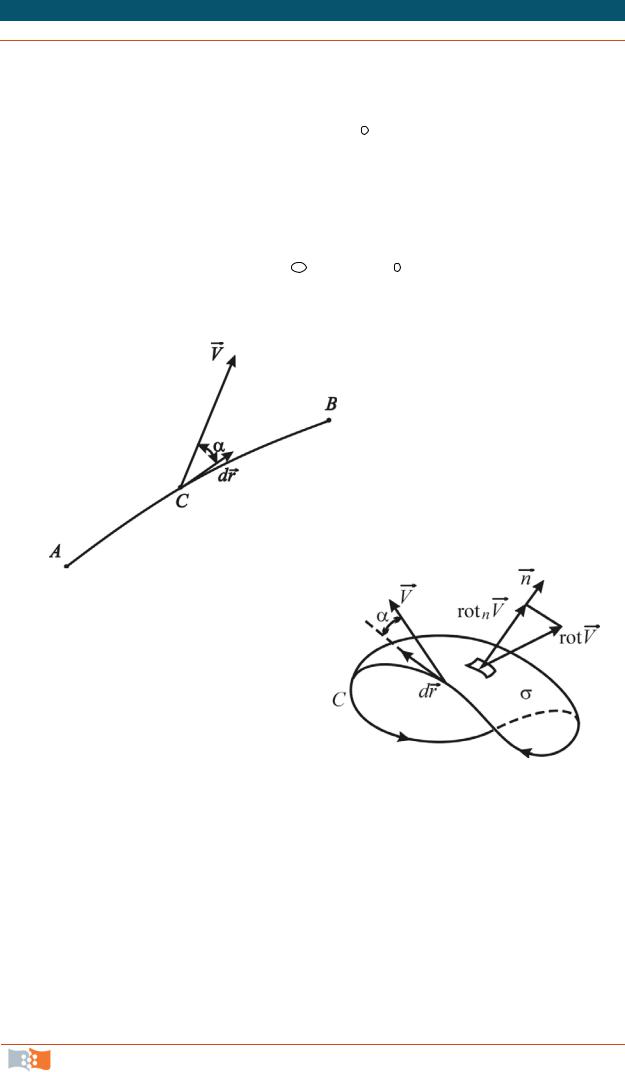
4.КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
4.9.Теорема Стокса
замкнут, то циркуляция вектора (в данном случае вектора скорости) выражается контурным интегралом
ñ V dr. |
(4.41) |
ñ |
|
Если в поле вихря провести произвольное сечение с опоясывающим контуром C (контур сам себя не пересекает), то (рис. 4.29)
rotnVd V dr. |
(4.42) |
|
|
c |
|
Рис. 4.28 |
Рис. 4.29 |
Теорема Стокса утверждает, что циркуляция скорости по замкнутому контуру, расположенному на поверхности вихревой трубки и один раз ее опоясывающему, равна интенсивности вихревой трубки. Теорема Стокса сводит количественное определение интенсивности вихревой трубки к вычислению циркуляции скорости, непосредственное измерение которой на практике не представляет затруднений.
Гидрогазодинамика. Учеб. пособие |
92 |

4.КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
4.9.Теорема Стокса
Если замкнутый контур охватывает несколько вихревых трубок, циркуляция по нему представляет собой алгебраическую сумму циркуляций по всем вихревым трубкам.
Когда циркуляция скорости по любому замкнутому контуру, произвольно проведенному в движущейся жидкости, равна нулю, можно судить об отсутствии вихревых трубок. Такое движение называется безвихревым и характеризуется равенством rotV 0 во всей области течения.
Гидрогазодинамика. Учеб. пособие |
93 |

4.КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
4.10.Третьякинематическаятеорема(Кельвина)
Теорема Кельвина заключается в том, что индивидуальная производная по времени от циркуляции скорости равна циркуляции ускорения по тому же контуру. Рассмотрим движение жидкого контура, состоящего из одних и тех же частиц жидкости. По определению
d |
|
d |
|
|
|
|
|
|
V |
r |
V r, |
(4.43) |
|||
dt |
dt |
||||||
|
c |
|
c |
|
где r ориентированный элемент контура интегрирования.
Если контур C неподвижен, неизменяем, тогда выражение (4.43) верно без доказательства. В данном же случае контур изменяется (изменяется r ). Проведем соответствующее доказательство теоремы Кельвина для движущегося контура. Для этого воспользуемся основными правилами определения производной от сложных функций. Тогда
d |
V r |
d |
V r dV |
r V |
d |
r . |
|
|
|
|
|||||
dt |
c |
c dt |
c dt |
c |
dt |
|
|
Рассмотрим второе слагаемое в правой части (4.44):
|
|
d |
|
|
dr |
|
|
||
V |
|
|
r |
V |
|
V |
V . |
||
dt |
|||||||||
ñ |
|
|
c |
dt |
c |
|
|||
(4.44)
(4.45)
Из математики известно, что |
|
|
|
x |
2 |
|
есть бесконечно малая вели- |
||||
|
|
|
|
|
|||||||
|
|
|
|
||||||||
x x |
|
|
|
|
|||||||
|
|
|
|
|
|
2 |
|
|
|||
чина, следовательно, |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
V |
V |
|
V |
|
|
|
0 |
, |
||
|
|
|
|
|
|||||||
|
|
|
2 |
|
|||||||
c |
|
|
|
c |
|
|
|
|
|||
и таким образом (4.43) доказано для движущегося жидкого контура. Из теоремы Кельвина следует, что Г по замкнутому контуру (или в об-
щем случае интенсивность вихревой трубки) изменяется со временем и зависит от распределения ускорения в жидкости, т. е. от распределения приложенных к жидкости сил.
Гидрогазодинамика. Учеб. пособие |
94 |

4.КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
4.11.Четвертаякинематическаятеорема(Лагранжа)
Предположим, что в некоторый начальный момент времени во всех точках жидкости отсутствует завихренность rotV 0 , т. е. элементарные
жидкие объемы движутся без вращения, совершая лишь поступательные и круговое движения. Тогда на основании теоремы Стокса циркуляция по произвольному жидкому контуру будет равна нулю. На основании теоремы Кельвина и в любой другой момент времени циркуляция будет равна нулю.
Отсюда следует теорема Лагранжа: если во всей движущейся жидкости
вихрь скорости в некоторый начальный момент был равен нулю, то движениеостанетсябезвихревымивлюбойдругойпоследующиймоментвремени.
Аналогично утверждение о том, что если движение идеальной жидкости в начальныймоментвременибыловихревым, тооносохранитсяивпоследующем.
В действительности наблюдается образование и исчезновение вихревых движений, что вызвано внутренним трением в жидкости.
4.12. Методывизуализацииполятечения
Методы непосредственной визуализации (наблюдения) позволяют определить такие характеристики течения, как траекторию, или путь, проходимый отдельной частицей жидкости, линию тока, а также поле скоростей и давлений и даже величину касательных напряжений в жидкости.
Эти методы подразделяются на две группы: оптические (особенно эффективны для сжимаемой среды и при больших числах Маха); неоптические (очень эффективны при моделировании в гидродинамических трубах процессов вдува, отсоса, течения во внутренних каналах). Для визуализации нестационарных быстропротекающих процессов, например, движения вихрей или развития каверн, используется фотографирование с короткой экспозицией до
10 5 –10 7 с.
Неоптические методы
Наиболее удобным методом визуализации плоского и пространственного течения в гидротрубах и гидроканалах является метод пузырьков, используемый для измерения скорости в пограничном слое. Перпендикулярно поверхности стенки трубы устанавливается платиновая проволока – электрод, а второй электрод – в воде. При подаче импульса напряжения в результате электролиза на проволоке появляется ряд небольших пузырьков, который «метит» нужный элемент. При движении вниз по потоку ряд пузырьков деформируется в соответствии с формой профиля скорости. Для получения водородных пузырьков напряжение источника должно быть 10–250 В.
Применение дыма используется в аэродинамике.
Гидрогазодинамика. Учеб. пособие |
95 |

4.КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
4.12.Методы визуализации поля течения
Применение красителей – подача их через специальные отверстия в модели – позволяет наблюдать течения у стенки. Для визуализации всего поля течения около модели используют насадок, помещаемый в различные точки потока. При этом необходимо соблюдать равенство скорости красителя и потока, удельного веса красителя и рабочей жидкости, чтобы исключить влияние подъемной силы. Краситель также должен эффективно поглощать свет. Используемые материалы: пинакрептол, эозин, белое снятое и подкрашенное молоко, нитрозин и др.
Метод трассирующих частиц применяют для визуализации плоского течения несжимаемой жидкости. Материалы: алюминиевая пудра (размер частиц 20–400 мкм), споры плауна (28–50 мкм), чешуя слюды, стеклянные или пластмассовые шарики.
Метод нитей. Нити из шелка, нейлона, шерсти длиной не более 19 мм закрепляются на поверхности модели в аэродинамической трубе или на поверхности обтекаемого профиля (тела) в свободном полете.
Метод масляной пленки и масляных капель используется в гидродина-
мических (кавитационных) трубах. Поверхность профиля покрывается слоем смазочного масла или наносятся капли, которые движутся под действием сил поверхностного трения. При этом в зоне ламинарного течения наблюдается пленка (скопление масла) в зоне отрыва и почти полное отсутствие его в зоне турбулентного течения.
Метод электрохемолюминесценции. В потоке хемолюминесцентного раствора помещают электроды. При подаче напряжения у поверхности анода возникает голубое свечение. Аноду придается форма модели, катоду – любая форма. Свечение занимает область, примерно равную толщине пограничного слоя.
Оптические методы шлирен-метод, теневой, интерферометрический, голография и др.
Оптические методы основаны на изменении освещенности, создаваемой параллельным потоком света, проходящим через среду разной оптической плотности. Плотность среды меняется в зависимости от изменения гидродинамических характеристик потока при обтекании им модели какоголибо тела. При этом на экране наблюдаются более светлые и темные области, появление которых вызвано отклонением падающих лучей.
Первые три метода используются для визуализации плоских и осесимметричных потоков, а для наблюдений за пространственными течениями используется лазерная голография. Голограмма представляет собой картину интерференции, образованную при наложении двух волн от лазерного источника света. Голограмма – очень эффективный метод регистрации нестационарных потоков.
Гидрогазодинамика. Учеб. пособие |
96 |
