Методические указания к практическим занятиям по математике 4 семестр

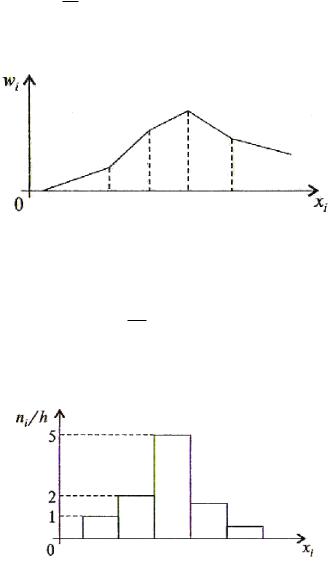
181

где n x число вариант, меньших x ; n объем выборки.

Полигон и гистограмма

Графически статистическое распределение может быть представлено в виде полигона, гистограммы или графика накопленных частот.

Полигоном частот называют ломаную, отрезки которой соединяют

в случае дискретного распределения.

Гистограммой частот называется ступенчатая фигура, состоящая из прямоугольников, основанием которых служат частичные интервалы

длины h , а высоты равны ni . Площадь гистограммы частот равна сумме

h

всех частот, т.е. объему выборки.

Рис. 15.1

Для построения гистограммы относительных частот за высоту

прямоугольников берут величину wi (рис. 15.2). Площадь гистограммы

h

относительных частот равна сумме всех относительных частот, т.е. единице.

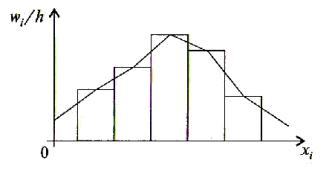
Рис. 15.2

182

Рис. 15.3

Гистограммы обычно служат для изображения выборки в случае непрерывного распределения. Если на гистограмме частот соединить середины верхних сторон прямоугольников, то полученная ломаная образует полигон частот. Аналогично получается полигон относительных частот из гистограммы относительных частот (рис. 15.3).

При построении гистограммы в реальных исследованиях следует понимать, что формула Стерджеса для числа интервалов разбиения k дает лишь рекомендацию, а не строгое правило. Если взять слишком маленькое число k , то гистограмма получится грубой, плохо отражающей свойства распределения. При слишком больших k гистограмма становится «колючей», имеет игольчатый вид, и может распасться на отдельные «иглы» и пустые интервалы. Оптимальное значение k в общем случае неизвестно – оно зависит как от типа распределения, так и от конкретной выборки.

Графиком накопленных частот называется фигура, строящаяся аналогично гистограмме относительных частот, с тем различием, что для расчета высот прямоугольников вместо относительных частот берутся накопленные относительные частоты, т.е. величины

j 1

Эти величины неубывают и, таким образом, график накопленных частот имеет вид ступенчатой «лестницы». График эмпирической функции распределения проходит через правые верхние углы прямоугольников, то есть через точки вида (ci , wic ) . График накопленных частот и эмпирическая функция распределения на практике используются для приближения теоретической функции распределения.

183

Примеры решения задач

1. Построить эмпирическую функцию по данному распределению выборки:

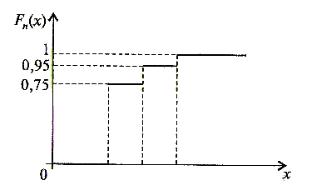
Эмпирическая функция распределения имеет вид (рис. 15.4):

0, есл и x 2;

0 .7 5, есл и 2 x 3;

Fn ( x ) 0 .9 5, есл и 3 x 5;

1, есл и x 5 .

184

Рис. 15.4

2. По данным выборки составить дискретное статистическое распределение: 1, 10, 15, 13, 9, 13, 7, 6, 1, 2, 10, 9, 15, 1, 7, 7, 7, 8, 1, 13.

Решение. Объем выборки n 20 . Построим дискретный вариационный ряд, для этого надо расположить все значения выборки в возрастающем порядке. Получим

1, 1, 1, 1, 2, 6, 7, 7, 7, 7, 8, 9, 9, 10, 10, 13, 13, 13, 15, 15.

Теперь, по вариационному ряду, составим таблицу. В первой строке записываем различные варианты ряда, во второй строке – частоты соответствующих вариант, т.е. число повторений каждой варианты.

получиться равной числу n , т.е. объему выборки. Проверим:

4 1 1 4 1 2 2 3 2 20 .

3. По данным выборки объема n 60 построить статистическое распределение.

1; 2,5; 1,5; 4; 6; 6,1; 3,7; 6,5; 2,5; 8,1; 7,8; 9,1; 5,1; 10; 13,4; 8,2; 4; 9,4; 11; 14,8; 13,2; 11,7; 15; 14,8; 12,8; 9,7; 13; 14; 3,4; 13,4; 8,4; 9,4; 9,1; 10,5; 4,8; 5; 1,3; 2,8; 8,6; 7; 14; 15; 7,3; 10; 12,7; 1,7; 5,6; 7,5; 8,9; 11,3; 13,7; 3; 6,3; 4; 3,2; 6,7; 15; 1,2; 7,9; 9,5.

185

Решение. Так как объем выборки достаточно велик и выборка содержит большое количество различных элементов, то данные выборки лучше сгруппировать. Найдем сначала крайние элементы ряда: xm in 1, xm ax 1 5 . Значит отрезок [1; 15] надо разбить на k интервалов

одинаковой длины. Чтобы найти оптимальное число интервалов разбиения, воспользуемся формулой Стерджеса (15.1)

k 1 lo g 2 n 1 log 2 60 7 .

То есть отрезок [1, 15] разбиваем на 7 интервалов. Длина этих интервалов одинакова и вычисляется по формуле (15.2):

h xm ax xm in 15 1 2 .

Получим следующие интервалы:

[1; 3), [3; 5), [5; 7), [7; 9), [9; 11), [11; 13), [13; 15].

Теперь надо найти частоты соответствующих интервалов. Частота каждого интервала это количество вариант, вошедших в этот интервал. Например, первый интервал [1; 3) попадают элементы 1; 2,5; 1,5; 2,5; 1,3;

2,8; 1,7; 1,2. Всего 8 элементов, значит, частота интервала [1; 3) равна 8. Проводя аналогичные рассуждения, получим следующую таблицу:

Эта таблица задает статистическое распределение исходной выборки.

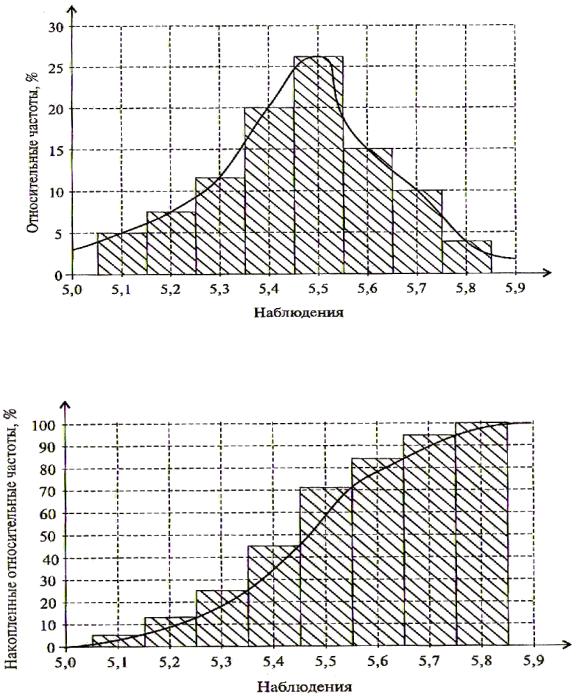
4. Анализируется выборка из 100 малых предприятий региона. Цель обследования – измерение коэффициента соотношения заемных и собственных средств xi на каждом i ом предприятии. Результаты

анализа представлены в табл. 15.1. Требуется построить гистограмму и график накопленных частот.

186

Решение. Построим сгруппированный ряд наблюдений (табл. 15.2).

k 1 log 2 100 7, 62; k 8 .

Отсюда получаем, что длина интервала (15.2)

Таблица 15.1

Таблица 15.2

187

Рис. 15.5

Рис. 15.6

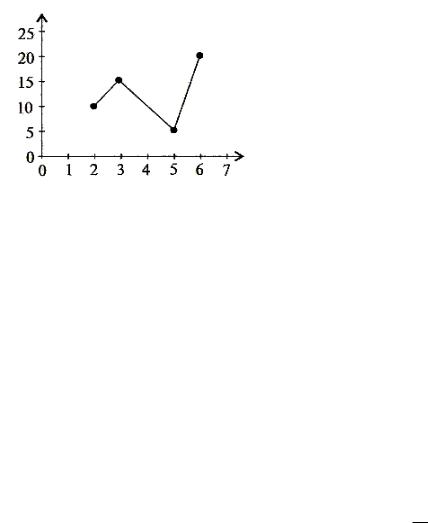
5. Построить полигон частот по данному распределению выборки:

xi , ni . Полигон частот имеет вид:

188

Рис. 15.7

6. Построить гистограмму частот по данному распределению выборки:

Решение. Сначала найдем плотности частот, то есть величины ni .

h

Для данного примера h 5 . Таким образом, получаем

Отложим на оси абсцисс интервалы длиной h 5 каждый, а затем проведем над ними отрезки, параллельные оси x , на расстояниях от нее,

равных соответствующим значениям плотности частоты (ось ординат), т.е. гистограмма частот состоит из прямоугольников, ширина каждого прямоугольника равна длине интервала h 5 , а высота равна плотности соответствующей частоты (рис. 15.8).

189

Рис. 15.8

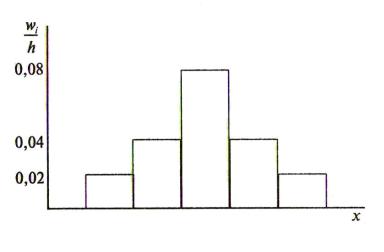
7. Построить гистограмму относительных частот и график накопленных частот по данному распределению выборки:

Решение. Найдем относительные частоты и плотности относительных частот:

190

Построим на оси абсцисс частичные интервалы h 5 , затем проведем параллельно им отрезки, отстоящие от оси x на соответствующие значения плотности относительной частоты:

Рис. 15.9

График накопленных частот строится аналогично гистограмме относительных частот, но вместо значений плотностей относительных частот, на оси ординат откладываются значения плотностей накопленных частот, т.е. мы строим прямоугольники, ширина которых равна h 5 , а высоты прямоугольников равны плотностям накопленных частот. Так как накопленные частоты возрастают с увеличением индекса, то и фигура должна получиться возрастающей.

Задачи для самостоятельного решения

1. Данные выборки приведены в таблице. Построить полигон частот. а)