
lect_14
.pdfТопологическая сортировка. Сильно связные компоненты. Минимальные остовные деревья
План лекции
1.Топологическая сортировка
2.Сильно связные компоненты.
3.Минимальные остовные деревья (понятие).
4.Построение минимального остовного дерева.
5.Правило для распознавания безопасных ребер.
6.Алгоритм Крускала.
7.Алгоритм Примы.
Топологическая сортировка
Рассмотрим, каким образом можно использовать поиск в глубину для топологической сортировки ориентированного ациклического графа (directed acyclic graph, для которого иногда используется аббревиатура "dag").
Топологическая сортировка (topological sort) ориентированного ациклического графа G = (V, Е) представляет собой такое линейное упорядочение всех его вершин, что если граф G содержит ребро (u,v), то u при таком упорядочении располагается до v (если граф не является ацикличным, такая сортировка невозможна).
Топологическую сортировку графа можно рассматривать как такое упорядочение его вершин вдоль горизонтальной линии, что все ребра направлены слева направо. Ориентированные ациклические графы используются во многих приложениях для указания последовательности событий. На рисунке приведен пример графа, построенного профессором Рассеянным для утреннего одевания. Некоторые вещи надо обязательно одевать раньше других, например, сначала носки, а затем туфли. Другие вещи могут быть одеты в произвольном порядке (например, носки и рубашка). Ребро (u, v) в ориентированном ациклическом графе на рисунке показывает, что вещь u должна быть одета раньше вещи v. Топологическая сортировка этого графа дает нам порядок одевания. Ниже показан отсортированный риентированный ациклический граф, вершины которого расположены вдоль горизонтальной линии так, что все ребра направлены слева направо.
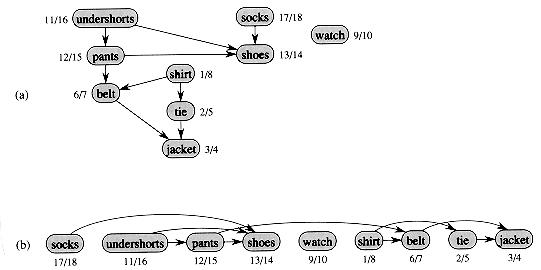
Вот простой алгоритм топологической сортировки ориентированного ациклического графа:
TopologicalJSort(G)
1 Вызов DFS(G) для вычисления времени завершения f[v] для каждой вершины v
2 По завершении работы над вершиной внести ее в начало связанного списка 3 return Связанный список вершин
На рисунке видно, что топологически отсортированные вершины располагаются в порядке убывания времени завершения.
Мы можем выполнить топологическую сортировку за время в (V + Е), поскольку поиск в глубину выполняется именно за это время, а вставка каждой из |V| вершин в начало связанного списка занимает время О A).
Докажем корректность этого алгоритма с использованием следующей ключевой леммы, характеризующей ориентированный ациклический граф.
Лемма Ориентированный граф G является ациклическим тогда и только тогда, когда поиск в глубину в G не находит в нем обратных ребер.
Доказательство. =>: Предположим, что имеется обратное ребро (u,v). Тогда вершина v является предком u в лесу поиска в глубину. Таким образом, в графе G имеется путь из v в u, и ребро (и, v) завершает цикл.
<=: Предположим, что граф G содержит цикл с. Покажем, что поиск в глубину обнаружит обратное ребро. Пусть v — первая вершина, открытая в с, и пусть (u, v) — предыдущее ребро в с. В момент времени d [v] вершины с образуют путь из белых вершин от v к u. В соответствии с теоремой о белом
пути, вершина u становится потомком v в лесу поиска в глубину. Следовательно, (u, v) — обратное ребро.
Теорема . Процедура Topological_Sort(G) выполняет топологическую сортировку ориентированного ациклического графа G.
Доказательство. Предположим, что над данным ориентированным ациклическим графом G = (V, Е) выполняется процедура DFS, которая вычисляет время завершения его вершин. Достаточно показать, что если для
произвольной пары разных вершин u,v V в графе G имеется ребро от u к v, то f[v] < f[u].
Рассмотрим произвольное ребро (u, v), исследуемое процедурой DFS(G). При исследовании вершина v не может быть серой, поскольку тогда v была бы предком u и (u, v) представляло бы собой обратное ребро, что противоречит лемме.Следовательно, вершина v должна быть белой либо черной. Если вершина v — белая, то она становится потомком u, так что f[v]<f [и]. Если v — черная, значит, работа с ней уже завершена и значение f[v] уже установлено. Поскольку мы все еще работаем с вершиной u значение f[и] еще не определено, так что, когда это будет сделано, будет выполняться неравенство f[v]<f [и]. Следовательно, для любого ребра (u, v) ориентированного ациклического графа выполняется условие f[v]<f [и], что и доказывает данную теорему.
Сильно связные компоненты
Сильно связный компонент ориентированного графа G = (V, Е) представляет собой максимальное множество вершин С V, такое что для каждой пары вершин u и v из С справедливо как u→ v, так и u→ v, т.е. вершины u и v достижимы друг из друга.
Наш алгоритм поиска сильно связных компонентов графа G = (V, Е) использует транспонирование графа G. Транспонированный граф определяется следующим образом: GT = (V, Ет), где Ет = {(u, v) : (v, u) Е}, т.е. Ет состоит из ребер G, направление которых изменено на обратное. Для представления с помощью списков смежности данного графа G, получить граф GT можно за время О (V + Е).
Интересно заметить, что графы G и GT имеют одни и те же сильно связные компоненты: u и v достижимы друг из друга в G тогда и только тогда, когда они достижимы друг из друга в GT. На рисунке б) показан граф, представляющий собой результат транспонирования графа на рисунке а) (сильно связные компоненты выделены штриховкой).
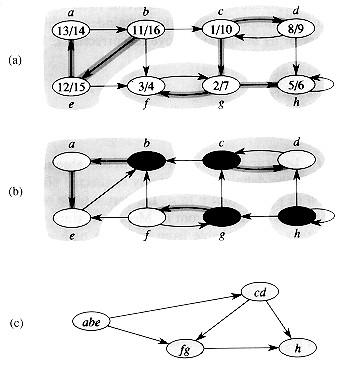
Далее приведен алгоритм, который за линейное время G (V + Е) находит сильно связные компоненты ориентированного графа G = (V, Е) благодаря двойному поиску в глубину, одному — в графе G, и второму — в графе GT.
Strongly_Connected_Components(G)
1 Вызов DFS(G) для вычисления времен завершения f[u] для каждой вершины u
2 Построение GT
3 Вызов DFS(GT), но в главном цикле процедуры DFS, вершины рассматриваются в порядке убывания значений f[u], вычисленных в строке 1.
4 Деревья леса поиска в глубину, полученного в строке 3 представляют собой сильно связные компоненты.
Идея, лежащая в основе этого алгоритма, опирается на ключевое свойство графа компонентов (component graph) Gscc = (Vscc, Escc), который определяется следующим образом. Предположим, что G имеет сильно связные компоненты С1, С2,..., Cк. Множество вершин Vscc = {v1, v2,..., vk} состоит из вершин vi для каждого сильно связного компонента Сi графа G. Если в G имеется ребро (x,y) для некоторых двух вершин х Ci и у Cj, то в
графе компонент имеется ребро (vi,vj) Escc. Другими словами, если сжать все ребра между смежными вершинами в каждом сильно связном компоненте графа G, мы получим граф GSCC (вершинами которого являются сильно связные компоненты графа G). На рисунке в) показан граф компонентов для графа, приведенного на рисунке а).
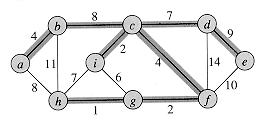
Ключевое свойство графа компонентов заключается в том, что он представляет собой ориентированный ациклический граф.
Минимальные остовные деревья
Пусть задан связный неориентированный граф G = (V,E) и для каждого ребра (u,v) E задан вес w(u,v). Мы хотим найти ациклическое подмножество T E, которое соединяет все вершины и чей общий вес
w(T) = Σ(u,v) Tw (u, v) – минимален. Поскольку множество T ациклическое и связывает все вершины, оно должно образовывать дерево, которое мы назовем остовным деревом (spanning tree) графа G (иногда используется термин "покрывающее дерево"). Задачу поиска дерева Т мы назовем задачей поиска минимального остовного дерева (minimum- spanning-tree problemI. На рисунке показан пример связного графа и его минимального остовного дерева. На ребрах указан их вес, а ребра минимального остовного дерева отдельно выделены цветом.
Мы рассмотрим два алгоритма решения задачи поиска минимального остовного дерева — алгоритм Крускала (Kruskal) и Прима (Prim). Каждый из них легко реализовать с помощью обычных бинарных пирамид, получив время работы О(ElgV). При использовании фибоначчиевых пирамид алгоритм Прима можно ускорить до О (Е + V lg V), что является весьма существенным ускорением при |V|«|E|.
Оба эти алгоритма — жадные. На каждом шаге алгоритма мы выбираем один из возможных вариантов. Жадная стратегия предполагает выбор варианта, наилучшего в данный момент. В общем случае такая стратегия не гарантирует глобально оптимального решения задачи, однако для задачи поиска минимального остовного дерева можно доказать, что определенные жадные стратегии дают нам остовное дерево минимального веса.
Построение минимального остовного дерева
Минимальное остовное дерево растет путем добавления к нему ребер по одному. Алгоритм работает с множеством ребер А, и инвариант цикла алгоритма выглядит следующим образом:
Перед каждой очередной итерацией А представляет собой подмножество некоторого минимального остовного дерева.
На каждом шаге алгоритма мы определяем ребро (u, v), которое можно добавить к А без нарушения этого инварианта, в том смысле, что А {(u,v)} также является подмножеством минимального остовного дерева. Мы назовем такое ребро безопасным (safe edge) для А, поскольку его можно добавить к А, не опасаясь нарушить инвариант.
Generic_MST(G, w) 1 A←0
2 while А не является минимальным остовным деревом
3 do Найти безопасное для А ребро (u, v)
4 A←A {(u,v)}
5 return A
Мы используем инвариант цикла следующим образом. Инициализация. После выполнения строки 1 множество А тривиально удовлетворяет инварианту цикла.
Сохранение. Цикл в строках 2-4 сохраняет инвариант путем добавления только безопасных ребер.
Завершение. Все ребра, добавленные в А, находятся в минимальном остовном дереве, так что множество А, возвращаемое в строке 5, должно быть минимальным остовным деревом.
Правило для распознавания безопасных ребер
Разрезом (cut) S, V — S) неориентированного графа
G = (V, Е) называется разбиение V, что проиллюстрировано на рисyнке (вершины в множестве S окрашены в черный цвет, а в множестве V — S — в белый). Мы говорим, что ребро (u, v) Е пересекает (crosses) разрез (S, У — S), если один из его концов оказывается в множестве S, а второй — в V — S. Разрез согласован (respect) с множеством А по ребрам, если ни одно ребро из А не пересекает разрез. Ребро, пересекающее разрез, является легким (light), если оно имеет минимальный вес среди всех ребер, пересекающих разрез. Заметим, что может быть несколько легких ребер одновременно. В общем случае мы говорим, что ребро является легким ребром, удовлетворяющим некоторому свойству, если оно имеет минимальный вес среди всех ребер, удовлетворяющих данному свойству.
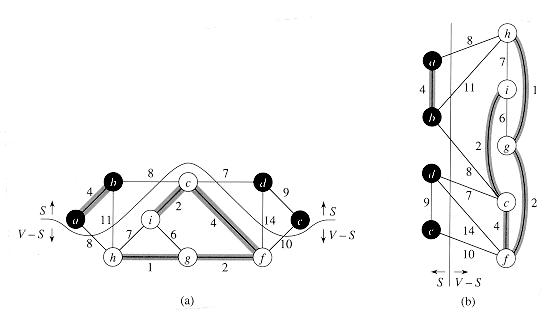
Два варианта представления разреза графа.
Пусть G = (У, Е) — связный неориентированный граф с действительной весовой функцией w, определенной на Е. Пусть А — подмножество Е, которое входит в некоторое минимальное остовное дерево G, (S, V — 5) — разрез G, согласованный с А по ребрам, а (u, v ) — легкое ребро, пересекающее разрез (S, V — 5). Тогда ребро (u, v) является безопасным для А. (утв.1)
Пусть Т — минимальное остовное дерево, которое включает А, и предположим, что Г не содержит ребро (u, v), поскольку в противном случае теорема доказана. Мы построим другое минимальное остовное дерево Т", которое включает A {(u, v)}, путем использования метода вырезания и вставки, показывая таким образом, что ребро (u, v) является безопасным для А. Ребро (u, v) образует цикл с ребрами на пути р от u к v в Т. Поскольку u и v находятся на разных сторонах разреза (S, V — S), на пути р имеется как минимум одно ребро из Т, которое пересекает разрез. Пусть таким ребром является ребро (x, y). Ребро (x, у) не входит в А, поскольку разрез согласован с А по ребрам. Так как (x, у) является единственным путем от u к v в Т, его удаление разбивает Т на два компонента. Добавление (u, v) восстанавливает разбиение, образуя новое остовное дерево T’ = Т — {(х, у)} U {(u, v)}.
Теперь мы покажем, что Т" — минимальное остовное дерево. Поскольку (u, v) — легкое ребро, пересекающее разбиение (S, V — S), и (x,у) также пересекает это разбиение, w (u, v) ≤ w (x, у). Следовательно,
w (T') =w(T)-w (x, у) + w (u, v) ≤ w (T).
Однако Т — минимальное остовное дерево, так что w (T) < w (T’). Следовательно, T’ также должно быть минимальным остовным деревом.
Остается показать, что (x, у) действительно безопасное ребро для А. Мы имеем A Т", поскольку A Т и (х,y) А Таким образом,
A È {(u,v)} Í и, поскольку Т’ — минимальное остовное дерево, ребро (u, v) безопасно для A.
Пусть G = (V, Е) — связный неориентированный граф с действительной весовой функцией w, определенной на Е. Пусть А — подмножество Е, которое входит в некоторое минимальное остовное дерево G, и пусть С = {Vc,Ec) — связный компонент (дерево) в лесу Ga = (V,А). Если (u, v) — легкое ребро, соединяющее С с некоторым другим компонентом в Ga, тo ребро (u,v) безопасно для А. (утв.2)
Доказательство. Разрез (Vс, V — Vc) согласован с A, и (u,v) — легкое ребро для данного разреза. Следовательно, ребро (u, v) безопасно для А.
Алгоритм Крускала
Алгоритм Крускала непосредственно основан на обобщенном алгоритме поиска минимального остовного дерева, приведенном выше. Он находит безопасное ребро для добавления в растущий лес путем поиска ребра (u, v) с минимальным весом среди всех ребер, соединяющих два дерева в лесу. Обозначим два дерева, соединяемые ребром (u, v), как С1 и С2. Поскольку (u, v) должно быть легким ребром, соединяющим С1 с некоторым другим деревом, из сказанного выше вытекает, что (u, v) — безопасное для С1 ребро. Алгоритм Крускала является жадным, поскольку на каждом шаге он добавляет к лесу ребро с минимально возможным весом.
MST_Kruskal(G, w) 1 А¬0
2 for (Для) каждой вершины v Î V[G]
3 do Make_Set(v)
4 Сортируем ребра из Е в неубывающем порядке их весов w 5 for (Для) каждого (u, v) Î Е (в порядке возрастания веса) 6 do if Find_Set(u) ¹ Find_Set(v)
7 then A ¬ AÈ{(u,v)}
8 UNlON(u, v)
9 return A
Операция Find_Set(u) возвращает представительный элемент множества, содержащего u. Таким образом, мы можем определить, принадлежат ли две вершины и и v одному и тому же дереву, проверяя равенство Find_Set(u) и Find_Set(v). Объединение деревьев выполняется при помощи процедуры Union.
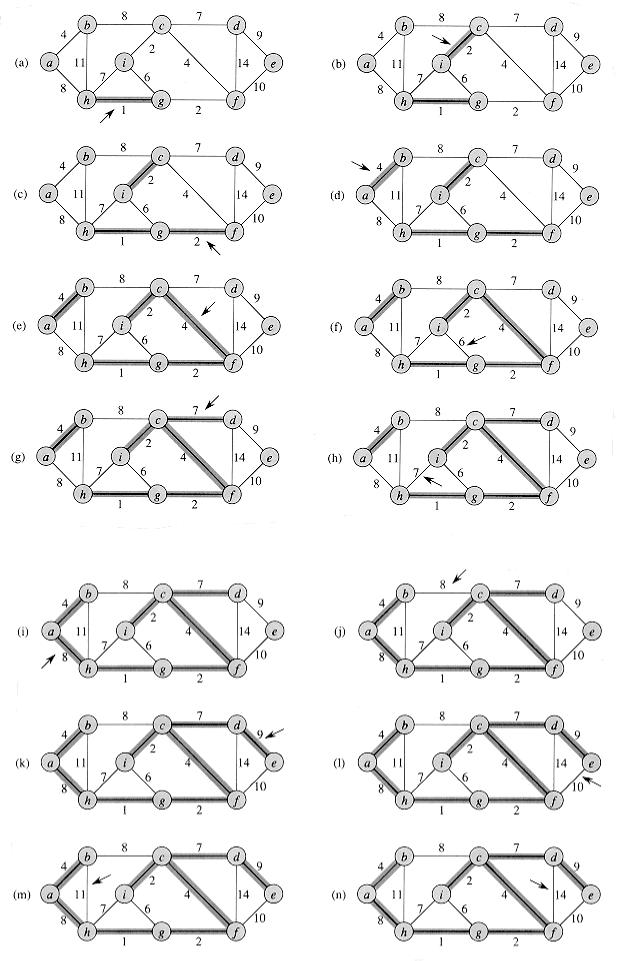
Время работы алгоритма Крускала для графа G = (V, Е) зависит от реализации структуры данных для непересекающихся множеств. Инициализация множества А в строке 1 занимает время О A), а время, необходимое для сортировки множества в строке 4, равно О (ElgE) (стоимость |V| операций Make_Set в цикле for в строках 2-3 мы учтем чуть позже). Цикл for в строках 5-8 выполняет О (Е) операций Find_Set и Union над лесом непересекающихся множеств. Вместе с |V| операциями Make_Set эта работа требует времени О ((V + Е) a (V)), где a — очень медленно растущая функция. Поскольку мы предполагаем, что G — связный граф, справедливо соотношение |E| ³ |V| - 1, так что операции над
непересекающимися множествами требуют О (Еa(V)) времени. Кроме того, поскольку a(|V|) = О (lgV) = O(lgE), общее время работы алгоритма Крускала равно О (ElgE). Заметим, что |Е| < |V|2, поэтому lg |E| = О (lg V) и время работы алгоритма Крускала можно записать как О (Е lg V).
Алгоритм Прима
Алгоритм Прима обладает тем свойством, что ребра в множестве А всегда образуют единое дерево. Дерево начинается с произвольной корневой вершины r и растет до тех пор, пока не охватит все вершины в V. На каждом шаге к дереву А добавляется легкое ребро, соединяющее дерево и отдельную вершину из оставшейся части графа. В соответствии со сказанным выше (утв.2) данное правило добавляет только безопасные для А ребра; следовательно, по завершении алгоритма ребра в А образуют минимальное остовное дерево. Данная стратегия является жадной, поскольку на каждом шаге к дереву добавляется ребро, которое вносит минимально возможный вклад в общий вес.
Ключевым моментом в эффективной реализации алгоритма Прима является выбор нового ребра для добавления в дерево. В приведенном ниже псевдокоде в качестве входных данных алгоритму передаются связный граф G и корень r минимального остовного дерева. В процессе работы алгоритма все вершины, которые не входят в дерево, располагаются в очереди с приоритетами Q, основанной на значении поля key, причем меньшее значение этого поля означает более высокий приоритет в очереди. Для каждой вершины v значение поля key [v] представляет собой минимальный вес среди всех ребер, соединяющих v с вершиной в дереве. Если ни одного такого ребра нет, считаем, что key [v] = ¥. Поле p[v] указывает родителя v в дереве. В процессе работы алгоритма множество А из процедуры Generic_MST неявно поддерживается как
А = {(v,p[v]) : v ÎV - {r} – Q} .
Когда алгоритм завершает работу, очередь с приоритетами Q пуста и минимальным остовным деревом для G является дерево
