
telnov-mechanika-and-TO
.pdf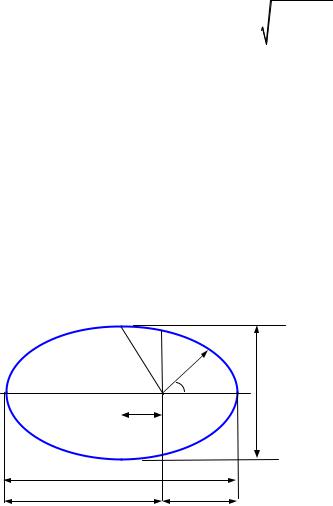
|
p |
= 1 +e cos j , |
(70.4) |
|||
|
r |
|
|
|
|
|
где введены обозначения |
|
|
|
|
|
|
p = |
L2 |
, e = |
1 + |
2EL2 . |
(70.5) |
|
ma |
||||||
|
|
|
ma2 |
|
||
Это кривые, соответствующие коническим сечениям (кривые, по которым поверхность круглого конуса пересекается плоскостью, см. курс аналитической геометрии). Величины p и e называются
параметром и эксцентриситетом орбиты.
В аналитической геометрии показывается, что при e = 0 – это круг;
e <1 – эллипс (E < 0 -финитная траектория); e = 1– парабола (E = 0 );
e > 1 – гипербола (E > 0 ).
Рассмотрим случай эллиптической траектории. Как известно, у эллипса имеется два фокуса, и сумма расстояний от фокусов до любой
|
|
|
|
|
|
|
|
|
|
|
|
|
|
точки постоянна. Уравне- |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ние эллипса в декартовых |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
b |
|
a |
p |
|
|
|
|
|
|
|
|
|
координатах |
|
|||
|
|
|
|
j |
|
|
|
|
|
|
|
x2 |
y2 |
|
||||
|
|
|
|
|
|
|
|
2b |
|
|
|
(70.6) |
||||||
O¢ |
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 |
+ b2 = 1 |
|||
C c |
O |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Центр тяготения находится |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в одном из фокусов, пусть |
||||
|
|
2a |
|
|
|
|
|
|
|
|
|
|
в правом, рис. 51. Из (70.4) |
|||||
rmax |
|
|
|
|
rmin |
|
|
|
|
|
минимальное |
расстояние |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
от фокуса (перигелий) и |
||||
|
Рис. 51 |
|
|
|
|
|
|
|
|
|
|
максимальное |
расстояние |
|||||
|
|
|
|
|
|
|
|
|
|
|
(афелий) |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
r |
|
= |
|
|
p |
, |
r |
|
= |
|
|
p |
; |
|
(70.7) |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
min |
|
1 |
+e |
|
max |
|
1 |
+e |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
параметр p равен радиусу при j |
= p |
, большая полуось |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
171
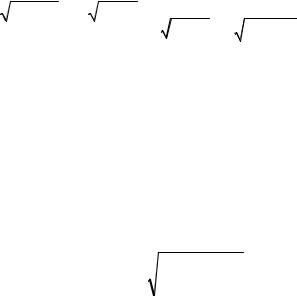
a = |
1 |
(r |
+r ) = |
p |
= - |
a |
= |
a |
, |
(70.8) |
|
2 |
1 -e2 |
2E |
2 | E | |
||||||||
|
min |
max |
|
|
|
|
(при финитном движении энергия отрицательна, поэтому здесь использован модуль E , чтобы знак минус не вводил в заблуждение),
отсюда |
|
|
|
|
|
|
|
rmin = a(1 -e), |
rmax |
= a(1 +e). |
(70.9) |
||||
Расстояние между фокусом и центром эллипса |
|
|
|
||||
c = 0.5(rmax -rmin ) = ae; |
|
|
(70.10) |
||||
малая полуось |
|
|
|
|
|
|
|
b = a2 -c2 = a 1 -e2 |
= |
|
p |
= |
L |
. |
(70.11) |
|
|
|
|||||
|
|
|
1 -e2 |
2m | E | |
|
||
Как мы видим, большая полуось a зависит только от полной энергии, а малая полуось зависит также от момента импульса.
Заметим, что выражение для rmax,rmin и a легко получить из законов
сохранения энергии и момента импульса. Действительно, для перигелия и афелия нет радиального движения и
L = mvr, |
E = mv2 |
- a |
, |
|
(70.12) |
||||||||
|
|
|
|
|
2 |
|
|
|
r |
|
|
|
|
отсюда |
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
= - |
a |
|
a2 |
|
+ |
L2 |
, |
(70.13) |
||||
2E |
4E2 |
2mE |
|||||||||||
max,min |
|
|
|
|
|
|
|
||||||
a = |
1 |
(r +r |
) = - |
a |
, |
|
(70.14) |
||||||
2 |
2E |
|
|||||||||||
|
min |
max |
|
|
|
|
|
|
|||||
что совпадает с (70.8) и (70.9).
172

Период обращения
Из сохранения момента импульса
2 |
dS |
|
|
L |
|
|
L = mr j |
= 2m dt |
, |
S = |
|
T, |
(70.15) |
2m |
||||||
где T – период обращения. Учитывая, что для эллипса S = pab получаем
T = |
2pmab |
= pa |
|
m |
|
= 2pa3/2 |
m . |
(70.16) |
L |
|
2 | E |3 |
||||||
|
|
|
|
a |
|
|||
Отсюда следует третий закон Кеплера |
|
|
|
|||||
|
|
T 2 = |
4p2m a3 . |
|
|
(70.17) |
||
|
|
|
|
a |
|
|
|
|
Этот закон легко получить в случае кругового движения, но оказывается формула остается справедливой и для эллиптического движения, если вместо радиуса в формуле использовать большую полуось эллипса. Для гравитационного взаимодействия тел с массами M и m
a =GMm, |
m m = |
Mm |
, |
(70.18) |
|
M +m |
|||||
|
|
|
|
Случай e = 1,
Dj
Рис. 52
T 2 = |
|
|
4p2a3 |
. |
|
(70.19) |
||
G(M +m) |
||||||||
|
|
|
|
|||||
E = 0 -парабола |
|
|
|
|
|
|||
Из (70.4) следует, что в этом случае |
|
|||||||
r |
= p = |
L2 |
|
(70.20) |
||||
|
||||||||
|
min |
|
|
|
|
|
||
j |
2 2ma |
|
и угол поворота при облете центра тяготения Dj = 2p, т.е. траектория поворачивает в об-
ратную сторону ( cos 1 при r ). Вы-
ражение (70.20) также легко получить из законов сохранения энергии и момента импульса, полагая в них E = 0
173

L = mvr, |
E = mv2 |
- a |
= 0. |
(70.21) |
|
2 |
r |
|
|
Случай e > 1, E > 0 - гипербола
Гипербола – геометрическое место точек, для которых абсолютная величина разности расстояний до двух заданных точек (фокусов) (-c, 0),
(c, 0)постоянна и равна 2a < 2c . Уравнение гиперболы в декартовых координатах
|
x2 |
- y2 |
= 1 . |
|
|
|
|
|
|
|
(70.22) |
|||||||
|
a2 |
|
|
b2 |
|
|
|
|
|
|
|
|
|
|
|
|||
В полярных координатах (70.4) |
|
p |
= 1 +e cos j, |
e > 1 . |
|
|||||||||||||
Минимальное расстояние равно |
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
r |
|
|
= |
|
|
p |
. |
|
|
|
|
|
|
|
(70.23) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
min |
|
|
e +1 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Полагая r = ¥, находим cos j = - |
1 . Половина угла поворота траек- |
|||||||||||||||||
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
тории при пролете мимо центра тяготения, см. рис. 52, |
|
|||||||||||||||||
|
|
p |
|
|
|
|
|
|
|
æ |
|
|
ö |
|
p |
|
|
|
Dj = j - |
|
|
|
|
|
|
|
ç |
|
1÷ |
- |
|
(70.24) |
|||||
|
|
= arccosç- |
|
÷ |
|
|
||||||||||||
|
|
2 |
|
|
|
|
|
|
|
ç |
|
e |
÷ |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
ø |
|
|
|
||||
отсюда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
æ |
ö |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
ç |
p÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
(70.25) |
|||
-cosçDj + |
÷ = sin Dj = |
|
= |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|||||||||||||
ç |
÷ |
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
2 |
|
è |
2 ø |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
+ |
2EL |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ma2 |
|
Если частица имела на бесконечности скорость v¥ и прицельный
параметр (расстояние между продолжением исходной траектории и центром тяготения) r, то подставляя в (70.25)
L = mrv |
|
, E = |
|
mv |
2 |
, |
(70.26) |
|
|
|
|
¥ |
|||||
¥ |
2 |
|
||||||
|
|
|
|
|
|
|||
нетрудно получить |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
tg Dj = |
a |
= GM |
. |
|
(70.27) |
|||
2rE |
|
|||||||
|
|
|
rv2 |
|
|
|
||
|
|
|
|
¥ |
|
|
|
|
174

|
Проследим эволюцию орбит при измерении |
|
параметров. Пусть тела пролетают на од- |
|
ном и том же расстоянии от центра тяготе- |
|
ния, но с разными скоростями, рис. 53. При |
|
малой скорости центр тяготения находится |
|
в правом фокусе эллиптической орбиты. |
|
При увеличении скорости орбита становит- |
|
ся круговой. При еще большей скорости |
|
орбита становится снова эллиптической, но |
|
центр тяготения находится уже в левом фо- |
|
кусе эллипса. При еще большей скорости |
Рис. 53 |
траектория становится гиперболической. |
|
Случай отталкивающего потенциала
Пусть
U = a |
, |
U |
|
= a |
+ |
L2 |
, |
a>0 . |
(70.28) |
|
эф |
2mr2 |
|||||||||
r |
|
|
r |
|
|
|
|
После вычислений аналогичных (70.2) получается уравнение траектории отличающееся от (70.4) только знаком минус перед единицей
где p
O
|
p |
= -1 +e cos j, |
|
|
|
(70.29) |
|||
|
r |
|
|
|
|
|
|
|
|
и e |
даются прежними формулами (70.5). Расстояние в периге- |
||||||||
|
|
лии |
|
|
|
|
|
|
|
|
|
|
r |
|
= |
|
p |
. |
(70.30) |
|
|
|
|
|
|
||||
|
|
|
min |
|
e -1 |
|
|||
|
|
|
|
|
|
|
|||
Dj |
r |
Половина |
полного угла |
поворота при |
|||||
|
j |
пролете |
мимо |
отталкивающего центра |
|||||
|
Dj = p |
-j. При r = ¥ из (70.29) име- |
|||||||
|
|
||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
ем cos j = |
1 , тогда |
|
|||||
|
|
|
|
e |
|
|
|
|
|
Рис. 54
175

æ |
|
ö |
|
1 |
|
|
çp |
÷ |
= cos j = |
. |
(70.31) |
||
sin Dj = sinç |
|
-j÷ |
|
|||
ç |
2 |
÷ |
|
e |
|
|
è |
ø |
|
|
|
||
Из сравнения (70.31) и (70.25) следует, что угол отклонения для притягивающего и отталкивающего потенциалов одинаковы! Это весьма неочевидный результат. Половинный угол поворота для частицы, летящей с бесконечности, будет даваться той же формулой (70.27). Разница только в том, что в случае притяжения частица отклоняется в сторону центра притяжения, а в случае отталкивания в обратную сторону.
Конические сечения.
Выше было декларировано, что формула (70.4) описывает эллипсы, параболы, гиперболы. Покажем это. Учитывая, что cos x / r , запи-
шем (70.4) в виде |
|
r = p -xe . |
(70.32) |
Возводя в квадрат, получаем |
|
x2 y2 p2 2 pxe x2e2 .
Далее, после перегруппировки членов получается
1) |
e 1 (эллипс) |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
pe |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
y |
2 |
|
|
|
|
|
p |
|
|
|||||
|
1 e |
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
, где a |
|
|
и b |
||||||||||||
|
|
|
|
|
|
a2 |
|
|
|
|
|
|
|
b2 |
1 e2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
2) |
e 1 (парабола) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y2 2 p x |
. |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|||||||||
3) |
e 1 (гипербола) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
pe |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
y |
2 |
|
|
|
|
|
|
|
p |
|
|
|||||
|
e |
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
, |
где a |
|
|
и b |
||||||||||||||
|
|
|
|
|
a2 |
|
|
|
|
|
|
b2 |
|
|
|
e2 1 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
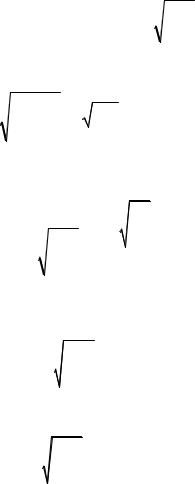
(70.33)
p |
|
1 e2 . |
(70.34) |
|
(70.35) |
p |
.(70.36) |
e2 1 |
176
§ 71. Полеты в космос
Движение по круговой орбите.
При движении по круговой орбите вокруг Земли
mv2 |
= GMm |
v = |
GM . |
(71.1) |
2 |
r |
|
r |
|
Если спутник находится на низкой орбите около Земли, то r = RЗ и
v = |
GM R = |
gR = 7.9 км/с, |
(71.2) |
1 |
R2 З |
З |
|
|
З |
|
|
– это первая космическая скорость. Период обращения спутника на околоземной орбите
T = |
2pRЗ |
= 2p |
RЗ |
= 88 мин. . |
(65) |
||||
|
|
|
|||||||
|
|
GM |
|
|
g |
|
|||
|
|
|
RЗ |
|
|
|
|
|
|
Для спутников на геостационарной орбите |
|
||||||||
T = |
2prГ |
|
= 1 сутки. |
(71.3) |
|||||
|
|
||||||||
|
|
|
GM |
|
|||||
|
|
|
rГ |
|
|
|
|
|
|
Отсюда rГ = 42.2 км и скорость и |
|
|
|
|
|
||||
v |
= GM |
= 3.07 км/с. |
(71.4) |
||||||
Г |
|
|
rГ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Вторая космическая скорость.
Для вылета на пределы Земли необходимо чтобы движение было инфинитно, а для этого, как было установлено ранее (в предыдущей лекции), необходимо
177
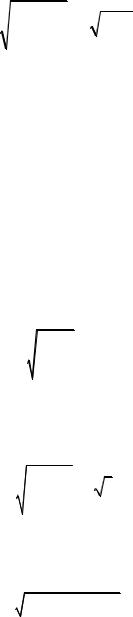
E = mv2 |
-GMm |
> 0 . |
(71.5) |
2 |
R |
|
|
|
З |
|
|
Заметим, что эта скорость не зависит от направления запуска ракеты. Минимальная скорость
v |
= |
2GM R = |
2gR = 11.2 км/с, |
(71.6) |
2 |
|
R2 З |
З |
|
|
|
З |
|
|
– это вторая космическая скорость.
Если скорость ракеты на поверхности Земли v , то скорость на бесконечности (r RЗ ) находится из закона сохранения энергии
|
|
mv¥2 |
= mv2 |
-GMm |
= mv2 |
- |
mv22 |
|
(71.7) |
|
2 |
|
|||||||
|
2 |
R |
2 |
2 |
|
|
|||
|
|
|
|
З |
|
|
|
|
|
отсюда |
v¥2 = v2 -(11.2)2, где скорости в км/с. |
(71.8) |
|||||||
Третья космическая скорость.
Найдем скорость, необходимую для полета за пределы Солнечной системы. Скорость Земли на орбите вокруг Солнца (аналог первой космической скорости)
v |
= |
GMC |
= 29.76 » 30 км/с. |
(71.9) |
|
||||
1C |
|
rЗ |
|
|
|
|
|
||
Здесь rЗ – радиус орбиты Земли вокруг Солнца, MC – масса Солнца.
Для полета на бесконечность с орбиты Земли в поле Солнца необходима вторая солнечная космическая скорость
v |
|
= |
2GMC |
= 2v |
= 42.1 км/с. |
(71.10) |
2C |
|
|||||
|
|
|
1С |
|
|
|
|
|
|
rЗ |
|
|
|
Т.е. вдобавок к орбитальной скорости Земли нужно иметь дополнительную скорость 42 30 12 км/с. Это значит, что на поверхности Земли ракета должна иметь скорость, см. (71.8)
v = (12)2 +(11.2)2 = 16.4 км/с. |
(71.11) |
178

Полет на Марс
Самым экономичным полетом к Марсу является полет, когда ракета стартует вдоль орбитальной скорости Земли и далее, двигаясь по эллипсу, касается орбиты Марса, рис.55. Дей-
ствительно, согласно (70.8) полная энергия E 2GMma . Отсюда начальная кинетическая
энергия при старте с орбиты Земли
Рис. 55
K |
|
= - |
2GMm |
-U |
|
= - |
2GMm |
+ |
GMm |
, |
(71.12) |
0 |
|
0 |
|
|
|||||||
|
|
a |
|
|
a |
|
rЗ |
|
|||
|
|
|
|
|
|
|
|
||||
и она уменьшается при уменьшении большой полуоси эллипса. Продолжительность полета (туда-обратно) находится из (70.19)
T 2 = |
4p2a3 |
= |
4p2(rЗ +rМ )3 |
. |
(71.13) |
|
|
||||
|
GMС |
|
8GMС |
|
|
Его можно выразить через периоды обращения Земли и Марса
T 2 |
= |
4p2rЗ3 |
, T 2 |
= |
4p2rM3 |
. |
(71.14), |
|
|
||||||
З |
|
GMС |
M |
|
GMC |
|
|
|
|
|
|
|
|||
В результате с учетом TЗ = 1 год, TM = 1.88 года , получаем
|
|
|
8 |
( З |
M |
) |
|
|
|
||
T |
2 |
= |
1 |
T |
2/3 |
+T |
2/3 |
3 |
T = 1.42 |
года. |
(71.15) |
|
|
|
|
|
|||||||
Полная энергия ракеты при движении по эллипсу дается ф-лой (70.8)
E = -GMC m . rЗ +rM
Скорость ракеты на орбите Земли vЗ находится из
|
mv2 |
|
GMC m |
|
GMC m |
. |
|||
E = |
З |
- |
|
|
= - |
|
|
|
|
2 |
|
r |
|
r |
+r |
||||
|
|
|
|
|
|
||||
|
|
|
|
З |
|
|
З |
M |
|
(71.16)
(71.17)
179
откуда |
|
|
|
|
|
|
|
|
|||
v |
З |
= |
2GMC rM |
|
= v |
|
rM |
|
» 42.1 0.78 = 32.7 км/с. (71.18) |
||
r (r +r ) |
2C |
r +r |
|||||||||
|
|
|
|
||||||||
|
|
|
З M |
З |
|
|
З |
M |
|
||
Поскольку имеется скорость орбитального движения Земли 29.76 км/с, то необходимая добавочная скорость 32.7 -29.76 » 2.95 км/с. Для этого стартовая скорость ракеты на поверхности Земли должна быть
(см. (71.8))
v = (2.95)2 +(11.2)2 = 11.6 км / с. |
(71.19) |
Это и есть искомая скорость ракеты для полета на Марс. Она лишь немного больше второй космической скорости.
Заметим, что формулу (71.18) можно легко получить не прибегая к общему решению движения по эллиптическим орбитам. В точках, где орбита ракеты касается орбит Земли и Марса скорость ракеты перпендикулярна радиусу. Законы сохранения момента импульса и энергии для этих двух точек
|
|
|
vЗrЗ = vMrM, |
|
|
|
(71.20) |
||||
v2 |
|
GM |
C |
|
v2 |
|
GM |
C |
, |
(71.21) |
|
З |
- |
|
|
= |
M |
- |
|
||||
2 |
|
r |
|
2 |
r |
|
|||||
|
|
|
|
|
|
|
|
||||
|
|
|
З |
|
|
|
|
M |
|
|
|
откуда, сразу получаем для vЗ выражение, совпадающее с (71.18).
Долететь до Марса не так сложно, труднее вернуться. Вторая космическая скорость для Марса около 5 км/с (для Луны 2.375 км/с), так, что стартовая масса посадочного модуля должна быть достаточно большая. Возможно, первые покорители Марса полетят в одну сторону. Сначала с помощью роботов построят жилище, завод по производству товаров жизненной необходимости, а затем полетят люди— «переселенцы». Еще одна проблема—это очень высокая радиация во время полета и на поверхности Марса. Доза, получаемая во время полета, составляет порядка 100 бэр (1 Зиверт), что является предельно допустимой для людей. На поверхности Марса радиация примерно втрое выше, чем на орбитальной станции, но там хоть можно спрятаться.
180
