10_11_konspekt

Лекция 7. Пятый постулат Евклида и его равносильность аксиоме параллельности. Эквивалентность пятого постулата Евклида и утверждения Фаракаша Бояи аксиоме параллельности евклидовой геометрии. Теоремы Лежандра. Сумма углов треугольника и его связь с аксиомой параллельности. Предложения Валлиса Лежандра и аксиома параллельности. Предложение Посейдония.

Литература [2] § 16 – 19.

Утверждения абсолютной геометрии.

Если вспомнить историческую справку, то можно сделать вывод, изучению свойств пространства Лобачевского предшествовали исследования роли и места аксиомы параллельности и утверждений ей эквивалентных в элементарной геометрии. Эти исследования, по сути, лежат в основе начал геометрии Лобачевского. На наш взгляд они крайне важны учителю математики, так как раскрывают роль и устанавливают значение аксиомы параллельности в утверждениях школьного курса геометрии. Напомним, что два утверждения называются эквивалентными, если при условии, что первое из них истинно, из него вытекает второе, и, наоборот, из истинности второго следует справедливость первого. Мы будем предполагать, что все наши исследования проводятся в трехмерном евклидовом пространстве, построенном на основании аксиоматики Гильберта. Напомним также, что утверждения, доказанные на основе первых четырех групп аксиом Гильберта, т.е. при доказательстве которых не используется аксиома параллельности, относятся к так называемой абсолютной геометрии. Ранее мы сформулировали, а также доказали ряд утверждений абсолютной геометрии, которые нам понадобятся в дальнейшем. Приведем их формулировки, сохранив при этом ту нумерацию доказанных утверждений, которую мы использовали в упомянутом параграфе.

В равнобедренном треугольнике углы при основании равны между собой.

Справедливы первый, второй и третий признаки равенства треугольников.

Вертикальные углы равны между собой.

Любые два прямых угла конгруэнтны между собой.

Через любую точку прямой можно провести перпендикулярную к ней прямую.

Теорема 4.1. (Теорема о внешнем угле треугольника). Внешний угол треугольника больше любого внутреннего, не смежного с ним.

Теорема 4.2. Если при пересечении двух прямых a и b третьей соответственные углы  и  равны между собой, то прямые  и  не пересекаются.

Если при пересечении двух прямых a и b третьей прямой с накрест лежащие углы равны между собой, или сумма внутренних односторонних равна развернутому углу, то прямые a и b не пересекаются.

V₁. (Аксиома параллельности евклидовой геометрии). Пусть а – произвольная прямая, А – точка, не лежащая на этой прямой. Тогда в плоскости, определяемой точкой А и прямой а, существует не более одной прямой, проходящей через А и не пересекающей прямую а.

Если две прямые при пересечении с третьей образуют с одной стороны внутренние односторонние углы, сумма которых меньше двух прямых, то эти прямые пересекались бы при достаточном продолжении с этой стороны.

Теорема 9.1. Пятый постулат Евклида эквивалентен аксиоме параллельности евклидовой плоскости.

Д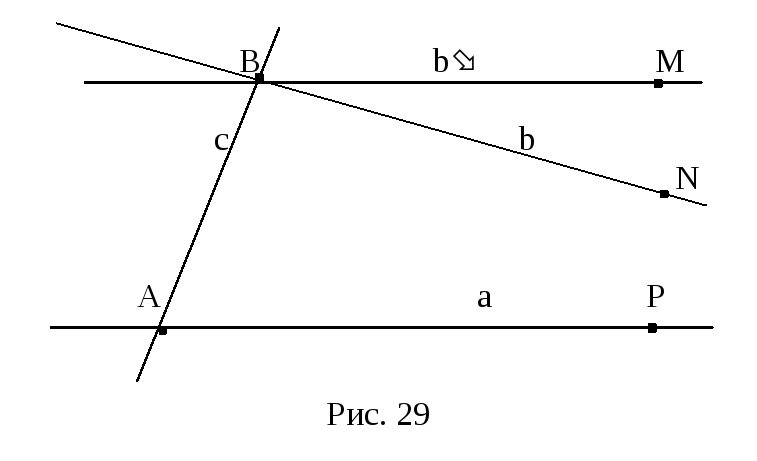оказательство. Докажем, что при условии выполнения аксиомы параллельности евклидовой геометрии справедлив пятый постулат Евклида. Предположи противное. Пусть даны две прямые a и b, которые не пересекаются и при пересечении третьей прямой c образуют с ней внутренние односторонние углы сумма которых меньше двух прямых (рис. 29):

. (1) ¹

Проведем через точку В прямую b, так, чтобы

(2)

(см. рис 29). Тогда в силу теоремы 4.2 прямые a и b не пересекаются. Из соотношений (1) и (2) следует, что прямые b и b различны. Мы пришли к противоречию с аксиомой параллельности евклидовой плоскости. Через точку В проходят две различные прямые b и b, которые не пересекают прямую а.

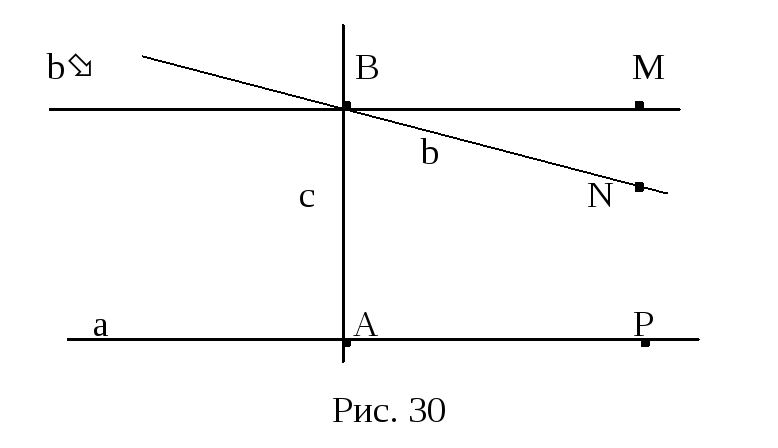
Обратно, пусть выполнено требование пятого постулата Евклида. Рассмотрим произвольную точку В и прямую а, ее не содержащую. Опустим из точки В перпендикуляр с на прямую а и восставим в этой же точке перпендикуляр b к прямой с (рис 30). Из теоремы 4.2 следует, что прямые a и b не пересекаются. Проведем через точку В произвольную прямую, отличную от b. Так как b и b не совпадают друг с другом, то один из углов, который прямая b образует с прямой c, отличен от прямого угла. На рисунке 30 таким углом является . Таким образом . В силу условия пятого постулата Евклида, прямые а и b имеют общую точку. Любая прямая, проходящая через точку В и отличная от прямой b, пересекает прямую а. Теорема доказана

В конце 18 и начале 19 веков известный венгерский математик Фаркаш Бояи, отец одного из первооткрывателей геометрии Лобачевского Яноша Бояи (см. § 8), предпринимал безуспешные попытки доказательства пятого постулата Евклида. Он привел доказательство пятого постулата, но при следующем неявном допущении: вокруг любого треугольника на плоскости можно описать окружность. Покажем, что это утверждение равносильно аксиоме параллельности евклидовой геометрии.

Прежде всего, напомним известный факт из школьного курса геометрии: если вокруг треугольника можно описать окружности, то ее центр лежит в точке пересечения серединных перпендикуляров. И, наоборот, если два серединных перпендикуляра треугольника пересекаются, то их общая точка служит центром описанной окружности этого треугольника и через нее проходит серединный перпендикуляр к третьей стороне.

Теорема 2. Утверждение: вокруг любого треугольника на плоскости можно описать окружность, равносильно аксиоме параллельности евклидовой геометрии.

Д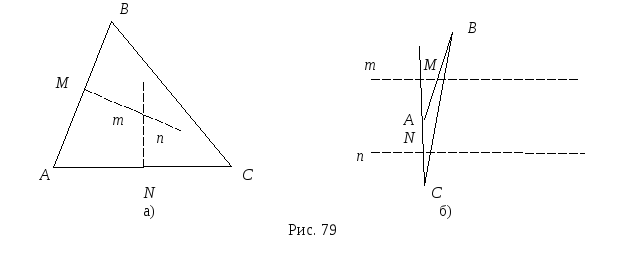оказательство. Предположим, что на плоскости выполнена аксиома Плейфера, через точку, не лежащую на данной прямой, проходит не более одной прямой, не пересекающей данную. Тогда если прямые не пересекаются, то при пересечении третьей прямой накрест лежащие углы равны между собой. Рассмотрим треугольник АВС. Пусть М и N середины сторон АВ и АС, а m и n соответственно серединные перпендикуляры, восставленные в этих точках (рис. 79, а). Предположим, что серединные перпендикуляры m и n не пересекаются (рис 79, б). Тогда углы между прямыми АС и n и прямыми АВ и m – прямые. Прямая АС пересекает прямую m. Действительно, если предположить противное, то АС параллельна m. Тогда через точку N проходит две прямые, параллельные m, что противоречит аксиоме Плейфера. Поэтому, в силу признака параллельности прямых на евклидовой плоскости угол между m и АС прямой. С другой стороны, прямая m серединный перпендикуляр к прямой АВ. Таким образом, из точки А мы провели два перпендикуляра к прямой m, чего не может быть. Построенное противоречие опровергает наше предположение, серединные перпендикуляры m и n пересекаются. Вокруг любого треугольника на евклидовой плоскости можно описать окружность.

Обратно. Предположим, что вокруг любого треугольника на плоскости можно описать окружность. Пусть дана произвольная прямая а и точка В, которая ей не принадлежит. Опустим из точки В перпендикуляр с на прямую а. Н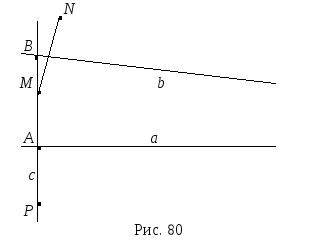ам достаточно доказать, что любая прямая b, проходящая через точку В и неперпендикулярная прямой с, пересекается с прямой а. Ясно, что тогда будет выполняться аксиома Плейфера. Рассмотрим такую прямую b (рис. 80). Выберем на отрезке АВ произвольную точку М. Отразим ее симметрично относительно прямых a и b. Получим соответственно точки P и N. Так как прямые а и с перпендикулярны, то точка Р принадлежит прямой с. С другой стороны, прямые с и b не перпендикулярны друг другу, поэтому точка N не лежит на прямой с. Точки P, M и N являются вершинами треугольника, а прямые a и b служат его серединными перпендикулярами. Они, в силу предположения, пересекаются в центре окружности, описанной вокруг треугольника PMN. Теорема доказана.

Теоремы Лежандра являются утверждениями абсолютной геометрии, поэтому при доказательстве всех утверждений настоящего параграфа мы не будет использовать аксиому V₁ параллельности евклидовой геометрии. В основе наших утверждений будем лежать аксиомы I₁ – VI₂ аксиоматики Гильберта евклидовой геометрии.

При изучении свойств треугольника естественно возникает вопрос о сумме его углов. Из школьного курса геометрии известно, что на евклидовой плоскости сумма углов треугольника равна двум прямым углам. Какие ограничения наложены на это число в абсолютной геометрии? Ответ на этот вопрос дает следующая теорема.

Теорема 10.1 (Первая теорема Лежандра). Сумма углов треугольника не может превышать двух прямых углов.

Д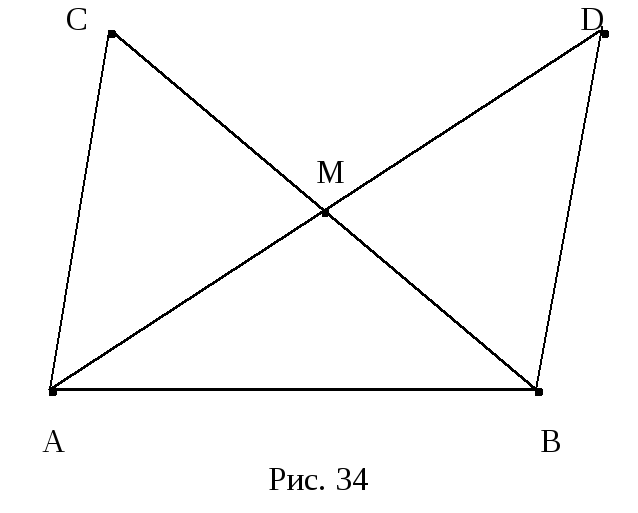оказательство. Введем следующее обозначение. Сумму углов произвольного треугольника АВС будем обозначать через (АВС). Пусть дан произвольный треугольник АВС, тогда существует такой треугольник, у которого, во первых, угол А₁ меньше или равен половине угла А треугольника АВС: , и, во вторых, . Рассмотрим середину М стороны АВ исходного треугольника (рис. 34). Отложим на луче АМ от точки М отрезок MD, равный АМ. Получим треугольник ABD. Отрезок СМ равен отрезку МВ, так как М середина отрезка СВ, по построению, как вертикальные, поэтому треугольники АМС и BMD равны между собой по первому признаку равенству треугольников. Отсюда следует, что . Следовательно,

. (1)

Мы получили, что в треугольнике ABD один из углов или меньше или равен половине треугольника АВС. Из равенства треугольников АМС и BMD также следует, что . Отсюда и из (1) вытекает, что

.

Треугольник ABD искомый. Осталось только переименовать его вершины, обозначив при этом через А₁ ту из них, угол при которой меньше или равен половине треугольника АВС.

Ясно, что, повторяя этот процесс n раз мы придем к треугольнику , сумма углов которого равна сумме углов треугольника АВС, угол при вершине которого удовлетворяет неравенству:

. (2)

Предположим, что существует треугольник АВС, такой, что

. (3)

Используя предыдущие рассуждения, построим треугольник , для которого сумма углов равна сумме углов треугольника АВС:

, (4)

угол которого удовлетворяет неравенству (2). При этом выберем число n так, чтобы

.

Тогда из соотношений (2) – (4) следует,

. (5)

И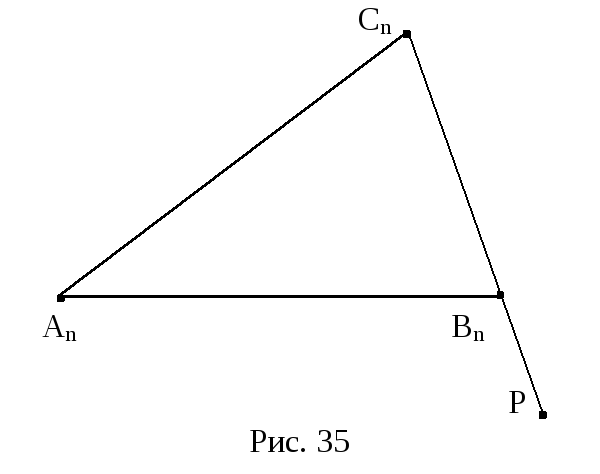спользуя теорему 4.1 о внешнем угле треугольника, нетрудно, доказать, что не существует треугольника, сумма двух углов которого больше двух прямых углов. Действительно, пусть - внешний угол при вершине B_n треугольника (рис. 35). Тогда их теоремы о внешнем угле треугольника следует:

. (6)

Но . Из неравенства (5) вытекает: . Мы пришли к противоречию с неравенством (6). Теорема доказана.

Определение 10.1. Дефектом треугольника АВС называется разность между развернутым углом и суммой его углов:

Из первой теоремы Лежандра следует, что

. (7)

Рассмотрим свойства этого понятия.

С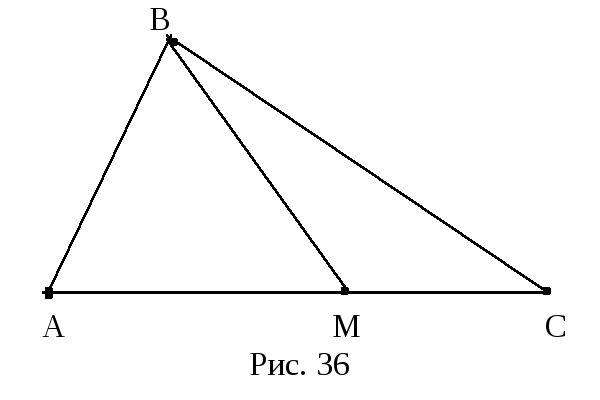войство 10.2. Пусть дан треугольник АВС, точка М принадлежит его стороне АС. Тогда:

. (8)

Доказательство. Так как точка М принадлежит стороне АС данного треугольника, то (рис. 36). Кроме того, сумма углов при вершине М треугольников АВМ и ВМС равна развернутому углу . Из полученных равенств следует:

Свойство доказано.

Свойство 10.3. Если точка М принадлежит стороне АС треугольника АВС, то

(9)

Доказательство этого свойства непосредственно следует из неравенства (7) и равенства (8).

С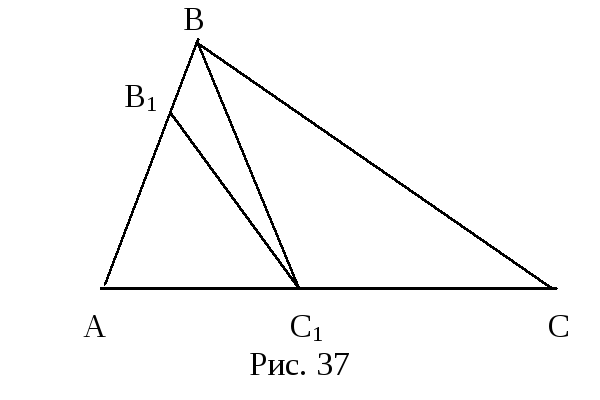войство 10.4. Если точка М принадлежит стороне АС треугольника АВС и , то дефект треугольника АВМ также равен нулю.

Доказательство этого свойства вытекает из неравенств (7) и (9).

Свойство 10.5. Если точки В₁ и С₁ принадлежат соответственно сторонам АВ и АС треугольника АВС, то

. (10)

Для доказательства достаточно провести отрезок ВС₁. Из свойства 10.3 следует, что и . Откуда и следует искомое неравенство.

Свойство 10.6. Если точки В₁ и С₁ принадлежат соответственно сторонам АВ и АС треугольника АВС, и , то .

Доказательство этого свойств вытекает из неравенств (7) и (10).

Рассмотрев свойства дефекта треугольника, мы можем приступить к доказательству второй теоремы Лежандра. Напомним, что доказательство проводится в условиях абсолютной геометрии.

Теорема 10.7. (Вторая теорема Лежандра). Если на плоскости существует хотя бы один треугольник, сумма углов которого равна двум прямым углам, то сумма углов любого другого треугольника также равна развернутому углу.

Доказательство. Нам достаточно доказать, что из равенства нулю дефекта какого либо треугольника на плоскости следует равенство нулю дефекта любого другого треугольника. Прежде всего, докажем это утверждение для прямоугольных треугольников.

Лемма 10.8. Если дефект какого либо прямоугольного треугольника на плоскости равен нулю, то дефект любого другого прямоугольного треугольника также равен нулю.

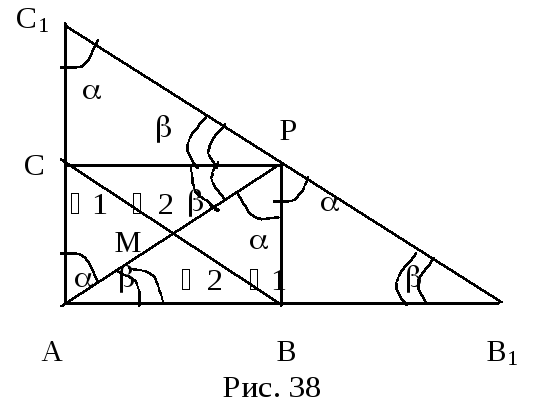
Доказательство. Пусть АВС – прямоугольный треугольник с прямым углом А, дефект которого равен нулю, М – середина гипотенузы СВ. Построим точки В₁, С₁ и Р, симметричные точке А относительно точек В, С и М (рис.38). Обозначим угол САМ через , а угол ВАМ – через . По условию треугольник АВС – прямоугольный, следовательно

. (11)

Ведем также обозначения:

.

Так как по условию дефект треугольника АВС равен нулю, то

(12)

Так как точки А и Р симметричны относительно середины гипотенузы М, то

(докажите эти равенства самостоятельно). Отсюда следует, что , и . В силу равенства (12) . Аналогично, . Прямая ВР перпендикулярна АВ, а прямая РС перпендикулярна АС. Треугольники АВР и АСР – прямоугольные. По построению точки А и В₁ центрально симметричны относительно точки В, следовательно они симметричны относительно прямой РВ. Отсюда следует, что

, (13)

и треугольники ВРВ₁ и СРС₁ также прямоугольные. Из равенств треугольников (13) вытекает, что , и . Таким образом, в силу равенства (11), . Угол С₁РВ₁ – развернутый, точки С₁, Р и В₁ лежат на одной прямой. Из равенств (13) также следует, что и . Мы построили прямоугольный треугольник АВ₁С₁, стороны которого в два раза больше сторон исходного треугольника АВС, дефект которого равен 0 (см. (11)). Ясно, что, продолжая этот процесс, мы можем построить такой прямоугольный треугольник , для которого и .

Рассмотрим теперь произвольный прямоугольный треугольник RST с прямым углом R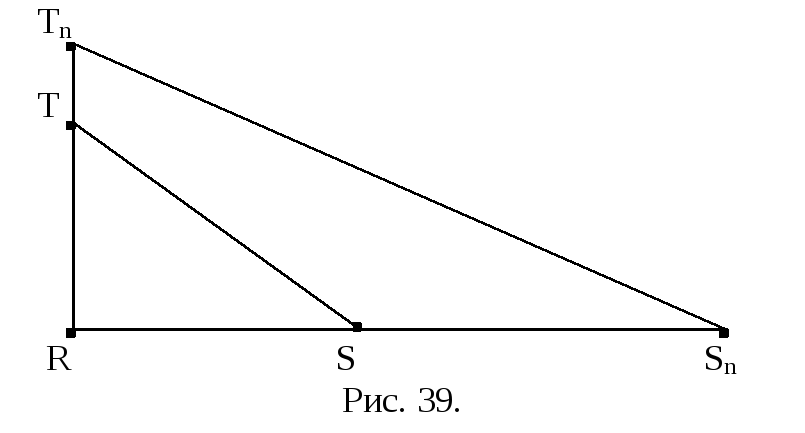. Выберем такое натуральное число n, чтобы катеты RS и RT удовлетворяли неравенствам:

,

где АВ и АС – катеты данного прямоугольного треугольника. Построим указанным выше способом прямоугольный треугольник , у которого , . Отложим на лучах RS и RT соответственно отрезки (рис. 39). Получим прямоугольный треугольник , равный . По построению треугольник имеет нулевой дефект и, в силу свойства 10.6, дефект треугольника RST равен нулю. Лемма доказана.

К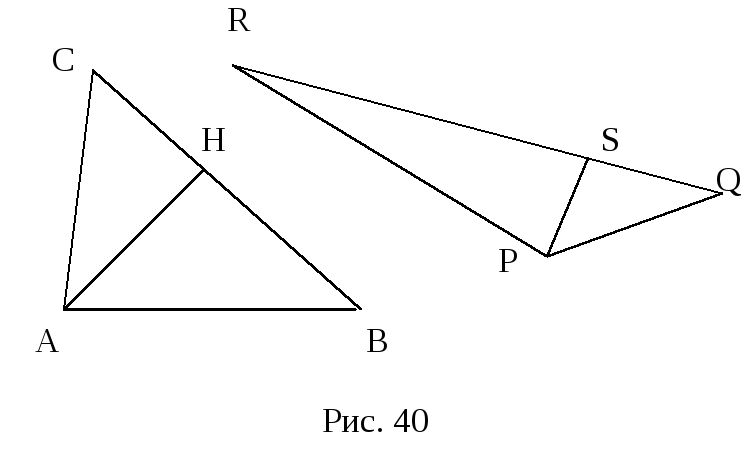ак мы видим, лемма 10.8 представляет собой частный случай второй теоремы Лежандра. С ее помощью легко доказать это утверждение в общем случае. Предварительно сделаем следующее замечание. Если дан не прямоугольный треугольник, то его всегда можно разбить на два прямоугольных треугольника. Для этого достаточно провести высоту к его большей стороне, которая будет лежать внутри треугольника. Доказательство этого факта проведите самостоятельно.

Пусть на плоскости дан произвольный треугольник АВС, дефект которого равен нулю. Рассмотрим второй произвольный треугольник PQR. Разобьем их соответственно на прямоугольные треугольники ACH, AHB и PSR, PSQ (рис. 40). Так как , то из свойства 10.5 следует, что дефекты прямоугольных треугольников AHB и AHC также раны нулю. Из леммы 10.8 вытекает, что дефект любого другого прямоугольного треугольника совпадает с нулем. Следовательно,

.

Так как треугольник PRQ «составлен» из прямоугольных треугольников RSP и PSQ, то из свойства 10.2 следует, . Теорема доказана.

Теоремы Лежандра имеют большое значение при построении основ неевклидовой геометрии Лобачевского. В следующем параграфе они будут использованы нами при доказательстве утверждений, равносильных аксиоме параллельности евклидовой геометрии.

Теорема 11.1. Предположение о существовании треугольника, сумма углов которого совпадает с суммой двух прямых углов, равносильно аксиоме параллельности евклидовой плоскости.

Доказательство. В евклидовой геометрии, как следует из школьного курса математики, сумма углов любого треугольника на плоскости равна развернутому углу. Нас интересует обратное утверждение. Пусть на плоскости дан треугольник, сумма углов которого равна двум прямым углам. Докажем, что тогда справедливо утверждение: если даны точка и прямая, принадлежащие плоскости, причем точка не лежит на прямой, то существует единственная прямая, проходящая через данную точку и не пересекающая данную прямую.

Из второй теоремы Лежандра следует, что в условиях нашей теоремы сумма углов любого треугольника на плоскости равна 2d. Легко видеть, что это утверждение равносильно следующему свойству внешнего угла треугольника.

Лемма 11.2. Сумма углов треугольника равна 2d тогда и только тогда, когда его внешний угол равен сумме внутренних углов, с ним не смежных.

Доказательство. Необходимость. Пусть в треугольнике АВС (рис. 41). Тогда . С другой стороны, внешний угол составляет с развернутый угол, поэтому . Отсюда следует, что .

Достаточность. Пусть . Так как , то . Отсюда следует, что . Лемма доказана.

Рассмотрим произвольную точку А и прямую m плоскости, точка А не принадлежит данной прямой. Опустим из точки А перпендикуляр АВ на прямую m (рис. 42) 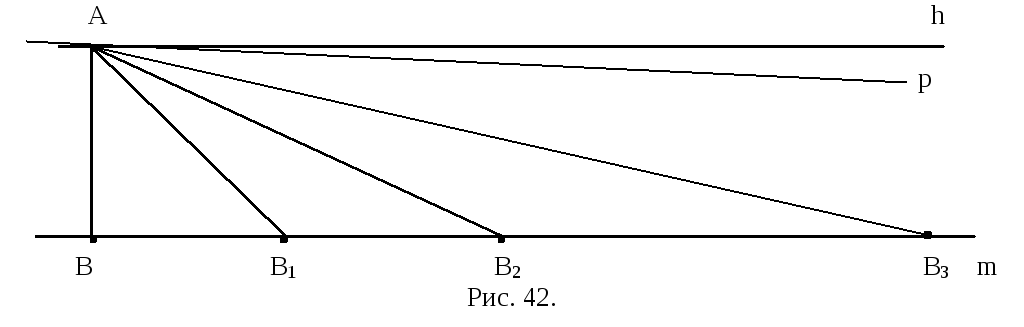и восставим в точке А перпендикуляр h к прямой АВ. Как известно, прямые m и h не пересекаются (теорема 4.2). Предположим, что через точку А проходит еще одна прямая р, отличная от h, не пересекающая m. Рассмотрим ту полуплоскость с границей АВ, в которой прямые p и h образуют острый угол. Отложим в этой полуплоскости на прямой m от точки В отрезок ВВ₁, равный АВ. Сумма углов треугольника АВВ₁ равна 2d. Угол АВВ₁ – прямой, поэтому . По построению - равнобедренный. Отсюда следует, что . Отложим на луче ВВ₁ от точки В₁ отрезок АВ₁. Получим точку В₂ (см. рис. 42). Угол АВ₁В треугольника АВ₁В является внешним углом . В силу нашего предположения, . А, так как треугольник АВ₁В₂ – равнобедренный, то . Следовательно, . Аналогично, откладывая на луче ВВ₁ от точки В₂ отрезок АВ₂, получим равнобедренный треугольник АВ₂В₃, угол В₂АВ₃ которого равен . Отсюда следует, что . Продолжая этот процесс, мы получим, что для любого n существует прямая ВАВ_n, лежащая внутри острого угла, образованного прямыми АВ и h, такая, что