
Metod_MR_sam_rab_Teoret._mekhan._14.03.01_00.00.00
.pdf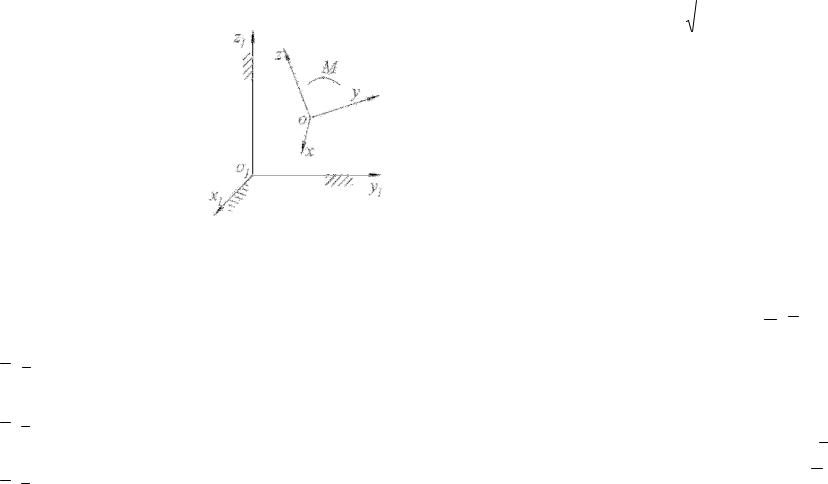
2.5.4 Сложное движение точки
Основные положения кинематики сложного движения точки
Движение точки называется сложным, если точка движется относительно некоторой системы координат оxyz, движущейся относительно другой системы координат о1x1y1z1, условно принимаемой за неподвижную и называемой основной системой отсчёта (рис. 39). Движение точки по отношению к основной системе
отсчёта о1x1y1z1 |
называется |
|
||||
абсолютным |
|
движением. |
|
|||
Движение точки по отношению |
|
|||||
к подвижной |
системе отсчёта |
|
||||
оxyz называется относитель- |
|
|||||
ным. Переносное движение – |
|
|||||
движение |
подвижной системы |
|
||||
отсчёта |
по |
отношению |
к |
|
||
неподвижной. |
|
|
|
|
||
Для того чтобы выделить |
|
|||||
относительное движение точки, |
|
|||||
нужно мысленно |
остановить |
|
||||
подвижную |
систему |
(как |
|
|||
правило, |
твёрдое |
тело) |
и |
Рисунок 39 – Сложное |
||
посмотреть, как при этом будет |
||||||
движение точки |
||||||
двигаться |
|
точка. |
Для |
|||
|
|
|||||
определения переносного движения необходимо мысленно скрепить данную точку с подвижной системой отсчёта (с движущимся твёрдым телом). Движение твёрдого тела с рассматриваемой точкой, как точкой тела, является переносным движением.
Приняты следующие обозначения:
Va , aa – абсолютная скорость и абсолютное ускорение точки
(скорость и ускорение точки по отношению к основной системе отсчёта);
Vr , ar – относительная скорость и относительное ускорение
точки (скорость и ускорение точки по отношению к подвижной системе отсчёта);
Ve , ae – переносная скорость и переносное ускорение (скорость и ускорение точки подвижной системы отсчёта, с которой в данный
61
момент времени совпадает движущаяся точка).
В сложном движении абсолютная скорость точки равна векторной (геометрической) сумме её переносной и относительной скоростей, т.е.:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Va = Ve +Vr . |
|
|
|
|
|
|
|
(47) |
||||||
Величина (модуль) абсолютной скорости находится по формуле: |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V 2 |
+V 2 |
|
|
|
|
|
|
|
|
||
V = |
+ 2V V cos(V ,V |
r |
) . |
(48) |
||||||||||
|
a |
|
e |
|
r |
e r |
e |
|
|
|
||||
Вектор абсолютного ускорения точки равен векторной сумме переносного ускорения, относительного ускорения и ускорения
Кориолиса: |
|
||||||||||||||||||
|
|
|
|
|
|
|
a = |
|
e + |
|
|
r + |
|
|
K , |
(49) |
|||
a |
a |
a |
a |
||||||||||||||||
где |
|
K – ускорение Кориолиса. |
|
||||||||||||||||
a |
|
||||||||||||||||||
|
|
|
Ускорение Кориолиса (добавочное ускорение) определяется по |
||||||||||||||||
формуле: |
|
||||||||||||||||||
|
|
|
|
|
|
K = 2( |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
a |
ωe × Vr ) , |
(50) |
||||||||||||
где |
|
|
движения |
||||||||||||||||
ωe – вектор угловой скорости переносного |
|||||||||||||||||||
(переносная угловая скорость).
Из выражения (50) следует формула для вычисления модуля ускорения Кориолиса, а именно:
|
|
aK = 2ωeVr sin(ωe ,Vr ) . |
(51) |
Направление ускорения Кориолиса определяется по правилу векторного произведения в равенстве (50) или по правилу Н.Е. Жуковского.
Правило Н.Е. Жуковского.
1) Вектор относительной скорости Vr спроецировать на плоскость, перпендикулярную вектору ωe (оси переносного
вращения).
2) Полученную проекцию повернуть в указанной плоскости на
62

угол 90° в сторону переносного вращения – это и будет направление ускорения Кориолиса (рис. 40).
Ускорение Кориолиса равно нулю в следующих случаях:
а) ωe = 0, т.е. в случае переносного поступательного движения; б) ωe Vr – векторы угловой скорости переносного движения и
относительной скорости параллельны;
в) в моменты времени, когда ωe и (или) Vr равны нулю.
Рисунок 40 – Направление ускорения Кориолиса
Если переносным движением является вращение твёрдого тела вокруг неподвижной оси и относительное движение точки криволинейно, то формулу (49) необходимо записывать в следующем виде:
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
n + |
|
τ |
+ |
|
n + |
|
τ + |
|
|
, |
(52) |
|
|
|
|
|
|
|
|
|
|
a |
a |
a |
a |
a |
a |
a |
K |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
e |
|
r |
r |
|
|
|||||||
где |
|
n , |
|
τ |
и |
|
n , |
|
τ |
– нормальные |
|
и |
касательные ускорения |
|||||||||||||
a |
a |
a |
a |
|
||||||||||||||||||||||
|
e e |
|
r r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
соответственно |
в |
переносном |
и |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
относительном движениях. |
|
|
|||||||||||||
Величины этих ускорений определяются по формулам:
an |
= ω |
2h , |
aτ |
= ε |
e |
h |
, |
|
|
|
|
|
|
(53) |
||||
e |
|
|
e |
e |
e |
|
|
e |
|
|
|
|
|
|
|
|
||
|
|
|
|
2 |
|
|
|
|
|
|
|
~ |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
n |
|
Vr |
|
τ |
|
~τ |
|
|
dVr |
|
d |
|
Sr |
|
|
|||
ar |
= |
|
|
|
, |
ar = |
ar |
|
= |
|
|
= |
|
|
|
, |
(54) |
|
|
ρ |
r |
|
|
dt |
dt 2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
где ωe , ε e – угловая скорость |
и |
угловое |
ускорение |
переносного |
||||||||||||||
|
|
|
|
|
|
|
63 |
|
|
|
|
|
|
|
|
|
|
|
вращения;
he – расстояние движущейся точки до оси переносного
|
|
~ |
|
вращения; |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||
~τ |
= |
|
dVr |
|
алгебраическая |
величина |
|
касательного |
||||
ar |
|
|
|
|
– |
|
||||||
|
dt |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
относительного ускорения; |
|
|
|
|||
~ |
= |
dS |
r |
– алгебраическая относительная скорость; |
||||||||
V |
|
|
||||||||||
|
|
|
||||||||||
r |
|
|
dt |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||
S r |
= S r (t) – |
дуговая |
координата |
точки |
в |
относительном |
||||||
|
|
|
|
|
|
|
движении; |
|
|
|
|
|
ρr – радиус |
кривизны |
траектории |
точки |
в |
относительном |
|||||||
|
|
|
движении. |
|
|
|
|
|
||||
Если переносное движение является плоским или имеет место общий случай движения твёрдого тела, то для определения переносного ускорения следует воспользоваться формулой ускорения точки тела в соответствующем движении.
При определении абсолютной скорости и абсолютного ускорения точки по векторным формулам (47) и (49) – (52) обычно применяется метод проекций. Согласно этому методу, необходимо спроецировать, например, равенство (52) на оси выбранной системы координат, т.е. вычислить проекции абсолютного ускорения на эти оси, а именно:
a |
ax |
= a n |
+ aτ |
+ an |
+ aτ |
+ a |
Kx , |
|||||
|
|
ex |
|
ex |
rx |
|
rx |
|
||||
a = an |
+ aτ |
+ an |
+ aτ |
+ a |
Ky |
, |
|
(55) |
||||
ay |
|
|
ey |
|
ey |
ry |
ry |
|
|
|
|
|
a |
az |
= an |
+ aτ |
+ an |
+ aτ |
|
+ a |
Kz . |
||||
|
|
|
ez |
|
ez |
rz |
|
rz |
|
|||
Далее определяется модуль абсолютного ускорения по формуле:
|
|
|
|
a |
a |
= |
a2 + a2 |
+ a2 |
|
|
|
|
|
|
|
|
|
(56) |
|||||||
|
|
|
|
|
|
|
|
ax |
|
ay |
|
az |
|
|
|
|
|
|
|
|
|
|
|||
и вычисляются направляющие косинусы вектора |
|
a : |
|
||||||||||||||||||||||
a |
|
||||||||||||||||||||||||
|
|
|
|
a |
|
|
|
|
|
|
|
aay |
|
|
|
a |
|
|
|
|
|
||||
cos (a |
a |
, x)= |
|
ax |
, cos(a |
a |
, y )= |
, cos (a |
a |
, z )= |
az |
. |
(57) |
||||||||||||
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
aa |
|
|
|||||||||||||||||||
|
|
|
|
aa |
|
|
|
|
|
|
|
|
|
aa |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
64 |
|
|
|
|
|
|
|
|
|
|
|
План решения задач
1)Разложить движение точки на составляющие, определив относительное, переносное и абсолютное движения.
2)Определить положение точки в подвижной системе отсчёта (на твёрдом теле) в расчётный момент времени.
3)Найти относительную скорость и относительное ускорение
точки.
4)Определить в переносном движении угловую скорость, угловое ускорение, скорость и ускорение точки.
5)По найденной угловой переносной скорости и относительной скорости точки определить ускорение Кориолиса.
6)Пользуясь методом проекций, определить модули и направления (в виде направляющих косинусов) абсолютной скорости
иабсолютного ускорения точки.
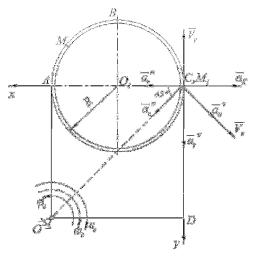
Пример 1. Пластина OABCD (OA = OD, рис. 41) вращается вокруг оси, проходящей через точку О перпендикулярно плоскости
пластины, по закону ϕe = 0,5t 2 − t 3 , рад (положительное направление отсчёта угла ϕe показано на рисунке 41 дуговой стрелкой). По дуге окружности радиусом R=0,5м движется точка М по закону S r = AM = 2πR cos(π t / 3) , м (положительное направление отсчёта дуговой координаты Sr – от А к М). Определить абсолютную скорость и абсолютное ускорение точки в момент времени t1 = 2 с.
65
Рисунок 41 – К примеру 1
Решение:
1) Точка М совершает сложное движение. Относительным движением при этом является движение точки по дуге окружности
радиусом |
R |
в |
соответствии |
с |
уравнением |
S r = AM = 2πR cos(π t / 3) , |
м. Переносное |
движение |
– вращение |
||
пластины OABCD вокруг неподвижной оси, проходящей через точку О перпендикулярно плоскости пластины, по закону ϕe = 0,5t 2 − t 3 ,
рад. Движение точки по отношению к неподвижной плоскости, в которой расположена пластина, является абсолютным.
2) Определяем положение точки М на пластине, для чего вычисляем значение дуговой координаты Sr в заданный момент времени t1 = 2с; численно:
S r1 = AM 1 = 2πR cos(2π / 3) = 2πR(−0,5) = −πR м.
На рисунке 41 показано положение точки М1, соответствующее вычисленному значению дуговой координаты, т.к.:
AO1M 1 = S r1 / R = −π .
3) Находим относительную скорость точки, алгебраическое значение которой равно:
66

|
|
|
|
|
~ |
= |
dS |
r |
= − |
2 |
π 2 R sin(π t / 3) . |
|
||||
|
|
|
|
|
V |
|
|
(58) |
||||||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
r |
|
dt |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Для момента t1 = 2 с, учитывая, что R = 0,5 м, получим |
||||||||||||||||
~ |
= − |
2 |
π |
2 |
R sin(2π |
/ 3) = − |
2 |
3,14 |
2 |
0,5 0,87 |
= −2,86 м/с . |
|||||
Vr |
|
|
|
|
||||||||||||
3 |
|
3 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Знак "–" показывает, что вектор относительной скорости Vr направлен по касательной к окружности в сторону отрицательного
отсчёта дуговой координаты |
|
|
Sr |
|
(рис. |
41). Модуль относительной |
||||||||||||||||||||
скорости равен: |
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
Vr = |
|
|
= 2,86 м/с. |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
Vr |
|
|
|
|
|
||||||||||
|
|
Далее определяем относительное ускорение точки: |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
n + |
|
τ |
, |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
a |
r |
|
a |
a |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
r |
|
|
|
|
|
||
где |
|
n , |
|
τ – |
нормальное |
|
и касательное |
относительные ускорения, |
||||||||||||||||||
a |
a |
|||||||||||||||||||||||||
|
r r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
вычисляемые по формулам (54). |
|
|
|
|
|||||||||||||||||
|
|
Имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
n |
|
Vr2 |
|
2,862 |
|
|
|
|
|
2 |
|
|
|
τ |
|
~τ |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
ar |
= |
|
|
= |
|
|
= 16,36 м/с |
, |
|
ar |
= |
ar |
|
. |
|||||||||
|
|
|
ρr |
0,5 |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Вектор |
|
n |
направлен к центру окружности (рис. 41). Находим |
|||||||||||||||||||||
|
|
a |
||||||||||||||||||||||||
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
алгебраическую величину касательного относительного ускорения. Учитывая выражение (58), получаем:
~τ |
= |
dVr |
= |
d 2 Sr |
= − |
2 |
π |
3 |
R cos(π t / 3) . |
ar |
|
|
|
|
|||||
dt |
dt 2 |
9 |
|
||||||
|
|
|
|
|
|
|
Для момента времени t1 = 2 c имеем:
~τ |
= − |
2 |
π |
3 |
R cos(2π / 3) |
= − |
2 |
3,14 |
3 |
0,5 (−0,5) = 1,72 м/с |
2 |
ar |
|
|
|
|
|
||||||
9 |
|
9 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
~ |
|
Положительное значение |
τ |
означает, что вектор |
ar |
относительного касательного ускорения arτ направлен по касательной
к окружности в положительном |
|
направлении. Модуль вектора |
|
τ |
|||||
a |
|||||||||
|
|
|
|
|
|
|
|
r |
|
равен: |
|
|
|
|
|
|
|
|
|
τ |
= |
|
~τ |
|
= |
2 |
|
|
|
|
|
|
|
|
|||||
ar |
|
ar |
|
1,72 м/с |
. |
|
|
||
|
|
|
|
67 |
|
|
|
|
|
4) Определяем в переносном движении угловую скорость и угловое ускорение, а также переносную скорость и переносное ускорение точки.
Алгебраические значения переносной угловой скорости и переносного углового ускорения равны:
~ |
|
dϕe |
|
2 |
|
~ |
|
dωe |
|
d 2ϕe |
|
|
ωe |
= |
|
= t − 3t |
|
, |
ε e |
= |
|
= |
|
= 1 |
− 6t . |
dt |
|
dt |
dt 2 |
|||||||||
|
|
|
|
|
|
|
|
|
|
Для момента времени t1 = 2 c получаем:
~ |
= 2 − 3 2 |
2 |
|
= −10рад/с, |
~ |
= 1− 6 2 = −11рад/с |
2 |
||||||||
ωe |
|
|
ε e |
. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Модули этих величин равны: |
|
|
|
|
|
|
|
|
|
||||||
|
ωe = |
|
~ |
|
= 10 рад/ с, |
ε e |
= |
|
~ |
|
= 11рад/с |
2 |
. |
|
|
|
|
|
|
|
|
||||||||||
|
|
ωe |
|
|
ε e |
|
|
|
|||||||
|
|
|
|
|
~ |
~ |
|
|
|
|
|
|
|
|
|
Отрицательные значения ωe и |
εe показывают, что переносные |
||||||||||||||
угловая скорость и угловое ускорение направлены противоположно положительному направлению отсчёта угла поворота пластины ϕe
(рис. 41). Вектор переносной угловой скорости ωe направлен по оси вращения пластины от нас (с конца вектора ωe вращение тела должно
наблюдаться происходящим против хода часовой стрелки).
Находим переносную скорость точки во вращательном движении пластины с угловой скоростью ωe . Имеем:
Ve = ωe he = 10 1,41 = 14,1м/с,
где he = ОМ1 = 2R
 2 = 2 0,5 1,41 = 1,41м – расстояние от точки М1 до оси вращения О (рис. 41).
2 = 2 0,5 1,41 = 1,41м – расстояние от точки М1 до оси вращения О (рис. 41).
|
|
|
направлен перпендикулярно ОМ1 в сторону угловой |
Вектор Ve |
|
||
|
|
|
скорости ωe (рис. 41). |
Определяем переносное ускорение точки в рассматриваемом движении пластины. Учитывая формулы (53), получим:
|
|
|
|
|
|
= |
|
n + |
|
τ |
, |
|
|
|
|
a |
a |
a |
|
||||||
|
|
|
|
е |
|
е |
е |
|
|
|||
где |
a n = ω 2 h = 102 |
1,41 = 141м/с2 – |
|
нормальное |
переносное |
|||||||
|
e |
e e |
|
|
|
|
|
|
|
|
|
|
ускорение;
68
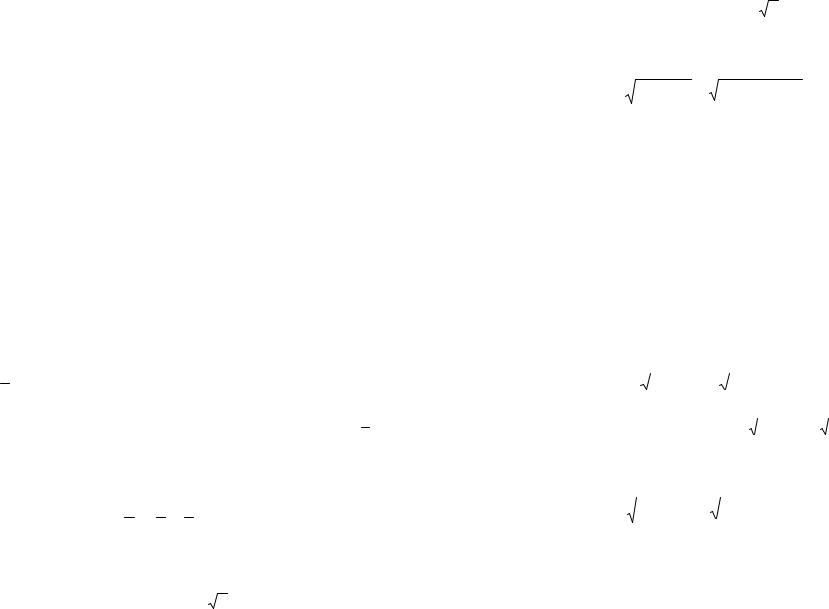
aτ |
= ε |
h |
= 11 1,41 = 15,51м/с2 – |
касательное |
переносное |
|||||||||||||||||||||
e |
|
|
|
e e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ускорение. |
|
|||||||
Вектор |
|
|
n |
– |
направлен к оси вращения пластины, |
|
||||||||||||||||||||
a |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вектор |
|
|
τ |
– |
перпендикулярно |
ОМ1 в |
|
|
сторону |
углового |
||||||||||||||||
a |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
ускорения εe (рис. 41). |
|
|
|
|
|
||||||||||
5) |
Находим |
|
|
ускорение Кориолиса. |
Модуль |
ускорения |
||||||||||||||||||||
Кориолиса определяем по формуле (51): |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
aK = 2ωeVr sin( |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωe ,Vr ) , |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где ( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
угол между вектором |
|
|
|
|
вращения |
||||||
ωe ,Vr ) = 90° – |
ωe (осью |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
пластины), |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
(ось |
вращения |
перпендикулярно |
плоскости |
||||||||||||||||||
и вектором Vr |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
пластины, в которой расположен вектор |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
относительной скорости Vr |
). |
|
|||||||||
Численно: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
K |
= 2 10 2,86 = 57,2 м/с2. |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Направление |
|
K |
находим по правилу Н.Е. Жуковского: так как |
|||||||||||||||||||||||
a |
||||||||||||||||||||||||||
вектор Vr находится в плоскости, перпендикулярной оси вращения, то поворачиваем его на 90° в этой же плоскости в сторону угловой скорости ωe , т.е. по ходу часовой стрелки. Изображаем вектор aK на рисунке 41.
6) Определяем абсолютную скорость точки в соответствии с
векторной формулой (47), т.е.: |
|
Va = Ve + Vr . |
(59) |
Проецируем равенство (59) на координатные оси M1x и M1y (рис. 41). Получим для момента времени t1 = 2 с:
V |
|
= −V |
cos 45° = −14,1 |
2 |
= −9,97 м/с; |
ax |
|
||||
|
e |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
69 |
|
|
V |
|
= V cos 45° − V |
|
= 14,1 |
2 |
− 2,86 = 7,11м/с. |
ay |
r |
|
||||
|
e |
|
2 |
|
||
|
|
|
|
|
|
|
По вычисленным проекциям находим модуль абсолютной |
||||||
скорости: |
|
|
|
|
|
|
V = |
V 2 + V 2 = |
9,972 + 7,112 = 12,25 м/с. |
|
|||||||||||||||||||||||
a |
ax |
|
ay |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Определяем направляющие косинусы вектора Va |
: |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
Vax |
|
|
|
|
9,97 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
, x) = |
|
= − |
|
|
|
|
|
|
|||||||||||||
|
cos (V |
|
= −0,81 |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
a |
|
|
|
|
Va |
12,25 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Vay |
|
|
7,11 |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
, y) = |
= |
|
|
|
|
|
|
|
|
||||||||||||
|
cos(V |
|
= 0,58 |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
a |
|
|
|
|
Va |
12,25 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Далее находим абсолютное ускорение точки при помощи |
||||||||||||||||||||||||||
формулы (52). Имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
= |
|
n |
+ |
|
τ + |
|
n + |
|
τ + |
|
|
|
|
(60) |
|||||||
|
|
a |
a |
a |
a |
a |
a |
a |
K |
|||||||||||||||||
|
|
|
|
|
|
|
|
e |
|
|
|
e |
|
r |
|
r |
|
|||||||||
Спроецируем обе части (60) на оси M1x и M1y. Получим для t1 = 2 c:
|
|
|
|
|
|
|
a |
ax |
= a n cos 45° − aτ cos 45° + an |
|
− a |
K |
= |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
e |
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
= 141 |
|
|
2 |
− 15,51 |
|
|
2 |
+ 16,36 − 57,2 = 47,88 м/с2; |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
a |
= an cos45° + aτ |
cos45° + aτ = 141 |
|
2 |
+15,51 |
|
|
2 |
+1,72 = 112,37м/с2. |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
ay |
|
e |
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
r |
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Теперь вычисляем модуль абсолютного ускорения в заданный |
|||||||||||||||||||||||||||||||||||||||
момент времени t1 = 2 с: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
aa |
|
= |
|
|
aax2 + aay2 = |
|
47,882 + 112,372 = 122,15м/с2. |
|
|||||||||||||||||||||||||||
|
Определяем |
|
направление |
|
|
вектора |
|
|
|
a |
|
через направляющие |
||||||||||||||||||||||||||||
|
|
|
|
|
a |
|
||||||||||||||||||||||||||||||||||
косинусы; численно: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
a |
|
|
|
|
47,88 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
aay |
|
112,37 |
|
|
|||||||||||
cos ( |
|
|
, x) = |
ax |
= |
= 0,39 cos( |
|
|
|
, y) = |
= |
= 0,92 |
|
|||||||||||||||||||||||||||
a |
a |
|
|
|
|
|
|
|
a |
a |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
122,15 |
|
aa |
122,15 |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
aa |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Ответ: |
|
|
|
V |
|
= 12,25 см/с, |
|
|
|
|
|
|
|
|
|
a |
a |
= 122,15 см/с2. |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
70 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
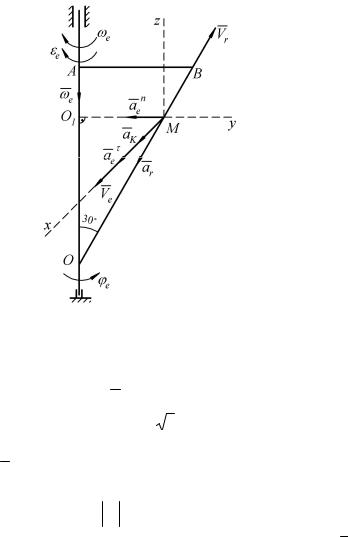
Пример 2. Пластина ОАВ вращается вокруг неподвижной оси ОА по закону ϕe = 0,9t 2 − 9t 3 (положительное направление отсчёта угла поворота ϕe показано на рис. 42). По прямой ОВ движется точка
М согласно |
уравнению S r = ОM = 16 − 8cos 3π t |
(положительное |
направление |
отсчёта координаты Sr – от О к |
В). Определить |
абсолютную скорость и абсолютное ускорение точки М для момента
времени t = |
2 |
c ( ϕ |
|
– в рад., S |
|
– в см). |
|
9 |
e |
r |
|||||
|
|
|
|
||||
|
|
|
|
|
|
Решение:
1) Точка М совершает сложное движение. Относительное движение – движение точки М по прямой ОВ по
закону S r = ОM = 16 − 8cos 3π t ,см. Переносное движение – вращение
пластины |
ОАВ |
|
вокруг |
|
неподвижной оси |
ОА по |
закону |
|||||||
ϕ |
e |
= 0,9t 2 |
− 9t 3 , рад. Абсолютным движением |
является движение |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
точки М по отношению к неподвижной стойке. |
|
|
||||||||||||
|
|
2) Определяем положение точки М на пластине по значению |
||||||||||||
координаты Sr , вычисленному |
для заданного |
момента |
времени. |
|||||||||||
Имеем при t = = |
2 |
с: |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
= 16 − 8cos |
2 |
π = 16 − 8 (−0,5) |
= 20 см. |
|
||||
|
|
|
|
r |
|
|
|
|||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
На рисунке 42 показано положение точки М, в котором ОМ = |
||||||||||||
20см. |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
3) Находим относительную скорость точки, алгебраическая |
||||||||||||
величина которой равна: |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
~ |
|
dS r |
& |
|
|
||
|
|
|
|
|
|
|
Vr |
= |
|
|
|
= S r = 24π sin 3π t . |
|
|
|
|
|
|
|
|
|
dt |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
71
Рисунок 42 – К примеру 2
Для момента времени t = 2 с получим:
9
~ |
= 24π sin |
2 |
π = 24π |
3 |
= 65,22 |
см/с. |
|
Vr |
|
|
|||||
3 |
2 |
||||||
|
|
|
|
|
~
Вектор Vr направлен в положительном направлении, т.к. Vr > 0 (рис. 42). Модуль относительной скорости равен:
~
Vr = Vr = 65,22 м/с.
Определяем относительное ускорение точки в виде вектора ar , направленного по прямой относительного движения. Вычисляем
сначала алгебраическое значение |
~ |
|
|
2 |
|
||||
ar |
для t = |
|
с, а именно: |
||||||
|
|||||||||
|
|
~ |
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
dVr |
&& |
|
|
2 |
|
|
|
ar |
= |
|
= Sr = 72π |
|
cos3π t |
||||
dt |
|
||||||||
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
72 |
|
|
|
|
|
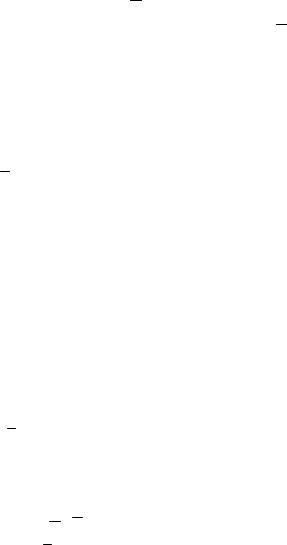
для t = |
2 |
с получаем: |
|
|
|
|
|
|
|
|
|
||||||||
9 |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
2 |
2 |
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
ar |
= 72π |
|
cos |
|
π = 72π |
|
(−0,5) |
= −355,31 |
см/с |
. |
|||||||||
|
|
|
|||||||||||||||||
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Вектор |
|
|
|
r |
направлен |
|
по |
|
прямой |
|
ОВ в |
отрицательном |
|||||||
|
a |
|
|
||||||||||||||||
направлении (рис. 42), так как |
|
~ |
|
Модуль |
относительного |
||||||||||||||
|
ar < 0 . |
|
|||||||||||||||||
ускорения равен: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
ar |
= |
|
~ |
|
= |
|
|
|
2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
ar |
|
355,31м/с |
|
|
||||||||
4) Определяем в переносном вращении угловую скорость и угловое ускорение. Алгебраическое значение переносной угловой скорости равно:
~ |
dϕe |
|
|
|
& |
|
|
|
|
|
2 |
||||||
|
|
ωe = |
|
|
|
|
|
= |
|
= 1,8t − 27t ; |
|||||||
|
|
|
dt |
ϕe |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
для t = |
2 |
c получаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
2 |
|
|
|
|
|
|
|
|
4 |
|
|
рад/с . |
||||
|
|
ωe = 1,8 |
|
|
− 27 |
|
|
|
= −0,93 |
||||||||
|
|
9 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
81 |
|
|
|
|||||
Модуль переносной угловой скорости равен: |
|||||||||||||||||
|
|
ωe |
|
= |
|
~ |
|
|
= 0,93 рад/с |
|
|
||||||
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
ωe |
|
|
. |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Аналогично находим алгебраическое значение и модуль |
|||||||||||||||||
переносного углового ускорения: |
|
|
|
|
|
|
|
||||||||||
~~&
εe = ωe = ϕ&&e = 1,8 − 54t ;
численно при t = |
|
2 |
c: |
|
|
|
|
9 |
|
|
|
|
|||
|
|
|
|
|
|
||
~ |
= 1,8 − 54 |
2 |
= −10,2 рад/с |
2 |
|
||
ε e |
|
|
; |
||||
9 |
|
||||||
|
|
|
|
|
|
|
|
Модуль переносного углового ускорения равен:
ε e = |
|
~ |
|
2 |
|
|
|||
|
ε e |
|
= 10,2 рад/с . |
Переносные угловая скорость и угловое ускорение в заданный момент времени направлены противоположно положительному
~ |
< 0 |
~ |
< 0 . Вектор |
отсчёту угла поворота пластины ϕe , так как ωe |
и ε e |
||
73 |
|
|
|
переносной угловой скорости ωe направлен по оси вращения пластины от А к О (рис. 42), поскольку с конца вектора ωe вращение
пластины наблюдается происходящим против хода часовой стрелки. Далее находим переносную скорость точки во вращательном
движении пластины с угловой скоростью ωe :
Ve = ωe he = 0,93 10 = 9,3 см/с,
где he = О1М = ОМ sin 30° = 20 0,5 = 10 см – расстояние от точки М до оси переносного вращения.
Вектор Ve направлен перпендикулярно плоскости пластины в сторону угловой скорости ωe (рис. 42).
Определяем переносное ускорение точки в рассматриваемом движении пластины:
|
|
|
|
|
|
|
|
|
= |
|
n + |
|
τ |
, |
|
||
|
|
|
|
|
|
|
a |
a |
a |
|
|||||||
|
|
|
|
|
|
|
|
е |
|
е |
|
е |
|
|
|||
где |
an = ω |
2 h |
= 0,932 10 = 8,65 см/с2 |
– нормальное |
переносное |
||||||||||||
|
e |
|
e |
e |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
ускорение; |
|
|
|
|
|
|
|
|
||
|
aτ |
= ε |
h |
= 10,2 10 = 102 |
см/с2 |
|
|
– |
касательное |
переносное |
|||||||
|
e |
|
e |
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ускорение. |
|
|
|
|
|
|
|
|
||
|
Вектор |
|
|
n |
направлен |
по |
перпендикуляру МО1 к оси |
||||||||||
|
a |
||||||||||||||||
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
вращения,
а вектор aeτ – перпендикулярно плоскости пластины в сторону углового ускорения εe (рис. 42).
5) Определяем ускорение Кориолиса, модуль которого равен:
aK = 2ωeVr sin(ωe ,Vr ) = 2 0,93 65,22 sin150° = 60,65 см/с2.
Направление aK находим по правилу Н.Е. Жуковского. В
соответствии с этим правилом (см. выше) вектор ускорения Кориолиса направлен перпендикулярно плоскости пластины в сторону угловой
скорости ωe (рис. 42).
74

6) Определяем абсолютную скорость точки:
Va = Ve + Vr .
Вычисляем модуль абсолютной скорости, учитывая, что векторы
Ve и Vr взаимноперпендикулярны:
Va = 
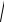 Ve2 + Vr2 =
Ve2 + Vr2 = 
 9,32 + 65,222 = 65,88 см/с.
9,32 + 65,222 = 65,88 см/с.
Далее методом проекций определяем абсолютное ускорение точки. Для этого выберем оси координат Мx, My, Mz как показано на рисунке 42 (ось Mx направлена перпендикулярно плоскости пластины, а оси My и Mz расположены в этой плоскости). Вектор абсолютного ускорения равен:
|
|
|
= |
|
n + |
|
τ |
+ |
|
|
+ |
|
|
|
|
a |
a |
a |
a |
a |
r |
a |
K , |
|
|||||||
|
|
|
e |
e |
|
|
|
|
|
||||||
где модули всех ускорений в правой части этой формулы для t = |
2 |
с |
|||||||||||||
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
определены выше.
Спроецируем обе части этого выражения на оси координат. Получаем:
aax = aτe + aK = 102 + 60,65 = 162,65 см/с2,
aay = −aen − ar cos60° = −8,65 − 355,31 0,5 = −186,30 см/с2,
aaz = −ar cos30° = −355,31 0,87 = −309,12 см/с2.
Модуль абсолютного ускорения равен:
a |
a |
= |
|
a 2 |
+ a |
2 |
+ a 2 |
= 162,622 + 186,32 + 309,122 |
= 395,88 см/с2. |
|||||||||||||||||||||||
|
|
|
|
ax |
|
|
ay |
|
|
az |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
Вычисляем направляющие косинусы вектора |
|
a : |
|
|||||||||||||||||||||||||
|
|
|
|
a |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
a |
|
|
|
|
162,65 |
|
|
|
|
|
|
|
|
|
aay |
|
|
|
186,3 |
|
||||||
cos ( |
a |
a |
, x)= |
|
|
ax |
|
= |
|
|
|
|
|
= 0,41 |
; |
cos( |
a |
a |
, y ) |
= |
|
= − |
|
= −0,47 ; |
||||||||
|
aa |
|
395,88 |
aa |
395,88 |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
aaz |
|
|
309,12 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
cos ( |
|
|
, z )= |
|
= − |
= −0,78 . |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
a |
a |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
aa |
|
395,88 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
Ответ: |
|
V |
|
= 65,88 см/с, |
|
|
|
|
|
a |
a |
= 395,88 см/с2. |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
75 |
|
|
|
|
|
|
|
|
|
|
|
|
Список литературы
1.Бутенин, Н. В. Курс теоретической механики [Текст]: учебник / Н. В. Бутенин, Н. Л. Лунц, Л. Р. Меркин. – Санкт- Петербург : Лань, 2004. – 736 с.
2.Митюшов, Е. А. Теоретическая механика [Текст] / Е. А. Митюшов, С. А. Берестова. – Москва : Академия, 2001. - 318 с.
3.Тарг, С. М. Краткий курс теоретической механики [Текст] : учеб. для втузов / С. М. Тарг. – 12-е изд., стер. – Москва :
Высш. шк., 2002. – 416 с.
4.Статика [Текст] : методические указания к выполнению индивидуальных домашних заданий по теоретической механике / сост. : В. А. Нарыжный, С. Ф. Годунов. – Новочеркасск : ЮРГТУ, 2004. - 30 с.
5.Кинематика [Текст] : методические указания к выполнению индивидуальных домашних заданий по теоретической механике / сост. : В. А. Нарыжный, С. Ф. Годунов. – Новочеркасск : ЮРГТУ, 2007. - 50 с.
6.Нарыжный, В. А. Динамика [Текст] : учеб. пособие по теоретической механике. – Москва : НИЯУ МИФИ, 2012. – 168 с.
7.Бать М. И.Теоретическая механика в примерах и задачах [Текст] : учеб. пособие / М. И. Бать, Г. Ю. Джанелидзе, А. С. Кельзон. – Санкт-Петербург : Лань, 2010.
8.Программное обеспечение и Интернет – ресурсы. – Режим доступа: www.teoretmex.ru
76
Приложение А
(справочное)
Пример выполнение титульного листа
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«Национальный исследовательский ядерный университет «МИФИ» Волгодонский инженерно-технический институт – филиал НИЯУ МИФИ
Индивидуальное домашнее задание
по дисциплине: «Теоретическая механика»
Вариант № ____
Выполнил студент ____________________________________________
(группа, Ф.И.О.)
Проверил _____________________________________________________
(звание, должность, Ф.И.О.)
Волгодонск 20___
77
СТАТИКА, КИНЕМАТИКА
Индивидуальные контрольные задания по теоретической механике
Учебно-методическое пособие
Составители – Пинчук Э.В., Литвинова Т.А.
Компьютерная вёрстка Вишнева М.М. Корректор Вишнева М.М. ИПО ВИТИ НИЯУ МИФИ
Подписано к печати 07.05.2014 г.
Бумага «SvetoCopy» 80 г/м2. Объем 4.56 усл.печ.л. Гарнитура «Times New Roman»,
Тираж 40 экз.
Отпечатано в типографии ИПО ВИТИ НИЯУ МИФИ г. Волгодонск, ул. Ленина, 73/94
78
