Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский университет «Высшая школа экономики»

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Сборник задач по высшей математике

.pdf

Скачиваний:

324

Добавлен:

26.03.2016

Размер:

1.04 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 1314 / 1814 15 16 17 18 > Следующая >>>

Глава

Двойной интеграл

Справочный материал

ипримеры решения задач

1.Если функция z = f (x, y) непрерывна в области интегрирования G, ограниченной прямыми x =a, x =b (a <b) и графиками

непрерывных функций y =ϕ1(x) и y =ϕ2(x), ϕ1(x) ¶ϕ2(x),

то двойной интеграл от функции f (x, y) по области G вычисляется повторным интегрированием по формуле:

RRG	b	ϕ2(x)
RRG	f (x, y) dx dy = Ra	dxϕ1R(x)	f (x, y) dy.

2. Если функция z = f (x, y) непрерывна в области интегрирования G, ограниченной прямыми y =a, y =b (a <b) и графиками

	III. Функции нескольких переменных

непрерывных функций x =g1( y) и x =g2( y), g1( y) ¶g2( y),

то двойной интеграл от функции f (x, y) по области G вычисляется повторным интегрированием по формуле:

		RRG				b	g2( y)
		RRG	f (x, y) dx dy = Ra				dy g1R( y)		f (x, y) dx.
	1.		интеграл					+		по области
Задача		Вычислите		=	x и y	=RRG 2(x			2 y) dx dy		G,
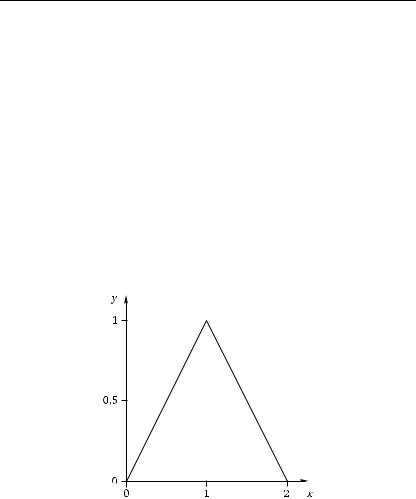
ограниченной линиями y					x и y		2x −x.

Изобразим область интегрирования на плоскости xOy:

Глава . Двойной интеграл

Видно, что данный двойной интеграл следует вычислять первым методом. Тогда

R−

y=x

(x +2 y)dxdy =

2x2

x (x +2 y) dy =

dx(xy+y2) y=2x2

−x

= (

2 +

)

)2)

R0 (−4x

3 +2

−x

−

−x

dx11

= −5 +2 +3

= 30 .

Задача 2. Вычислите интеграл

(2x + 1) dx dy по области G,

−

x и y =0.

ограниченной линиями y =x и y =RR2

Изобразим область интегрирования на плоскости xOy:

Если для вычисления двойного интеграла применить первый метод повторного интегрирования, то получим что

RRG	(2x +1) dx dy = R0	dx R0	(2x +1)dy +R1	dx	R0 (2x +1) dy.
	1	x	2		2−x

Такой метод расстановки пределов интегрирования приводит к необходимости проводить повторное интегрирование дважды. Поэтому в данном случае воспользуемся вторым методом повторного интегри-

		III. Функции нескольких переменных

рования:
RR		1	2−y	1
RR		R	y	R	x=y−	=
G	(2x +1) dx dy = 0 dy		Z (2x +1) dx = 0 dy(x2 +x)		x=y−	=
					x=2	y
	1		1
	= R0	((2 −y)2 +2 −y −y2 −y) dy = R0		(−6 y +6) dy = −3 +6 = 3.

§ . Двойной интеграл

Изобразите область интегрирования на плоскости. Измените порядок интегрирования в повторном интеграле ( . –– . ).

−R0

−R9

1−x

1.1.

f (x, y) dy +

f (x, y) dy.

1.2. −R3 dy yR2

f (x, y) dx +R0

3Ry

f (x, y) dx.

x+1

1.3. −R1 dx

f (x, y) dy +R0

dx xR3

f (x, y) dy.

1.4. −R1 dy

−2Ry−2

f (x, y) dx +R0

dy−p

R4−y2

f (x, y) dx.

−y

1.5. −R1 dy

−R31

f (x, y) dx+R0

dy −R1

f (x, y) dx.

2−y

1.6.

f (x,

y) dx+

f (x, y) dx.

1.7. −R4 dy pR−y

f (x, y) dx+R0

dy Ry

f (x, y) dx.

1−x

1−x2

1.8. Rdx

f (x, y) dy+Rdx

f (x, y) dy.

−1

Глава . Двойной интеграл

6−x

1.9. R0

dx R0 f (x, y) dy +R4

f (x, y) dy.

y+1

1.10. −R1 dy −pRy+1

f (x, y) dx+R0

2−pR9−y2

f (x, y) dx.

1.11. R0

dx−Rp

f (x, y) dy +R1

dx xR−2

f (x, y) dy.

Изобразите область интегрирования на плоскости. Измените порядок интегрирования и найдите интеграл ( . –– . ).

1.12. R0

dy yR/2

f ′(x2) dx +R2

dy yR/2

f ′(x2) dx.

2/y

1.13.

1R/2 dy

1R/y

f ′(ln x) dx +R1

dy R1

f ′(ln x) dx.

Вычислите интеграл

f (x, y) dx dy по области D, ограничен-

ной заданными линиямиRR( . –– . ).

x dx dy; D : y =p

, y =x.

1.14.

1.15. RRD

2 y dx dy; D : y =−x3, y =1, x =0.

; D : y =ln x, y =−xe +2, y =2.

1.16. RR

dx dy

RRy2

1.17.x2 dx dy; y =x, xy =1, y =2.

RRD

1.18.(x −y) dx dy; y =2 −x2, y =2x −1.

RRD

1.19.(x + y) dx dy; x =0, y =0, x + y =2.

RRD

1.20. x2 y dx dy; y =x, x + y =2, x =0.

III. Функции нескольких переменных

1.21.(2 y3 −x) dx dy; y =x +2, x =0, y =0.

DRR

Изобразите область D и найдите интеграл f (x, y) dx dy. Объ-

ясните совпадение ответов в п. а) и б) ( . –– . ).

1.22. (x, y) =4x +1

а) D = 0 ¶x ¶3; 0 ¶y ¶x2 ;

б) D =f 0 ¶y ¶9; p

¶x ¶3 .

1.23. f (x, y) =15 y

а) D = 0 ¶x ¶1; x2

−

1 ¶y ¶0 ;

−

б) D = 1 ¶y ¶0; 0 ¶x ¶ y +1 .

1.24. f (−x, y) =5 y а) D ={0p¶x ¶3, x ¶y ¶x2};

−

9, p

¶x ¶3}.

б) D ={

3 ¶y ¶0,

y ¶x ¶3}

{0 ¶y ¶

1.25. f (x, y) =2x + y а) область D ограничена линиями x =3 y, x =0, y =1;

б) область D ограничена линиями y =3x, y =0, x =1.

1.26. а) Область D ограничена линиями x = 6 y, x = 0, y = 1; f (x, y) =x +2 y;

б) область D ограничена линиями y =6x, y =0, x =1; f (x, y) =

=2x + y.

Найдите интеграл f (x, y) dx dy. Сравните результат с объе-

мом соответствующего тела ( . –– . ).

1.27.D ={0 ¶x ¶2; 0 ¶y ¶1}, f (x, y) =3.

1.28.D ={0 ¶x ¶2; 0 ¶y ¶x}, f (x, y) =3.

1.29.D ={0 ¶x ¶2; 0 ¶y ¶x}, f (x, y) =3 y.

1.30.D ={0 ¶x ¶2; 0 ¶y ¶x}, f (x, y) =3x.

1.31.D ={0 ¶x ¶2; −x ¶y ¶x}, f (x, y) =3 y.

1.32.D ={0 ¶x ¶2, −x ¶y ¶x}, f (x, y) =3x.

1.33.D ={0 ¶x ¶1; 0 ¶y ¶1 −x}, f (x, y) =6x.

1.34.D ={0 ¶x ¶1; 0 ¶y ¶1 −x}, f (x, y) =6 y.

1.35.D ={0 ¶x ¶1; 0 ¶y ¶1 −x}, f (x, y) =6(1 −x −y).

1.36.D ={0 ¶x ¶1; x −1 ¶y ¶1 −x}, f (x, y) =6x.

1.37.D ={0 ¶x ¶1; x −1 ¶y ¶1 −x}, f (x, y) =6 y.

1.38.D ={0 ¶x ¶1; x −1 ¶y ¶1 −x}, f (x, y) =6(1 −x −y).

Ответы к главе

	R1	1R−y
1.1.	dy			f (x, y) dx.
	0	−y
	R1	R3p
	R1	R3p	y
1.3.	dy			f (x, y) dx.
	0	y−1
	0	−x
1.5.	Rdx R f (x, y) dy.
	−1	x3

R2 Rx

1.7.

f (x, y) dy.

0−x2

R2 6R−y

1.9.	dy	f (x, y) dx.
	0	y2

R2 yR+2

1.11.

f (x, y) dx.

1.2. R0

−Rp

f (x, y) dy.

4−x2

1.4. −R2 dx−x/R2−1

f (x, y) dy.

1.6. R1 dx

2R−x f (x, y) dy.

1−y

1.8. R0

−p

R1−y2

f (x, y) dx.

5−x2+4x

1.10. −R1 dx

x2R−1

f (x, y) dy.

−1 y2

R2 R2x

1.12. 12 ( f (4) − f (0)) = dx f ′(x2) dy.

R2 2R/x

1.13.	f (ln 2) − f (0) =				dx			f ′(ln x) dy.
				1			1/x
1.14.	1	.		1.15.		6	.	1.16.	1		−2 ln 2.	1.17.	9		.
	15					7			2				4
1.18.	64		.	1.19.		8	.	1.20.		1	.	1.21.		68		.

	15				3				6				15
1.22. .				1.23.	−4.			1.24. .				1.25. .
1.26. .				1.27.	.			1.28. .				1.29. .
1.30. .				1.31.	.			1.32. .				1.33. .
1.34. .				1.35.	.			1.36. .				1.37. .					1.38. .

Глава

Варианты контрольных работ

Контрольная работа

Вариант

1.Найдите длину проекции вектора ~a =(−2; 3; −1; 4) на вектор

~b =(1; 0; 2; 2).

2.Решите систему линейных уравнений и запишите общее ре-

шение этой системы в векторном виде:

x1 +2x2 −x3 +4x4 = −7,

2x1 +4x2 −2x3 +7x4 = −12, x1 +2x2 −x3 +3x4 = −5.

3.При каком значении параметра a точки A(1; 3; 1), B(2; 3; 0), C(−1; 2; 1) и D(a + 2; 4; 0) лежат в одной плоскости? (Исследуйте линейную зависимость или независимость векторов.)

4.Решите матричное уравнение

−2	−3 X =	5	−12	−8 .
2	1	1	4	4

5.Вычислите алгебраическое дополнение A23 матрицы

A =	−5	0	0	5
A =	3	4	2	1 .
	3	0	1	2
	2	0	0	2

6.Найдите координаты точки, симметричной точке P(−1; 2; 0) относительно плоскости 4x −5 y −z −7 =0.

7.При каком значении параметра a матрица

a		11	4	−2
		+	1	2
	−2		2	1

имеет собственный вектор ~v =(−3; 1; a −1)?

Глава . Варианты контрольных работ

Вариант

1.Найдите cos(~ac, ~b), если |~a|=3, |~b|=5, |~a +~b|=6.

2.Решите систему линейных уравнений и запишите общее решение этой системы в векторном виде:

x1 −3x2 −2x3 +x4 = −6,

2x1 −6x2 −2x3 +2x4 = −4, x1 −3x2 −x3 +x4 = −2.

3. При каком значении параметра a точки A(0; 3; −1), B(2; 8; 7), C(1; 0; 4 −a) и D(0; 8; 9) лежат в одной плоскости? (Исследуйте линейную зависимость или независимость векторов.)

4. Решите матричное уравнение

X	·	−3	−	6	= −1 −4 .
	·		−			3	9
		2		5	−	2	5
					−

5. Вычислите минор M32 матрицы

−4		−2	1	2
	2	3	0	0

A= .

2 3 2 4

0 1 3 2

6.Найдите координаты точки, симметричной точке P(2; −1; 1) относительно плоскости x −y +2z −2 =0.

7.При каком значении параметра a матрица

2	1	−1
a −4	3	−1

0−1 3

имеет собственный вектор ~v =(2; 3; a −1)?

Вариант

1. Найдите длину проекции вектора ~a = (1; 2; 5; 1) на вектор

~b =(2; 1; 0; −2).

	III. Функции нескольких переменных

2. Решите систему линейных уравнений и запишите общее ре-

шение этой системы в векторном виде:

x1 −x2 +2x3 +3x4 = 10,

2x1 −2x2 +4x3 +3x4 = 11, x1 −x2 +2x3 +2x4 = 7.

3.При каком значении параметра a точки A(1; 2; 1), B(3; 6; 4), C(5; 9; a +3) и D(3; 2; 0) лежат в одной плоскости? (Исследуйте линейную зависимость или независимость векторов.)

4.Решите матричное уравнение

−2	4 X	6	6	−−8 .
−3	5	= 7	8	10

5.Вычислите алгебраическое дополнение A43 матрицы

A =		0	2	4	0
A =	−4		3	3	0 .
		2	0	2	2

31 −5 −2

6.Найдите координаты точки, симметричной точке P(1; 1; 1) относительно плоскости x +4 y +3z +5 =0.

7.При каком значении параметра a матрица

4	0	−1
a−−11	0	4
	2	1

имеет собственный вектор ~v =(1; 3; a −2)?

Вариант

1.Найдите cos(~ac, ~b), если |~a|=4, |~b|=3 и |~a −~b|=2.

2.Решите систему линейных уравнений и запишите общее ре-

шение этой системы в векторном виде:

x1 −4x2 +2x3 +2x4 = −5,

2x1 −8x2 +2x3 +4x4 = −4, x1 −4x2 +x3 +2x4 = −2.

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 1314 / 1814 15 16 17 18 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
23.11.201983.02 Кб3Сам.работа №2.docx
#
26.03.2016155.91 Кб6санди таймс.docx
#
01.09.201942.55 Кб4Сара Брайтман.docx
#
29.08.2019540.18 Кб4сборник 2.rtf
#
09.11.2019200.19 Кб26Сборник Essay.doc
#
26.03.20161.04 Mб324Сборник задач по высшей математике.pdf
#
10.11.20193.13 Mб10Сборник инд.зад. по электронике.doc
#
13.11.20191.09 Mб28Сборник тестов по СГМУ.doc
#
02.06.2015364.24 Кб26Сборник+задач.Часть+2.pdf
#
02.06.20154.04 Mб48сборник_конституционное_право_и_политика.pdf
#
25.11.2019847.87 Кб25Сборник_практ.doc