Бусыгин

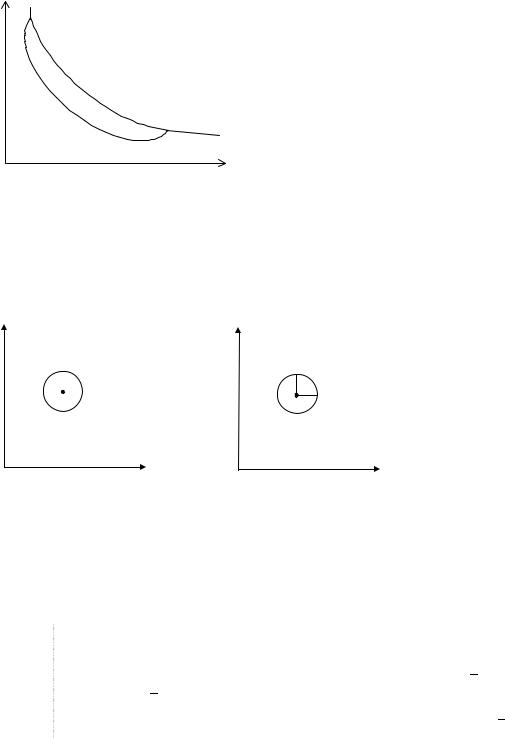
41

•предпочтений с «толстой» кривой безразличия, т.е. ситуации в которой существует окрестность некоторой точки, в которой все наборы одинаково желаемы для потребителя (смотри рисунок 5).

Связь между понятиями строгой монотонности и локальной ненасыщаемости, в принципе, очевидна. Если предпочтение является строго монотонным, то оно локально ненасыщаемо. Обратное, вообще говоря, неверно.

x2

x1

Рисунок 5. «Толстая» кривая безразличия

Рисунок 6 показывает разницу между понятиями строгой монотонности и локальной ненасыщаемости. Заштрихованная область на первой части рисунка показывает ту зону, в которой могут находиться лучшие наборы при выполнении свойства локальной ненасыщаемости. Аналогично, заштрихованная область на второй части рисунка показывает зону, где находятся лучшие наборы для предпочтений, обладающих свойством строгой монотонности.

Рисунок 6 Строгая монотонность и локальная ненасыщаемость

Следующая группа свойств предпочтений, которую мы рассмотрим, важна для демонстрации «хороших» свойств функции выбора/спроса и доказательства существования равновесия.

Здесь и далее мы будем предполагать, что множество X выпукло.

Определение 8.

Предпочтения называются выпуклыми в X, если x,y X: x }y и 0<α<1 выполнено

αx + (1 – α)y }y.

Предпочтения называются строго выпуклыми в X, если x,y X: x }y, x ≠ y и 0 < α < 1 выполнено αx + (1 – α)y } y.

Как не сложно понять определение выпуклости (строгой выпуклости) означает выпуклость верхнего лебеговского множества введенного нами в предыдущем параграфе. Остановимся теперь на различии понятия строгой выпуклости от «просто» выпуклости. Грубо говоря, различие между этими понятиями состоит в том, что при выполнении свойства

41

42

строгой выпуклости запрещена ситуация, когда граница верхнего лебеговского множества (или, что тоже самое, кривая безразличия) имеет «линейные» части. На Рисунке 7 изображен пример выпуклого, но не строго выпуклого отношения предпочтения.

x2

x1

Рисунок 7. Пример выпуклых, но не строго выпуклых предпочтений

С понятием выпуклости предпочтений, в случае их представимости функцией полезности, тесно связаны свойства вогнутости23 и квазивогнутости функции полезности. Оказывается, что для вогнутой функции полезности справедлив следующий результат:

Теорема 10.

Если функция полезности вогнута, то представляемые ею предпочтения выпуклы.

Доказательство:

По определению вогнутости u(.) имеем, что x,y X

u(αx + (1 – α)y) > αu(x) + (1– α)u(y) 0 <α <1,

Без потери общности считаем, что x}y. Тогда в силу определения функции полезности имеем: u(x) > u (y), откуда

u(αx + (1–α)y) > u(y),

или

αx + (1 – α)y}y 0<α<1.

Что и означает выпуклость предпочтений.

*

Обратное, вообще говоря, не всегда верно. Выпуклость предпочтений эквивалентна квазивогнутости функции полезности.

Определение 9.

Функция u : X→Ê называется квазивогнутой, если

u(αx + (1 – α)y) >min(u (x), u(y)) 0<α <1.

Функция u : X→Ê называется строго квазивогнутой, если

23 Напомним, что функция u(.) — вогнута, если u(αx+(1–α)y)> αu(x) +(1– α) u(y) 0<α<1. Классический результат математического анализа говорит, что дважды непрерывно дифференцируемая функция u(.) вогнута тогда и только тогда, когда ее матрица вторых производных (матрица Гессе) H отрицательно полуопределена на внутренности ее области определения, т.е. z′Hz<0 z. (См. например, Рокафеллар, Р., Выпук-

лый Анализ, Москва, Мир, 1973, Гл. 1, §4)

42

43

u(αx + (1 – α)y) > min(u (x), u(y)) 0<α<1.

Отметим также, что дважды непрерывно дифференцируемая функция u : X→Ê квазивогнута тогда и только тогда, когда ее матрица H вторых производных отрицательно полуопределена на u(x)z = 0, где x принадлежит внутренности области определения X. Другими словами, для каждого z, такого что u(x)z = 0 выполнено z′H(x)z<0, где x принадлежит внутренности X24.

Теорема 11.

Функция полезности квазивогнута тогда и только тогда, когда представляемые ею предпочтения выпуклы.

Доказательство:

Доказательство этого факта несложно и оставляется читателю в качестве упражнения.

*

Из двух предыдущих теорем ясно видно, что каждая вогнутая функция является квазивогнутой. Следующий пример показывает, что обратное не верно и класс квазивогнутых функций шире класса вогнутых функций, а заодно и проиллюстрирует технику проверки квазивогнутости.

Пример 4.

Рассмотрим функцию u(x)=x1x2, заданную на неотрицательном ортанте Ê2+ . Покажем, что эта функция квазивогнута, но не является вогнутой.

Способ 1 (По определению)

Возьмем два произвольных вектора x,y Ê2+ . Тогда для любого 0<α <1 имеем

(αx1 + (1 – α)y1)( αx2 + (1 – α)y2) = α2x1x2+(1 – α)2y1y2+α(1 – α)x1y2+α (1 – α)x2y1

Без потери общности будем считать, что y1y 2> x1x2. Если компоненты вектора x не равны

хотя бы одна из компонент вектора x равна 0, очевидна. Таким образом, для любых x,y Ê2+ таких, что y1y 2> x1x2, имеем x1y2+x2y1>2x1x2. С учетом изложенного, получаем

α2x1x2+(1 – α)2y1y2+α(1 – α)x1y2+α (1 – α)x2y1> (α2+(1 – α)2+2α(1 – α)) x1x2 = x1x2=min{x1x2, y1y 2 }

Таким образом, квазивогнутость функции x1x2 доказана.

Покажем теперь, что эта функция не является вогнутой. Возьмем два вектора x=(1, 1), y=(2, 2) и α = 12. Но тогда u(αx +(1 – α)y)= 94 и αu(x)+ (1 – α)u(y)= 52. Поскольку 52 > 94, то функция не является вогнутой.

Способ 2 (С использованием матрицы Гессе)

24 Более подробно о дифференциальных свойствах квазивогнутой функции полезности смотри: Barten, A.P., Bohm, V., Consumer Theory, in Handbook of Mathematical Economics, V.2, K.J. Arrow, M.D. Intriligator, eds., North-Holland, 1982 (pp. 403-09), и содержащиеся там ссылки.

43

44

Несложно проверить, что матрица H вторых частных производных функции u(x)=x1x2 имеет вид

H= 01 01 .

Однако данная матрица не является отрицательно полуопределенной. Действительно, для вектора z′=(1, 1) имеем z′Hz= 2 > 0. Таким образом, функция не является вогнутой. Покажем, что она квазивогнута. Несложно увидеть, что z′Hz=2z1z2. Рассмотрим знак этой квадратичной формы при всех z таких, что u(x)z = 0, т.е. при всех z таких, что x2z1 + x1z2=0. Умножив это равенство на z1, получим x2(z1)2 + x1z1z2=0. На внутренности поло-

жительного ортанта имеем z′Hz=2z1z2= – 2xx2 (z1)2<0. Таким образом, получили квази-

1

вогнутость функции u(x)=x1x2.

Как не сложно заметить, монотонно возрастающее преобразование ln(.) данной квазивогнутой функции переводит ее в вогнутую. Действительно матрица Гессе, для таким образом преобразованной функции, будет равна

Подобная ситуация достаточно типична и прорешав достаточно много типовых задач может сложиться мнение, что каждая квазивогнутая функция переводится монотонно возрастающим преобразованием в вогнутую функцию и, в этом смысле, два эти класса функций эквивалентны. Отметим, однако, что это не так. Например, функция f(x1, x2)=(x1 – 1)

+ (1 – x1)2 + 4(x1 + x2) квазивогнутая. Её линии уровня – непараллельные, прямые линии. Можно показать, что эта функция не может быть трансформирована в вогнутую функцию монотонным возрастающим преобразованием. Следует оговориться, что большинство подобных примеров достаточно причудливы и их построение требует достаточной изобретательности.

Как мы выяснили в предыдущем параграфе, функции переводящиеся друг в друга монотонно возрастающим преобразованием эквивалентны с точки зрения упорядочивания потребительских наборов. В связи с этим, естественно возникает вопрос о том, какие свойства функции полезности, помимо ранжировки потребительских наборов, сохраняются при трансформации функции полезности. Естественно ожидать, в силу того, что мы действуем на функцию полезности монотонно возрастающим преобразованием, сохранения свойств монотонности, строгой монотонности и локальной ненасыщаемости. Вопрос же о сохранении свойств вогнутости и квазивогнутости функции полезности не так очевиден.

Теорема 12.

Пусть f:Ê→Ê – монотонно возрастающая функция, а u:X→Ê – некоторая квазивогнутая функция, заданная на выпуклом множестве X, тогда их суперпозиция также будет квазивогнутой функцией.

Доказательство:

Доказательство этого факта несложно, следует напрямую из определений квазивогнутости и монотонности и оставляется читателю в качестве упражнения.

*

44

45

Стоит отметить, что, вообще говоря, в отличие от свойства квазивогнутости, свойство вогнутости не сохраняется при монотонно возрастающем преобразовании, что показывает следующий пример.

Пример 5.

++ . Подвергнем u(.) монотонно возрастающему преобразованию f(y)= y3 и покажем, что функция u^(x)=f(u(x))= (ln(x))3 не является вогнутой. Найдем вторую производную данной функции

Нетрудно заметить, что вторая производная функции u^(.) может быть как положительной, так и отрицательной и, таким образом, функция u^(.) не является вогнутой. Отметим, что, тем не менее, данная функция является квазивогнутой. (Проверьте это!) Этот результат, вообще говоря, не удивителен, так как выше мы установили два факта: 1) каждая вогнутая функция является квазивогнутой; 2) монотонно возрастающее преобразование переводит квазивогнутую функцию в квазивогнутую.

Рассмотренные выше свойства выпуклости и строгой выпуклости предпочтений тесно связаны с понятием предельной нормы замены25. Покажем теперь, что из выпуклости предпочтений следует закон неубывания предельной нормы замены.

Предположим, что предпочтения потребителя представимы дважды непрерывно дифференцируемой квазивогнутой функцией полезности u: Ên+ →Ê. Содержательно, норма замены указывает на то количество блага j, на которое необходимо сократить потребление этого товара в обмен на увеличение потребления блага i с тем, чтобы уровень полезности потребителя и количество всех остальных товаров оставались неизменными. Таким образом, в случае если количество блага i изменяется на дифференциально малую величину dxi, то для того, чтобы потребитель остался на той же самой кривой безразличия u(x) = u- количество блага j при условии что количество остальных благ остается неизменным должно измениться на величину dxj такую что

ui′(x) dxi + uj′(x) dxj = 0.

Отсюда

25 Возможно, что впервые связь между поведением предельной нормы замены и выпуклостью предпочтений было отмечена Джоном Хиксом и Роем Алленом: «Принцип убывающей предельной полезности должен уступить место возрастающей предельной нормой замены…. Это условие выражается на диаграмме безразличия с помощью кривых безразличия, выгнутых по направлению к осям.» (Hicks, J.R., Allen R.G.D., A Reconsideration of the Theory of Value, Economica, 1934 (Цитировано по: Теория потребительского поведения и спроса, под ред. В.М. Гальперина, Спб.: Экономическая Школа, 1993 )).

45

46

Под предельной нормой замены i-ым благом j-ого обычно понимается величина

MRSij(x) = – ui′′(x) . uj (x)

Найдем производную предельной нормы замены по xi, помня о том, что количества благ, кроме i-го и j-го, не изменяются, и, мы находимся на одной и той же кривой безразличия (т.е. фактически предполагая зависимость xj от xi). В этом случае

Проверим, что закон неубывания предельной нормы замены выполняется, если функция полезности квазивогнута, или, что тоже самое, предпочтения выпуклы. В случае непрерывной дифференцируемости функции полезности квазивогнутость эквивалентна отрицательной полуопределенности матрицы Гессе на гиперплоскости u(x)z = 0. Рассмотрим вектор z равный 0 для всех индексов не равных i, j и zi = – uj′(x), zj = ui′(x). Очевидно, чтоu(x)z = 0. Проведя непосредственные вычисления, получаем что

z′Hz= (ui′(x))2ujj′′(x) – 2uij′′(x)ui′(x)uj′(x) + (uj′(x))2uii′′(x) < 0.

Таким образом, в случае выпуклости предпочтений при uj′(x) > 0 мы имеем выполнение закона неубывания предельной полезности. Отметим, что в некотором смысле верно и

обратное, т.е. выпуклость предпочтений эквивалентна неубыванию нормы предельной замены26.

В приложениях экономической теории очень часто рассматриваются также дополнительные свойства предпочтений, которые налагают более сильные требования на функцию полезности. Так, например, в макроэкономике при рассмотрении поведения агрегированного потребителя часто предполагается выполнение свойства гомотетичности.

26 Доказательство этого факта смотри в Arrow K.J., Enthoven A.C., Quasi-Concave Programming, Econometrica, V. 29(4), 1961

46

47

Определение 10.

Отношение предпочтения называется гомотетичным , если

(1)для каждого положительного t tx X тогда и только тогда, когда x X.

(2)для каждого положительного t соотношение tx ~ ty выполняется тогда и только тогда, когда выполняется соотношение x~y.

Опираясь, на приведенную в прошлом параграфе схему доказательства существования функции полезности представляющей строго монотонные предпочтения легко показать, что для строго монотонных и гомотетичных предпочтений существует положительно однородная функция полезности, представляющая эти предпочтения. Особенностью положительно однородной функции полезности является то, что предельная норма замены для любой пары товаров остается неизменной на луче tx. Это полезное свойство эквивалентно тому, что кривые Энгеля27 являются лучами, выходящими из начала координат. Кроме того, при выполнении этого свойства, свойств локальной ненасыщаемости, непрерывности и выпуклости, система неоклассических предпочтений допускает представление вогнутой функцией полезности28.

В теории отраслевых рынков важную роль играют предпочтения, обладающие свойством квазилинейности.

Определение 11.

Отношение предпочтения называется квазилинейным на X по K-му благу, если

•для каждого положительного t из x X следует x + teK X;

•для каждого положительного t и x,y X из x~y следует x + teK~ y + teK.

Отношения предпочтения, обладающие данным свойством, допускают представление функцией полезности вида u~(x) = u(x–K) + axK. Эта функциональная форма задает такую систему функций спроса, что спрос на первые K–1 благо не зависит от дохода и, тем самым, для этих благ полностью отсутствует эффект дохода. Данное свойство оказывается полезно при обсуждении агрегирования предпочтений и выяснении влияния изменения параметров модели (например, цен и доходов) на благосостояние потребителя.

Наконец в макроэкономике, обычно рассматриваются функции полезности потребителя

n

вида u(x)=Ûui(xi). Такие функции полезности получаются в случае так называемых сепа-

..., K}, Ni]Nj= при i≠j и, кроме того, X =X1 ×X2 ×...× Xs. Такое разбиение допустимого потребительского множества довольно естественно, если мы рассматриваем предпочтения индивидуума во времени, и Xi рассматривается как «сужение» допустимого потребительского множества на i–ый период (год). Отметим, что неявно предполагается такая нумерация благ, где номера благ из Ni+1 идут сразу за номерами благ из Ni. Если исходно это не так, то данного свойства можно достичь простой перенумерацией.

Определение 12.

47

48

Отношение предпочтения называется слабо сепарабельным, если для разбиения {Nj}sj=1 множества {1, ..., K} из того, что (xj,x^–j)} (yj,y^–j), для xj,yj Xj и некоторых x^–j,y^–

jΠi≠jXi следует что (xj,x–j) } (yj,y–j) для всех x–j,y–jΠi≠jXi.

Очевидно, что в случае, если предпочтения представимы аддитивно–сепарабельной функцией полезности, то это свойство выполнено, и, ранжировка потребительских наборов x=(x–I, xI) и x′=(x′–I, xI) не зависит от значений xI. Очевидно, также, что данное свойство должно быть выполнено при любом выборе подмножества I. Данное соображение мотивирует следующее определение:

Определение 13.

Слабо сепарабельные отношения предпочтения называются строго сепарабельными, если свойство слабой сепарабельности выполняется при любом разбиении множества {1,

..., K}.

Относительно предпочтений удовлетворяющих свойству строгой сепарабельности справедливо, что непрерывные предпочтения строго сепарабельны, тогда и только тогда, когда каждое их непрерывное представление функцией полезности аддитивно–сепарабельно29. Данный тип предпочтений позволяет нам гарантировать отсутствие товаров Гиффена и многие другие полезные свойства функции спроса.

Итак, к данному моменту отталкиваясь от нескольких достаточно разумных аксиом о свойствах индивидуальных предпочтений, были получены достаточные условия существования функции полезности и рассмотрены условия на предпочтения, гарантирующие такие ее естественные свойства как монотонность, квазивогнутость и т.д. Тем самым, был описан способ, которым потребитель упорядочивает потребительские наборы из множества допустимых альтернатив. Для того чтобы перейти к анализу выбора потребителя осталось рассмотреть дополнительные ограничения на альтернативы, которые совместно с ограничениями налагаемыми множеством допустимых альтернатив и формируют ту ситуацию выбора, с которой сталкивается потребитель.

Задачи

38.

A) “…suppose we choose x1~ x2. Point x1 represents a bundle containing a proportion of the good x1 which is relatively “extreme,” compared to the proportion of x1 in the other bundle x2. The bundle x2, by contrast, contains a proportion of the other good, x2, which is relatively extreme compared to that contained in x1. Though each contains a relatively high proportion of one good compared to the other, the consumer is indifferent between the two bundles. Now, any convex combination of x1 and x2, such as xt, will be a bundle containing a more “balanced” combination of x1 and x2 than does either “extreme” bundle x1 or x2 ”30

Б) “Условие выпуклости … чрезвычайно важно и более ограничительно. Оно означает, что если каждый из двух векторов x’, x’’ предпочитается третьему вектору x, то любая их “смесь” αx’+(1-α) x’’, 0 < α < 1 также считается лучше x. Вполне вероятно, что вы любите виноградный и томатный соки больше яблочного, но это вовсе не означает, что вы

29Подробнее о сепарабельности предпочтений смотри Barten, A.P., Bohm, V., Consumer Theory, in Handbook of Mathematical Economics, V.2, K.J. Arrow, M.D. Intriligator, eds., North-Holland, 1982 (pp. 392-94), и содер-

жащиеся там ссылки.

30Jehle, G.A. and Reny P.J., Advanced Microeconomic Theory, Addison-Wesley, 1998, p. 118

48

49

предпочтете выпить вместо стакана яблочного стакан смеси из виноградного и томатного соков. Однако в теоретических рассуждениях обычно рассматривают потребление за более длительный промежуток времени, например за год. Тогда выпуклость предпочтений в приведенном выше примере означает, что если вы предпочитаете виноградный и томатный соки яблочному, то вы готовы также пить часть года первый из них, а оставшуюся часть – второй вместо яблочного круглый год. Такое допущение вполне правдоподобно, хотя возможны и возражения. Одно из них состоит в том, что предпочтение зависит от способа чередования напитков в течении года. Другое, быть может, более существенное, относится к самому методу описания поведения: мои предпочтения могут меняться в зависимости от многих причин, например от самочувствия, так что говорить о предпочтении одного потребительского набора другому не имеет смысла.”31

Прокомментируйте эти цитаты. Согласны ли Вы с ними? Если нет, то почему?

39.Покажите, что функция полезности монотонна (не убывает) тогда и только тогда, когда монотонно представляемое ею отношение предпочтения.

40.Покажите, что строго монотонные предпочтения локально ненасыщаемы. Приведите пример монотонных предпочтений, не обладающих свойством локальной ненасыщаемости.

41.Приведите пример выпуклых локально ненасыщаемых предпочтений, которые не обладают свойством монотонности.

42.Покажите, что строго выпуклые монотонные предпочтения локально ненасыщаемы.

43.Покажите, что если полные транзитивные и непрерывные предпочтения заданы на компактном множестве X, то эти предпочтения не могут обладать свойством локальной

ненасыщаемости.

44.Будем говорить, что предпочтения обладают свойством сильной монотонности, если существует, по крайней мере, одно благо, большее количество которого строго предпочитается меньшему. Запишите формально это определение. Как это свойство соотносится со свойствами монотонности и строгой монотонности? Покажите, что из свойства сильной монотонности следует свойство локальной ненасыщаемости.

45.Пусть предпочтения потребителя заданы посредством полного и транзитивного бинарного отношения. Покажите, что предпочтения потребителя выпуклы тогда, и только

тогда, когда выпукло множество нехудших элементов, т.е. множество L+(y)={x X|x } y}.

46. Приведите пример непрерывной квазивогнутой функции полезности, не являющейся монотонной.

31 Полтерович, В.М., Экономическое равновесие и хозяйственный механизм, М.: Наука, 1990, стр. 10.

49

50

47.Покажите, что если функция полезности строго вогнута, то представляемые ею предпочтения строго выпуклы.

48.Покажите, что функция полезности строго квазивогнута тогда и только тогда, когда представляемые ею предпочтения строго выпуклы.

49.Покажите, что если дважды непрерывно дифференцируемая функция полезности строго вогнута, то для этой функции выполняется закон Госсена об убывании предельной полезности. Верно ли утверждение о том, что из закона Госсена не следует выпуклость предпочтений?

50.Докажите теорему 11.

51.Докажите теорему 12.

52.Покажите, что отношение предпочтения, задаваемое положительно однородной (первой степени) функцией полезности обладает свойством гомотетичности.

53.Покажите, что полное, транзитивное, гомотетичное и непрерывное отношение предпочтения представимо однородной функцией полезности.

54.Пусть предпочтения обладают свойствами полноты, транзитивности, непрерывности и гомотетичности и задаются на Ên+. Известно, также, что они представимы аддитивносепарабельной функцией полезности, т.е. в виде

u(x) = Ûui(xi).

Покажите, что

u(x) = Ûaixiρ

единственная (с точностью до монотонно возрастающего преобразования) функция, удовлетворяющая этим требованиям. Каковы ограничения на параметры ai и ρ в случае если предпочтения ко всему прочему обладают свойством строгой монотонности? Докажите, что функция

u′(x) = (Ûαixiρ)1/ρ,

где Ûαi=1, αi>0 порождается теми же предпочтениями, что и u(x) = Û aixiρ.32

55. (Продолжение) Покажите, что функция полезности

32 Рассмотренная в данном упражнении функция имеет специальное название – функция с постоянной эластичностью замены, или, CES-функция (constant elasticity of substitution). Впервые в контексте микроэконо-

мической теории она была рассмотрена в работе: Arrow, K.J., Chenery, H.B., Minhas, B.S., Solow, R.M., Capi- tal–Labor Substitution and Economic Efficiency, Review of Economics and Statistics, V. 43, 1961.

50