
математика_шпоры
.docx|
1.Мера плоской области. Пусть U –плоское мн-во, будем наз его ограниченным, если сущ круг , который охватывает это мн-во. Наименьший диаметр такого круга- диаметр мн-ва α(U).площадь- мера (m). Мн-во U наз измеренным, если выполн равенство m_(U)=m+(U). m(U)=m_(U)=m+(U)-мера. Плоское мн-во огранич векторами – область. Т. Ограниченная плоская обл измерима, т.е. для нее определено понятие площади. Плоскую кривую можно считать замкнутой обл если ее площадь=0.
|
2. Определение и св-во двойного инт-ла. Пусть Д- огранич плоская обл. Р принадлеж Д- переменная точка этой обл.f(p)-числовая фун-ия, опред в обл Д. ∫∫дf(p)dδ. ∫∫дf(p)dδ= lim h->∞S(f,B(черточка вверху).- опред инт-ла без ввода сист корд-ых плоскостей. Предположим, что сист корд введена:Р:Р(х,у),f(p)=f(x,y), dδ = dxdy, получ ∫∫дf(x,y)dxdy. Св-ва :1. ∫∫д1 dδ = δ(Д)2. ∫∫дαf(p)dδ= α∫∫дf(p)dδ 3. ∫∫д(f(p)+g(p)) dδ = ∫∫дf(p)dδ+ ∫∫дg(p)dδ 4. Если f(p)=<g(p) то ∫∫дf(p)dδ=< ∫∫дg(p)dδ 5. область Д замкнута(содержит свою границу )и f(p) непрерывна( достигает миним. обозн m и максим. обзн M) mδ(Д)=< ∫∫дf(p)dδ=<M δ(Д) 6.если обл Д замкнута и непредставима в виде объединения замкнутых обл, то р* принадлеж Д, ∫∫дf(p)dδ=f(p*) dδ(интегральная теорема о среднем) 7. Д=Д1UД2,Д1иД2 пересек только по граничным точкам. ∫∫дf(p)dδ= ∫∫д1f(p)dδ+∫∫д2f(p)dδ |
3.правильность обл вдоль оси. Определение повторного интеграла. Огран обл Д наз првильной вдоль оси l если прямая, проходящая через внутр точки обл Д, паралл оси l, пересек границу обл Д ровно 2 раза(имеет 1 точку входа и 1 выхода).прямую проход через внутр точки обл назовем сквозной. Если обл неправильная то ее можно разрезать на несколько правильных частей. 1 Д правильна вдоль оси Оу. Множество точек входа образует нижнюю границу обл Д , а мн-во точек выхода – верхнюю границу. 2. Д правильна вдоль оси Ох, мн-во точек входа- левая граница обл, мн-во точек выход –правая граница. Рассмотрим обл Д, прав вдоль Оу, пусть у=α1(х)и у= α2(х)-верхняя и нижняя граница при хЄ[a,b],пусть f(x,y)-опр на Д.∫от a до b (∫от α1(х)до α2(х) f(x,y)dy)dx –повторный инт-л. Внутренний вычисляется в первую очередь. Iy (f,Д)= ∫от a до b (∫от α1(х)до α2(х) f(x,y)dy)dx. Iх (f,Д)= ∫от a до b (∫от α1(х)до α2(х) f(x,y)dх)dу. |
4.свойства повторного инт-ла. 1.Iy(1,Д)=δ(Д) 2.Iy(αf,Д)=αIy(f,Д) 3.Iy(f+g,Д)=Iy(f,Д)+Iy(g,Д) 4.если f(x,y)=<g(x,y)то Iy(f,Д)=<Iy(g,Д) 5.если обл Д замкнута, а f(x,y)непрерывна, m =min f(x,y),а M=max f(x,y), т o m*δД=<Iy(f,Д)=<Mδ(Д).6.если обл Д замкнута, а f непрерывна, при чем Д не состоит из разл замен частей , то сущ точка С(α,β), что Iy(f,Д)=f(α,β)δД.7.обл Д прав по Оу , сквозная прямая разбивает (паралл Оу)обл Д на альфа обл-ти (правильные), а сквозная прямая паралл Ох на большее число правильных обл.8.пусть Д является прямоугольником огранич прямыми х=а,х=в,у=с,у=d,f(x,y)=<f1(x)f2(y). Iy(f,Д)=∫от а до в f1(x)dx*∫от c до d f2(y)dy, Ix(f,d)=∫от а до в f1(x)dx*∫от c до d f2(y)dy, Ix= Iy=∫от а до в*∫от c до d.
|
5. Равенство двойного и повторного интеграла. Пусть Д – правильная вдоль ОУ плоская область. Пусть f(x;y) определенная на ней непрерывная ф-ция. Правильность области позволяет записать Iy(f;Д) и справ-во рав-во: =Iy(f;Д) (1). =Iх(f;Д) – если обл прав вдоль ОХ. Д-во – разбиение обл Д сеткой горизонт и вертикальн прямых.
|
|
6. Замена переменных в двойном интеграле. Линейная замена. Рассм
на корд плоскости Оху обл Дху и
опредеенную на ней ф-цию f(x;у).
Пусть в пространстве Ouv
дана обл Дuv.
Пусть определено взаимообратное
выражение ɸ : Дuv
→ Дху, |
7. Переход к полярным координатам в двойном интеграле. Рассм
коорд плоскость Оху. Точку М(х;у) можно
охарактеризовать 2-мя параметрами
ρ=ОМ, φ=угол между ОМ и Ох. Пара(ρ;φ) –
полярные координаты т.М. Очевидно, что
ρ>=0, φ можно считать изменяющимся в
пределе любого промежутка от 0 до 2П.
|
8. Геометрические приложения 2-го интеграла: площадь плоской фигуры, объем цилиндроида, площадь поверхности. 1)Площадь
плоской фигуры. Нам известна ф-ла
Ϭ(Д)=
|
9. Определение числового ряда, его сходимости и расходимости. Необходимое условие сходимости. Бесконечная
сумма а1+а2+…+аn+…(1)
назыв-ся числовым рядом. Частичная
сумма - Sn=
а1+а2+…+аn.
Если
последовательность (Sn)
явл-ся схдящейся, т.е. имеет предел
|
10. Признак сравнения (элементарная и предельная форма). Элементарн
пр-к сравн-я:
Пусть
а1+а2+…+аn+…
- ряд с положит членами, b1+b2+…+bn+…
an
≤
bn.
Тогда сход-ть 2-го ряда влечет сход-ть
1-го. Расход-ть 1-го след-т расход-ть
2-го. Предельн пр-к сравн-я: а1+а2+…+аn+…,
b1+b2+…+bn+….
аn,
bn
≥0.
1)A≠0, ∞. Ряды вместе сход-ся и расх-ся. Если А=0, то 1-й расх-ся => 2-й расх-ся. А=∞, то 1 сх => 2-й сх (2 расх => 1 расх). А= +∞ 2 расх => 1 расх. bn=qn-1, если q<1 – сход-ся, q≥1 – расх. bn =1/np. р>1 сход, р≤1 расх.
|
|
11. Признак Даламбера и радикальный пр-к Коши. Пр-к
Даламбера: пусть а1+а2+…+аn+…
ряд с положит членами.
|
12. Интегральный пр-к Коши. Рассм
ряд с положит членами а1+а2+…+аn+…,
удовл услов-м: 1) an+1≤
an,
2)an→0,
т.е.
|
13. Знакоперемееный ряд. Абсолютная и условная сходимость. Знакопеременный ряд – ряд а1+а2+…+аn+…(1), члены которого приним-т значения обоих знаков. Причем это происх-т при сколь угодно больших знач-х n. Ряд (1) позвол-т построить 2-1 ряд bn= | аn |: b1+b2+…+bn+….(2). Ряд (2) – ряд с положит членами. Сходимость ряда (1) при сход-ти ряда (2) назыв-ся абсолютной сход-тью. Сход-ть ряда (1) при расход-ти ряда (2) назыв-ся условной сход-тью.
|
14. Ряд Лейбница. Вычисление суммы ряда Лейбница с заданной точностью. Ряд
Лейбница удовлетворяет след условиям:
1) знакочередующийся; 2) an
стремится к 0; 3) |an|
убывает и стремится к 0 – такой ряд
сходится; 4) |Sn|<|a1|;
5) |Rn S=Sn+Rn
- для любого сходящегося ряда. S
приблизительно = Sn
при этом |Rn |
15. Степенной ряд. Т. Абеля. Радиус и интервал сходимости. Стр-ра области сходимости. Степенной ряд – функцион-й ряд (бескон сумма, слагаемые кот явл-ся ф-циями) с общим членом un(х)=cnxn, где cn - конст-та. Нумерация членов ряда начин-ся с n=0. T.O. мы получаем ряд вида: c0+ с1х+с2х2+ …+ сnxn + …(1) Т. Абеля. Если ряд (1) сходится при х=х0, х0≠0, то он абсолютно сходится при любых значениях х, удовлетворяет нерав-ву |х|˂|х0|, хϵ(-|х0|;|х0|). Пусть
сущ-т
|
|
16. Определение и сходимость ряда Маклорена. Если
х0=0,
то ряд Тейлора назыв-ся рядом Маклорена,
и ф-ла Маклорена примет вид:
f(h)=f(x0)+(1/1!)f'(0)h+…+(1/n!)f(n)(0)hn.
Вместо буквы h
можно вставить х. Для получения общего
вида ф-лы Маклорена можно исследовать
остаточн член
|
17. Ряды Маклорена функций ех, sin x, cos x. Возьмем
ф-цию f(x)=
ех.
Она имеет бесконечное число производных
f’(x)=
ех,
f’’(x)=
ех,
…., fn(x)=
ех.
f(0)=
1, f’(0)=1,
f’’(0)=1,
…, f(n)
(0)=1. f(x)=1+(1/1!)x+(1/2!)x2+..+(1/n!)xn+Qn(x).
f(x)=sin
x,
f’(x)=cos
x,
f’’(x)=
- sinx,
f’’’(x)=
- cosx,
f4(x)=
sinx.
f(0)=0,
f’(0)=1,
f’’(0)=0,
f’’’(0)=
-1, f4(0)=0.
Sinx=(1/1!)x
|
18.Частота события, её св-ва.Алгебра событий, элементарное событие Частота событий и ее свойства Относительной частотой события А () называется отношение числа m опытов в которых событие А наступило к общему числу n — фактически проведенных опытов. Условной частотой события В по отношению в событию А () называется отношение числа k опытов, в которых наступило событие А и В к опытам m в которых наступило событие А. Алгебра событий. Определение 1.1. Суммой А+В двух событий А и В называют событие, состоящее в том, что произошло хотя бы одно из событий А и В. Суммой нескольких событий, соответ-ственно, называется событие, заключающееся в том, что произошло хотя бы одно из этих событий. Определение 1.2. Произведением АВ событий А и В называется событие, состоящее в том, что произошло и событие А, и событие В. Аналогично произведением нескольких событий называется событие, заключающееся в том, что произошли все эти события. Определение 1.3. Разностью А\B событий А и В называется событие, состоящее в том, что А произошло, а В – нет. Определение 1.4. События А и В называются совместными, если они могут произойти оба в результате одного опыта. В противном случае (то есть если они не могут произойти одновременно) события называются несовместными. Определение 1.5. Говорят, что события А1, А2,…,Ап образуют полную группу, если в результате опыта обязательно произойдет хотя бы одно из событий этой группы. Замечание. В частности, если события, образующие полную группу, попарно несовмест-ны, то в результате опыта произойдет одно и только одно из них. Такие события называют элементарными событиями. Определение 1.6. События называются равновозможными, если нет оснований считать, что одно из них является более возможным, чем другое. |
19.Определение вер-ого пр-ва. Аксиома вер-сти. Пусть A и B — два несовместных события, причем в n испытаниях событие A произошло m1 раз, а событие В произошло m2 раз. Тогда частоты событий A и В соответственно равны P*(A)=m1/n, P*(B)=m2/n. Так как события A и В несовместны, то событие A+B в данной серии опытов произошло m1+m2 раз. Следовательно,
Аксиома
3 допускает обобщение на случай
нескольких событий, а именно: если
события A1, A2, ..., An, попарно несовместны,
то
Событием, противоположным событию A, называется событие Ā, состоящее в ненаступлении события A . Очевидно, события A и Ā несовместны. Теорема 1. Для любого события A вероятность противоположного события Ā выражается равенством P(Ā)=1-P(A) Теорема 2. Вероятность невозможного события равна нулю. |
20.Сов-сть и несов-сть событий. Формулы сложения ве-стей. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления: P(A+B)=P(A)+P(B)-P(AB) Если события А и В являются несовместными(А*В=Ø) то Р(А+В)=Р(А)+Р(В)
|
|
21.Формула уможения вер-стей. Теорема: Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое событие имело место: .P(AB)=P(A)P(B/A)=P(B)P(A/B) 22.Формула полной вер-сти. Формула Байеса. . Полученная формула называется формулой полной вероятности. На основании теоремы о вероятности произведения двух событий: .P(AB)=P(A)P(B/A)=P(B)P(A/B), откуда:
Или
Полученная формула носит название формулы Байеса.
|
23.Схема Бернули и формула Бернули. Рассмотрим послед-сть сост из конечного числа единообразных независимых испытаний(опытов)в каждом из которых с одой и той же вероятностью может появляться интересующее нас событие А. А-успех. N-число опытов.Р(А)=Р – вероятность одного успеха .Вся послед-сть опытов – эксперимет. Эксперимент описывается 2мя параметрами n и Р. Описанный эксперимент порождает вероятностное пр-во которое наз схемой Бернули. Р(μn=k)=Cnkpkqn-k-формула Бернули, где n- число независимых опытов, Р- вероятность успеха в одном опыте. μn=это кол-во успехов, которые произошли в результате экеримента.к- некоторое целое число. 24.Предельная теорема Пуассона в схеме Бернули. Пусть
n
стремится к бесконечности, Р меняется
в месте с n,
что nP
стемится Limn->∞Cnkpkqn-k
= |
25. Предельные теоремы Муавра-Лапласа в схеме Бернулли. Применяем
когда Р не является малым 1).локальная
Limn->∞Cnkpkqn-k
= 2.интегральная
|
26. СВ, закон распределения, ф-ция распределения и её св-ва. Случайной величиной называется переменная величина, которая в зависимости от исхода испытания случайно принимает одно значение из множества возможных значений. Случайные величины делятся на дискретные и непрерывные. 1) Величина называется дискретной, если она может принимать определенные, фиксированные значения.P(ξ=x1)+…+P(ξ=xn)=1 2) Случайная величина называется непрерывной, если она может принимать значения, сколь угодно мало отличающиеся друг от друга. P(ξ=x)=0 Закон распределения случ вел-ны –это перечень всех возможных пром-ов В и вероятностей. Фун-ия распределения СВ ξ наз функция Fξ(x) опред равенство F(x)=P(ξ<x), F(x)=P(ξЄ(-∞,x)) Св-ва:F(-∞)=0///F(+∞)=1///F(x) возраст///F(x)непрерывна слева.P(ξЄ[x1,x2])=F(x2)-F(x1)
|
27.дискретная СВ, ряд распределения, свойства функции распределения ДСВ
определяется тем условием, что
существуют числа х1...хn (до бесконечности),
для которых f(ξ=xi)>0
и p(ξ=xi)+...+p(ξ=xn)=1.
множество, состоящее из изолированных
точек - дискретное. СВ называется
дискретной, если множество ее значений
дискретное. Закон распределения ДСВ
удобно описывать таблицей, в которой
оказываются возможные значения СВ и
вероятности этих возможных значений.
(p(ξ=xi)=pi).
Ряд распределения СВ:
Свойства функции распределения (Fξ(x)=p(ξ<x)): 1).F(-∞)=0. 2).F(+∞)=1. 3).F(x) возрастает. 4).F(x) непрерывна слева.
|
|
28.непрерывная СВ, плотность вероятности. Свойства функции распределения и плотности НСВ
- СВ, для которой при любом х выполняется
равенство p(ξ=x)=0.
Имеет смысл говорить о попадании СВ
в промежуток. СВ называется непрерывной,
если ее функция распределения
непрерывна. СВ называется абсолютно
непрерывной, если ее функция распределения
представлена в виде Свойства
плотности вероятности: 1).f(t)>=0.
2). |
29.функция
случайной величины вида
Предполагается,
что f и F известны. Если α>0.,
Если
α<0.
общая
формула:
|
30.функция
случайной величины вида
Fη(y)=p(η<y)=p(ξ2<y). y<=0, (ξ2<y) невозможно, Fη(y)=0.
y>0,
ξ2<y
<=>
p(ξ2<y)=p(
fη(y)=Fη'(y) y<0, fη(y)=0
y>0,
|
31.математическое ожидание и дисперсия дискретной СВ: определение, вычисление и свойства Математическое
ожидание - среднее значение СВ; числовая
характеристика, вычисляемая по формуле
Свойства М: 1.ξ=С=const, М(ξ)=С 2.η=αξ, М(η)=αМ(ξ) 3.z=ξ+η, M(z)=M(ξ)+M(η) 4.z=ξη, Для независимых СВ: M(z)=M(ξ)M(η)=M(ξη)Дисперсия характеризует разброс значений СВ относительно его среднего значения. D(ξ)=M((ξ-M(ξ))2) Свойства дисперсии: 1.ξ=С=const, D(ξ)=0 2.D(αξ)=α2D(ξ) 3.D(ξ)=M(ξ2)-M2(ξ) - более удобная вычислительная формула. 4.D(ξ+η)=D(ξ)+D(η)+2(M(ξη)-M(ξ)M(η)), Если СВ ξ и η независимы, то D(ξ+η)= D(ξ)+D(η) |
32.математическое ожидание и дисперсия непрерывной СВ: определение, вычисление и свойства
Математическое
ожидание:
1.ξ=С=const, М(ξ)=С 2.η=αξ, М(η)=αМ(ξ) 3.z=ξ+η, M(z)=M(ξ)+M(η) 4.z=ξη Для независимых СВ: M(z)=M(ξ)M(η)=M(ξη) Свойства дисперсии: 1.ξ=С=const D(ξ)=0 2.D(αξ)=α2D(ξ) 3.D(ξ)=M(ξ2)-M2(ξ) - более удобная вычислительная формула. 4.D(ξ+η)=D(ξ)+D(η)+2(M(ξη)-M(ξ)M(η)) Если СВ ξ и η независимы, то D(ξ+η)= D(ξ)+D(η) |

 =
= =
=

 (1). Она была получена как одно из св-в
2-го интеграла. Если область явл-ся
правильной вдоль Оу, то получим ф-лу:
Ϭ(Д)=
(1). Она была получена как одно из св-в
2-го интеграла. Если область явл-ся
правильной вдоль Оу, то получим ф-лу:
Ϭ(Д)= 2) Объем цилиндроида. V(Ω)=
2) Объем цилиндроида. V(Ω)= 3)Площадь
поверхности.
3)Площадь
поверхности.

 (2),
то ряд (1) явл-ся сходящимся. Число S
– его сумма. Если предел (2) не сущ-т,
то ряд расходится и суммы не имеет.
Если lim
Sn
=∞, то ряд имеет бесконечную сумму.
Если ряд сходится, то сумма
(2),
то ряд (1) явл-ся сходящимся. Число S
– его сумма. Если предел (2) не сущ-т,
то ряд расходится и суммы не имеет.
Если lim
Sn
=∞, то ряд имеет бесконечную сумму.
Если ряд сходится, то сумма
 . Необходимое условие сходимости.
Условие
. Необходимое условие сходимости.
Условие  .
Ряд и интеграл либо сх, либо расх
вместе.
.
Ряд и интеграл либо сх, либо расх
вместе. ,
тогда этот предел дает значение радиусв
сходимости: R=
,
тогда этот предел дает значение радиусв
сходимости: R= (2).
Если предположить, что существует
lim
(2).
Если предположить, что существует
lim
 .При исследовании ряда на сход-ть на
концах интервала полезно использовать
след законом-ть, пусть un
.При исследовании ряда на сход-ть на
концах интервала полезно использовать
след законом-ть, пусть un .
C
лежит м-ду 0 и х. Тогда общ вид ф-лы
Маклорена: f(x)
= f(0)+(1/1!)f’(0)x+…+(1/n!)f(n)(0)xn+Qn
(x).
Если Qn
(x)
→ 0 при любом х, то ряд сходится при
любом х, его интервал сходимости (-∞;
+∞).
.
C
лежит м-ду 0 и х. Тогда общ вид ф-лы
Маклорена: f(x)
= f(0)+(1/1!)f’(0)x+…+(1/n!)f(n)(0)xn+Qn
(x).
Если Qn
(x)
→ 0 при любом х, то ряд сходится при
любом х, его интервал сходимости (-∞;
+∞).
 .
Зафиксируем значение х, тогда с=конст-та.
Пусть n→∞.
.
Зафиксируем значение х, тогда с=конст-та.
Пусть n→∞.
 (факториал сильнее показательной).
Это имеет место при любом х (получили
разложение ех
в ряд Маклорена). Исследовать ряд,
стоящий в правой части, на сход-ть нет
необходимости. Qn
(x)
→ 0 при любом х, то ряд сходится при
любом х, его интервал сходимости (-∞;
+∞). f(x)=cosx,
f’(x)=
-sinx,
f’’(x)=
-cosx,
f’’’(x)=sin(x),
fIV(x)
= cosx.
f(0)=1,
f’(0)=1,
f’’(0)=0,
f’’’(0)=
-1, fIV
(0)=1. Запишем ф-лу Маклорена:
cosx=1-(1/2!)x2+(1/4!)x4-(1/6!)x6+..+((-1)m/2m!)
(факториал сильнее показательной).
Это имеет место при любом х (получили
разложение ех
в ряд Маклорена). Исследовать ряд,
стоящий в правой части, на сход-ть нет
необходимости. Qn
(x)
→ 0 при любом х, то ряд сходится при
любом х, его интервал сходимости (-∞;
+∞). f(x)=cosx,
f’(x)=
-sinx,
f’’(x)=
-cosx,
f’’’(x)=sin(x),
fIV(x)
= cosx.
f(0)=1,
f’(0)=1,
f’’(0)=0,
f’’’(0)=
-1, fIV
(0)=1. Запишем ф-лу Маклорена:
cosx=1-(1/2!)x2+(1/4!)x4-(1/6!)x6+..+((-1)m/2m!) . f(2m+2)(x)=(-1)m+1cos
x.
. f(2m+2)(x)=(-1)m+1cos
x.

 .
Пусть
n →∞, n =2m+1 => m→∞. cos
x=1-(1/2!)x2+(1/4!)x4+…+
.
Пусть
n →∞, n =2m+1 => m→∞. cos
x=1-(1/2!)x2+(1/4!)x4+…+ -(1/3!)x3+(1/5!)x5+…+
-(1/3!)x3+(1/5!)x5+…+ -(1/3!)x3+(1/5!)x5+…+
-(1/3!)x3+(1/5!)x5+…+ Таким
образом, частота события A+B
равна сумме частот событий A
и В.
Но при больших n
частоты P*(A),
P*(B)
и P*(A+B)
мало отличаются от соответствующих
вероятностей P(A),
P(B)
и P(A+B).
Поэтому естественно принять, что если
A
и В
— несовместные события, то
P(A+B)=P(A)+P(B)
Изложенное
позволяет высказать следующие свойства
вероятностей, которые мы принимаем в
качестве аксиом.
Аксиома
1.
Каждому
случайному событию A соответствует
определенное число Р(А), называемое
его вероятностью и удовлетворяющее
условию
Таким
образом, частота события A+B
равна сумме частот событий A
и В.
Но при больших n
частоты P*(A),
P*(B)
и P*(A+B)
мало отличаются от соответствующих
вероятностей P(A),
P(B)
и P(A+B).
Поэтому естественно принять, что если
A
и В
— несовместные события, то
P(A+B)=P(A)+P(B)
Изложенное
позволяет высказать следующие свойства
вероятностей, которые мы принимаем в
качестве аксиом.
Аксиома
1.
Каждому
случайному событию A соответствует
определенное число Р(А), называемое
его вероятностью и удовлетворяющее
условию .
Аксиома
2.
Вероятность
достоверного события равна единице.
Аксиома
3
(аксиома сложения вероятностей). Пусть
A и В — несовместные события. Тогда
вероятность того, что произойдет хотя
бы одно из этих двух событий, равна
сумме их вероятностей: P(A+B)=P(A)+P(B)
.
Аксиома
2.
Вероятность
достоверного события равна единице.
Аксиома
3
(аксиома сложения вероятностей). Пусть
A и В — несовместные события. Тогда
вероятность того, что произойдет хотя
бы одно из этих двух событий, равна
сумме их вероятностей: P(A+B)=P(A)+P(B)


 (P->0).
(P->0). при
больших n
и малых Р получаем приближенную формулу
Р(μn=k)≈
при
больших n
и малых Р получаем приближенную формулу
Р(μn=k)≈


 *1/
*1/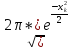 ,xn=(k-nP)/
,xn=(k-nP)/ ,
Р(μn=k)≈
,
Р(μn=k)≈
 *1/
*1/ ,
fi(xk)=
1/
,
fi(xk)=
1/ ,
Р(μn=k)≈
)≈
,
Р(μn=k)≈
)≈
 *fi(xk)
*fi(xk) ,
, (x)dx,
(x)dx,


 ,
f(t) - плотность вероятности.
,
f(t) - плотность вероятности.
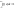 .
.
 .
свойства функции распределения:
1).F(-∞)=0.
2).F(+∞)=1.
3).F(x)
возрастает. 4).F(x) непрерывна.
.
свойства функции распределения:
1).F(-∞)=0.
2).F(+∞)=1.
3).F(x)
возрастает. 4).F(x) непрерывна. ,
формулы для
,
формулы для
 и
и

 ,
,
 .
.
 ,
,
 ,
,

 ,
формулы для
,
формулы для
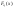 и
и

 ,
,
 )=Fξ(√y)-Fξ(-√y)=Fη(y).
)=Fξ(√y)-Fξ(-√y)=Fη(y).
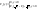

 .
Если множество значений бесконечно,
то в правой части стоит бесконечная
сумма, т.е. ряд расходится, СВ
математического ожидания не имеет.
.
Если множество значений бесконечно,
то в правой части стоит бесконечная
сумма, т.е. ряд расходится, СВ
математического ожидания не имеет. ,
где fξ(x)
- плотность вероятности ξ. Если интеграл
расходится, то СВ математического
ожидания не имеет.Дисперсия:
D(ξ)=M((ξ-M(ξ))2),
D(ξ)=M(ξ2)-M2(ξ),
для второй формулы:
,
где fξ(x)
- плотность вероятности ξ. Если интеграл
расходится, то СВ математического
ожидания не имеет.Дисперсия:
D(ξ)=M((ξ-M(ξ))2),
D(ξ)=M(ξ2)-M2(ξ),
для второй формулы:
 .Свойства
М:
.Свойства
М: