
Шпоры высш. матем
..docx|
1.Функция двух переменных. Определение. Геометрическое изображение.
Опр.
Пусть Д некоторое множество (·) М (x,
y),
є плоскости. Правило f
ставящие в соответствие (·) (x,
y),
определённое единственное число z
у множество действительных наз.
функцией
двух переменных
z=f(x,
y)
– функция двух переменных, где (x,
y)
– независимая переменная, z
– функция. Множество Д – наз. Областью
определения функции множество є
состоящая из чисел {z
є |B, для которых z=f(x,
y)}
наз. областью значений. Пр.
Правило f:
(x,
y)―>
(x²-y²)
ставящие
в соответствие каждая пара (x²-y²)
определяет
функцию двух переменных z=x²-y².
Пр.
Найти область определение функции
двух переменных и изобразить на
плоскость z
= 1/√1-x²-y²
Д (z):
пару чисел {(x,
y):1-x²-y²>0}
1- x²-y²>0;
1> x²+y²
построим границу области 1= x²+y²
- окружность цент О, радиус 1. (·)(0,0)→
1,0²+0² - верно. Область определения явл.
(·)лежащей в нутрии границы. Граница не входит в область определения. Аналогично определяется количество двух и более переменных. Двух переменных функцию можно изобразить графически. Для этого в (x, y) є Д вычисляется значение z=f(x, y). Тройка чисел (x, y,z) определяет в системе координат О x,y,z некоторую точку Р совокупность точек представляет собой некоторую поверхность которая и явл. графиком функции z=f(x, y). Предел функции в точке. Для функции двух переменных вводиться понятие предела функции, непрерывность аналогично случаю функции одной переменной. Введём понятие окрестность точек. Опр. Множество всех (·)М (x, y), плоскости координаты которых удовлетворяет неравенству √(x-x0)²+(y-y0)²<δ (дельта) наз. дельта окрестностью точки М0 (x0, y0). Другими словами δ окрестности (·) М0 (x0, y0) это внутренние (·) круга с центром М0 и радиусам δ. Опр. Пусть функция z=f(x, y) определена в некоторой окрестности (·) М0 с координатами (x0, y0) кроме самой (·) М0. Числа А – наз. пределом функции z=f(x,y), в(·) М0 то есть при х→ x0, y→ y0 Если для любого множества ε сущ. δ>0, что для всех (·) х, не х≠x0, y≠y0 → неравенство | f(x, y)-А|<ε lim f(x, y)=A(х→x0, y→y0 Геометрический смысл: каково бы ни было число ε надеться δ окрестность в (·)М0, что во всех (·)≠0, аппликаты соответствующих (·)поверхности z=f(x, y), отличаются от числа А, по модулю< чем ε (ипсилон). Если предел сущ. то он не зависит от пути по которому (·)М→ М0. Пр. Найти предел функции. lim x→0 y→0x²-y²/x²+y²=0/0 Пусть (·) М(x, y) приближается к (·)О (0,0) по прямой y=kx lim x→0 y→0x²-y²/x²+y²= lim x→0 y→0 x²-kx²/ x²+kx²= lim x→0 y→0 x²(1-k²)/ x²(1-k²)=1-k²/1+k². Вывод: функция z=x²-y²/x²+y² в (·) О (0,0) придела не имеет, так как при различных значении k разные. Пр. lim x→0 y→0x²+y²/(√x²+y²+1)-1=[0/0]== lim x→0 y→0 (x²+y²)((√x²+y²+1)+1)/((√x²+y²+1)-1) ²)/ ((√x²+y²+1)+1) = lim x→0 y→0 (x²+y²)((√x²+y²+1)+1)/x²+y²+1-1= lim x→0 y→0 (√x²+y²+1)+1)=2 Предел функции двух переменных обладает свойствами аналогичными свойства предела функции одной переменной, то есть: 1. lim (f+g) = lim f+ lim g; 2. lim f*g = lim f*lim g 3. lim f/g = lim f/lim g, lim g≠0
2.Частные производные первого порядка функции двух переменных. Геометрический смысл.
Пусть
задана функция z=f(x,
y),
дадим независимой переменной х.
приращение Δx,
сохраняя значение у неизменным, тогда
z,
получим приращение, которое наз.
частным
приращением z
по x.
Обозначим Δxz;
Δxz=(x+Δx,
y)-f(x,y).
Аналогично приращение по у: Δуz;
Δуz=(x+нx,
y)-f(x,y).
Полное приращение Δz=f(x+Δx,y+Δy)-f(x,y).
Если сущ. предел lim
Δx→0
Δуz/Δx=
lim
Δx→0
f(x+Δx,y)-f(x,y),
то он наз. частной
производной функции z=f(x,
y),
по переменной х. Обозначается zx',
ðz/ðx,
fx'(x,
y).
Аналогично определяется частное по
у (производная). Обозначается
zу',
ðz/ðу…Частные
производные функции z
находятся как производные функции
одной переменной при условии, что
другая переменная остается константой.
Частные производные находятся по
формулам и правилам для функции одной
переменной. Геометрический смысл
частных производных функции двух
переменных. Графиком функции z=f(x,y)
явл. некоторая поверхность. Графиком
функции z=f(x,y0)
– есть линия пересечения этой
поверхностью с плоскостью, которая
|| плоскости ох z.
Исходя из геометрического смысла
производны для функции одной переменной
fx'(x0,
y0)=tg
L,
где L
угол между осью ox
и касательной проведённой у кривой
z=f(x,y0)
в (x0,
y0,
z0)M0.
Аналогично fy'(x0, y0)=tg β. Пр. Найти частное производное. z=3y-ex²-y+1; z'x(y=const)=0- ex²-y(x²-y)'x+0=- ex²-y*2x; z'y(x=const)=3- ex²-y(x²-y)'y+0=3- ex²-y*(-1)= 3+ ex²-y; Пр. z=ln(x²-y³); z'x(y=const)=(1/ x²-y³)*2x; z'y(x=const)= )=(1/ x²-y³)*(-3y²).
3.Частные
производные высших порядков функции
двух переменных. Частные производные zx', zy' – первого порядка. Частные производные второго порядка ð/ðx (ðz/ðx)=ð²z/ðx²=z''xx ð/ðy (ðz/ðy)=ð²z/ðy²=z''yy ð/ðx (ðz/ðx)=ð²z/ðxðy=z''xy ð/ðx (ðz/ðy)=ð²z/ðyðx=z''yx z''xy, z''yx – наз. смешанные. Аналогично определяются производные частные более высоких порядков. Пр. ð/ðy(ð²z/ðx²) = z''xxy. Если частные производные непрерывны то смеси произв. отличающиеся порядка дифференциалы равны между собой. Пр. Найти частное производное 2 порядка. z=exy² (xy²)x' =y²*x' = y²*1; z x' =exy² *y²; z xx'' = (exy² *y²)x'= y²* exy²*y²= y4* exy²; z y' =exy² *x2y; z yy'' = (exy² *x2y)y'= (exy²)y'*2xy+ exy²*(2xy)y'= = exy²*2xy*2xy+ exy²*2x = 2xexy² (2xy²+1); z'xy = exy²*2xy³+ exy²*2y; z'xy = exy²*2xy³+ exy²*2y; Полный дифференциал – функция двух переменных. Полным приращением функции двух переменных называется величина Δf=f(x+Δx, y+Δy)-f(x,y) (1) Главная часть немного приращение линейно зависящая от величины Δx, Δy, называется полным дифференциалом. df=ðf/ðx*dx+ðf/ðy*dy (2) Полный дифференциал используется для приближенных вычислений, так как Δf≈df (3) Пр. (1.02)3,01 f(x,e)=xy; x0=1, y0=3; f(x0,y0)= 13=1 f( x,y)≈ f(x0,y0)+ ðf(x0,y0)/ðx*x-x0+ðf(x0,y0)/ðy*y-y dx=1,02-1=0,02; dy=3,01-3=0,01; ðf/ðx=yxy-1|x=x0, y=y0;=3*13-1=3; ðf/ðx=xylim x|x=1, y=3;=0; f(1,02; 3,01)≈1+3*0,02=0,06
|
4.Экстремум функции двух переменных. (·)M (x0,y0) – наз. (·) локального максимума функции f (x,y), если выполняется неравенство. f(x,y)≤f (x0,y0) (множества (х, у).єИδ(x0,y0) )(1). (·)M (x0,y0) – наз. (·) локального минимума функции f (x,y), если выполняется неравенство. f(x,y)≥f (x0,y0) (множества (х, у).єИδ(x0,y0) )(2). Максимум и минимум её функции наз. её экстремумом. (·)M (x0,y0) в которой достигается экстремум функции наз. (·) экстремума функции. Теорема 1. (необходимое условие локального экстремума). Если (·)M (x0,y0) явл. (·)локального экстремума, то в этой (·)частной производной часто =0. ð f(x0,y0)/ðx = ð f(x0,y0)/ðy=0; или ходьбы одно из частных не сущ. (·) в которых частный производные = 0, наз. стационарными точками двух переменных функций. То есть если экстремум в (·) М достигается, то она обязательно будет стационарной, однако если (·) М явл. стационарной, то в этой точке не обезательно достигается экстремум. Поэтому должны быть достаточно сформулированы условия сущ. экстремума. А=fxx''; B=fxy''; C=fyy''; Δ=AC-B². Теорема 2 (достаточный условия экстремума локального). Пусть функция f(x,y) имеет непрерывные частные производные, до 3 порядка включительно в некоторый области содержащие стационарную точку М, тогда если: 1) Δ>0, то (·) М (x0,y0) явл. (·) экстремума для данной функции, причем А<0, (·)максимума и А>0 (·)минимума. 2) Δ<0, то (·) М (x0,y0) экстремума нет. 3) Δ=0, то экстремум может быть, а может и не быть, требуются дополнительные исследования. Пр. Найти экстремум двух переменных. z=x²+xy+y²-3x-6y 1) ðz/ðx=2x+y-3=0; y=-2x+3; y=-2x+3; x=0; dz/dy=x+2y-6=0; x+2*(-2x+3)-6=0; -3x=0; y=3; (·) M 2) ð²z/ðz²=2; A=2; ð²z/ðxðy=1; B=1; ð²z/ðy²=2; C=2; |AC-B²|=|AB; BC|=2*2-1²=3. Если Δ>0, то в (·) М, есть экстремум. Т.к. А=2>0, то в (·) М1 – минимум. 3) z min (M1)=0²+0*3+3²-3*0-6*3=-9;
5.Наименьшее и наибольшее значения функции двух переменных в замкнутой области. Пусть z= f(x, y) определены в замкнутой области Д с границей Г, дифференцируема во всех внутренних точках, тогда сущ. точки Р1 (x1, x1) (·)P2(x2, x2) в которых функция z прим. наибольшее и наименьшее значение (глобальный экстремум). (·) Р1 и Р2 или среди стационарных точек в нутрии области Д или среди точек принадлежащие границе. Сравнивая значения функции z в этих точках, и выбираем самое большое (наибольшее) и самое маленькое (наименьшее). Пр. найти наибольшее и наименьшее значение f. Z=3x+y-xy, в области Д: y=x; y=4;x=0. 1.Начертить область Д. 2.Находим стационарные точки. ðz/ðx=3-y=0; y=3; ðz/ðy=1-x=0; x=1; Найдём границы области ОА: x=0→ОА/z=y; z'=1≠0. Исследуем граничные точки.
Границе
АВ: y=4→AB;
z=3x+4-4x=-x+4;
z'=(-x+4)'=-1≠0;
Границе OВ: y=x; z=3x+x –x*x=-x²+4x; z'=-2x+4; z'=0→ -2x+4=0; x=2; y=2. z min=z(0)=0, z min=z(B)=0; z max=z(A)=4; z max=z(M2)=4; (·)M2(2, 2).
6.Двойной интеграл. Основные понятия. Геометрический смысл двойного интеграла. Двойной интеграл. Пусть функция z= f(x, y) не отрицательная, не непрерывная, в замкнутой ограниченной областью, уравнение z = f(x, y) в пространстве определяется некоторую поверхность F, проекции которой на плоскость х, оу совпадает с областью Д. Тело ограниченное поверхностью, F с низу областью Д и вертикальной поверхность, в вдоль границы поверхности Д наз. криволинейный цилиндр. Выполним следующие действия:
1.
Разобьём область Д гладкими дугами
на n
частей Дi.
Обозначим S(Дi)
– площадь области Дi.
2. Выберем в каждой частной области Дi произвольную (·)Mi (xi, yi) и вычислим значение функции z в выбранных (·). Z (Mi) и составим сумму которая наз. интегральной суммой. Vn=f(M1)*S (Д1)+f(M2)*S (Д2)+…+f (Mn)*S (Дn) = Σn i=1f (Mi)*S (Дi). Каждое слагаемое f (Mi)*S (Дi) можно представить геометрически как объём малого цилиндра. Основание которого Дi, а высота f (Mi). Сумм Vn – есть сумма элементарных цилиндров. При увеличении количества Дi, то есть при n→∞, Vn→объёму криволинейного цилиндра. Расм. lim n→∞ Σn i=1f (Mi)*S (Дi). Опр.: Если сущ. этот предел независящий от способа разбиение области Д на часть Д и от выбора (·)Mi, то он наз.двойным интегралом от функции f(x, y) по области Д, то есть: lim n→∞ Σn i=1f (Mi)*S (Дi) = ∫∫д f(x, y)dxdy (1). Область д – наз. областью интегрирования, x, y – переменные интегрирования. dxdy=S(Дi) – элемент площади. Для какой функции сущ. двойной интеграл? Теорема: Если функция z= f(x, y) – непрерывна в замкнутой области Д, но она интегрируема в этой области. Геометрический смысл: Объём цилиндра ограниченное сверху z = f(x, y), снизу замкнутой областью, Д є x0y, с боков цилиндрический поверхность (криволинейный цилиндр). Произведём действие записанные в предыдущем пункте. Объём цилиндра Vi=f (Mi)*S (Дi).Объём криволинейной цилиндра Vкр.ц.= Σn i=1Vi – это равенство тем точнее, тем что чем меньше Дi, тем больше n. Vкр.ц.= lim n→∞ Σn i=1f (Mi)*S (Дi)= ∫∫д f(x, y)dxdy (2). Вывод: величина двойного интеграла от неотрицательной функции = объёму цилиндрического тела.
7.Физический смысл двойного интеграла. Свойства двойного интеграла. Масса плоской пластинки требуется найти массу М пластинки Д зная, что поверхностная плотность γ=γ(x,y) –непрерывная функция. Произведём действия из первого пункта. Произведение γ(xi, yi)*S(Дi), есть масса элементарной области mi, тогда m=lim n→∞Σmi; m= Σn i=1mi= lim n→∞ γ(xi, yi)*S(Дi)=∫∫д f(x, y)dxdy (3).Вывод: двойной интеграл от плотности γ(x,y), численно равен массе пластинки Д - физ. смысл. Основные свойства двойного интеграла: Пусть функция z1= f(x, y), z2= g(x, y) интегрируемы в области Д тогда: 1)∫∫Д c*f(x,y)dxdy=c∫∫Д f(x,y)dxdy, c=const; 2)∫∫[f(x,y)±g(x,y)]dxdy=∫∫Д f(x,y)dxdy± ∫∫Д g(x,y)dxdy 3)Если f(x, y)≥ ∫∫(x,y)dxdy∫≥0 4)Если область Д состоит из двух областей Д=Д1UД2, тогда ∫∫ Д f(x,y)dxdy =∫∫ Д1 f(x,y)dxdy+∫∫ Д2 f(x,y)dxdy 5)∫∫dxdy=S(Д) – одиночная функция 6)Если S – площадь области Д, то в этой области найдется (·)(x0,y0) токая, что ∫∫ Д f(x,y)dxdy=f(x0,y0)*S(Д) f0(x0,y0) –наз.средним значением функции f(x,y) в области Д. |
8. Вычисление двойного интеграла.
Требуется
вычислить двойной интеграл ∫∫Д
f(x,y)dxdy,
f(x,y)≥0.
Пусть область Д ограничена вертикальными
прямыми x=a,
x=b,
вертикальными y=φ1(x),
y=φ2(x),
причём y=φ2(x)>
y=φ1(x).
Пусть любая прямая || оси оу пересекает
область Д не более чем в двух точках,
такая область наз. правильная в
направлении оси оу, тогда справедлива
формула: ∫∫Д f(x,y)dxdy = ∫ab dx ∫ φ2(x) φ1(x). f(x, y) dy (4) – формула для вычисления двойного интеграла. В начале интегрируем f(x,y) по переменной у, считая x=const, а затем результат по переменной х, на отрезке [а,b]. Правая часть формулы (4) наз. повторным интегралом, от функции f(x,y). ∫ φ2(x) φ1(x). f(x, y) dy – наз. внутренним интегралом. ∫ab dx – наз. внешним интегралом. Фактически вычисление двойного интеграла сводиться к определению двух определенных интегралов. Если область Д ограничена прямыми y=c, y=d, функциям x=Ψ1(y), c=Ψ2(y) и область Д явл. правильной в направлении оси ох. ∫∫Д f(x,y)dxdy = ∫dc dy ∫ Ψ2(y) Ψ1(y). f(x, y) dx (5)
Здесь
при вычислении внутреннего интеграла
считаем у – постоянным. Замечание:
Пример неправильной области. Следует
разбить на конечное число правильных
областей проинтегрировать. Может
быть, что область Д такова, что одна
из функций задается двумя аналогичными
выражениями. То есть Тогда двойной интеграл ∫∫ Д=∫∫Д1+∫∫Д2. ∫∫Д f(x,y)dxdy =∫ca dx∫f(x,y)dy+∫bc dx ∫ φ2(y) φ1(y). f(x, y) dy. Замечание:
1.Формулы
(4) и (5) справедлива и для f(x,y)≤0; 2.Если область Д правильная в обоих направлениях то двойной интеграл можно вычислить по формуле (4) и по формуле (5) результат один и тот же. 3.Если область Д неправильная, то её надо разбить на части правильные в направлении оси ox или оси oy. 4.Внешние приделы в повторном интеграле всегда постоянные, а внутренние переменные или постоянные, зависит от области. Пр. Вычислить двойной интеграл. ∫∫Д (x²+y)dxdy; Д: y=x²; x=y²
9.Замена переменных в двойном интеграле. Переход к полярным координатам. Для упрощения вычисления двойного интеграла часто применяют метод подстановки, то есть водят новые переменные. Пусть требуется вычислить двойной интеграл по Д ∫∫Дf(x, y) dxdy, произведём замену по формулам. x=φ(u, v) y=Ψ(u,v) при этом область Д є плоскость xoy переходя в область G є пл. uov. Вычислим определитель который наз. якобиан. J = |ðx/ðu ðx/ðv ðy/ðu ðy/ðv| тогда справедлива формула замены переменной ∫∫Дf(x, y) dxdy= ∫∫Gf(φ(u,v), Ψ(u,v))|J| dudv (1) Наиболее распространенная система при вычисления двойного интеграла это полярные координаты (r, φ). Связь декартовых координат и полярных выражается формулами. x=r*cosφ, z≥0; y=r*sinφ, 0≤φ≤2π Пологая u=r, v=φ; вычислим якобиан: J = |ðx/ðr ðx/ðφ = |cosφ – r*sinφ = r*cos²φ+r*sin²φ=r; J=r; cos²φ+r*sin²φ=1 ðy/ðr ðy/ðφ| sinφ r*cosφ| Формула замен переменных будет иметь вид ∫∫Lf(x, y) dxdy= ∫∫Gf(r,φ)*r drdφ Область G в полярных координатах ограничена лучами φ=λ, φ=β и кривыми r=r1(φ)r=r2(φ). Область G правильная, т.к. лучь выходящий из полюса пересекает её границу не более чем в 2(·). Двойной интеграл в полярных сводят к повторному. ∫∫G f(r,y)*rdr*dφ = ∫βλ du ∫ r2(φ) r1(φ). f(r, φ) *rdr(2) Внешний интеграл всегда по φ в полярных координатах. Замечание: 1)Переход к полярным координатам полезен когда под интегральная функция имеет вид f(x²+y²), а область интегрирования есть круг, сектор, кольцо и т.д. 2)На практике преобразование области Д в область G не выполняют, а совмещают декартову и полярную системы координат и находят нужные пределы по r и φ.
11.Тройной интеграл. Основные понятия, свойства тройного интеграла. Теория тройного интеграла аналогично теории двойного интеграла поэтому рассмотрим её сокращённо. Пусть в замкнутой области V пространство охyz заданно непрерывна функция трёх переменных u=f(x, y, z): 1)Разобьем область V на n – частей Vi=i=1nˉ 2)Выберем в них произвольную (·) Mi (xi, y1, zi) 3)Вычислим значение функции u в (·)(Mi)=f(xi, yi, zi). 4)Составим интегральную сумму Σnn=1 f(xi, yi, zi)*ΔVi, где ΔVi – объём элементарной области Vi. Если сущ. предел экспериментальной суммы при n→∞ и он не зависит от выбора (·)Mi, то он наз. тройным интегралом от функции u=f(x,y.z), по области V. Обозначим: ∫∫∫Vf(x, y, z)dxdydz=limn→∞Σni=1 f(xi,yi,zi)*ΔVi (1) Свойства тройного интеграла: обладает тем же свойствами, что и двойной. 1)∫∫∫V с*f(x, y, z)dxdydz=с∫∫∫V f*dxdydz обозначим dxdydz=dv 2)∫∫∫V (f+g)dv=.∫∫∫V f*dv+∫∫∫V g*dv 3)∫∫∫V f*dv = =.∫∫∫V1 f*dv+∫∫∫V2 g*dv = V=V1UV2 4)если f (x,y,z)≥0, то ∫∫∫V f*dv≥0 5)∫∫∫V dv = V – объём тела V. 6) Теорема о среднем сущ. токая (·) M0 (x0, y0, z0) Є тему V, что ∫∫∫V fdv = f(x0, y0, z0) * Vт, Vт – объём тела.
10.Геометрические и физические приложения двойного интеграла. 1.Объём тела – из геометрического смысла двойного интеграла известно, что V тела =0. Vт=∫∫Д f(x, y) dxdy (3) Д – проекции тела на плоскость xoy. 2.Площадь плоской фигуры; Если в формуле (3) f(x, y)=1, то цилиндрическое тело превращается в прямой цилиндр с высотой H=1, V такого тела = площади основания Д, то есть ∫∫Д dxdy=SД в полярных координатах ∫∫Д rdrdφ=SД 3.Масса плоской пластинки из физического смысла двойного интеграла известно, что m=∫∫Д γ(x, y) dxdy, где γ(x, y) – поверхностная плотность пластины. 4.Статические моменты и координаты центра тяжести плоской фигуры. Статические моменты фигуры Д относительно осей ох и оу =(Sx=∫∫Д y*γ(x, y) dxdy, Sy=∫∫Д x*γ(x, y) dxdy); где γ(x, y) Координаты центра масс фигуры Д= xc=Sy/m; yc=Sx/m. Применение двойного интеграла не исчерпывается приведенными формулами они значительно шире. |
12.Вычисление тройного интеграла. Сводиться к вычислению 3 определенных интегралов. Пусть областью интегрирования V явл. тело ограниченное снизу поверхностью z=z1*(x, y), с верху z=z2*(x, y), причём z2> z1 проекции тела V на плоскость хоу явл. областью Д. V – правильная в направление оси oz, тогда для любой непрерывно функции Vx,y,z, заданно в области V имеет место формула. ∫∫∫Vf(x, y, z)dxdydz=∫∫Д(∫z1(x,y) z2(x,y)f(x, y, z) dz) dxdy (2) Если область Д ограничена линиями x=a, x=b, y=φ1x, y=φ2x, (φ2(x)≥φ1(x)), то формула (2) имеет вид.
∫∫∫V
f(x,
y,
z)dxdydz=∫abdx∫φ1(x)
φ2(x)dy∫z1(x,y)z2(x,y)
f(x,y,z)dy
(3) Тройной интеграл свели к повторным Замечание: 1)Если область V – сложное, то её надо разбить на конечное число просто правильных областей. 2)Порядок интегрирования в формуле (3) может быть любым.
13.Замена переменных в тройном интеграле. Цилиндрические координаты. Часто применяют метод подстановка. Пусть производиться подстановка x = φ(u, v,ω), y=Ψ(u,v,ω), z=&(u,v,ω), составим якобиан. J = |ðx/ðu ðx/ðv ðx/ðω ≠ 0 ðy/ðu ðy/ðv ðy/ðω ðz/ðu ðz/ðv ðz/ðω Справедлива формула замены переменных ∫∫∫Vf(x, y, z)dxdydz= ∫∫∫Vf(u, v, ω)*|J|dudvdω; Наибольшее удобно переходить к цилиндрическим координатам. Положение (·) М (x, y, z) в пространстве oxyz, можно определить заданием 3 чисел r, φ, z, где r – длина проекции радиуса вектора (·) M на плоскость xoy. φ – угол образований этой проекции с осью ох. z – опликата (·) М. Числа r, φ, z называется цилиндрическими координатами. Цилиндрические и декартовые координаты связаны по формулам: x=r *Cos φ; y = r*Sin φ; z = z r≥0, 0≤φ≤2π; z Є R Составим Якобиан для цилиндрических координат J = |Cos φ - r sin φ 0 = cos φ - r sin φ= r* Cos ²φ+r*Sin²φ=2 Sin φ r cosφ 0 sin φ r cos φ 0 0 1| Замечании: К цилиндрическим координатам удобно переходить когда область определение цилиндрическая поверхность.
14.Дифференциальные уравнения I порядка. Основные понятия. Задача Коши. Основные понятия: Соотношение (F(x, y,y'…yⁿ)=0 (1) Связываем x, y и производные y' – наз. ДУ. Если уравнение (1) можно записать в форме yⁿ=f(x, y, y',…yn-1) (2) говорят, что ДУ решено относительно старшей производной или ДУ в нормальной форме. ДУ в катаром функции у зависит от одной переменной наз. обыкновенной (ОДУ). Если ДУ зависит от нескольких переменных, то имеет диф. уравнений в частных производными. Мы будем расм. ОДУ. Порядок ДУ определяется наивысшей производной входящей в ДУ. Решение или интегралом ДУ наз. такая функции y=y(x), что при подстановке в уравнении (1) вместе с производными получаем тождество. Всякому решение ДУ на плоскости соответствует некоторая кривая y=y(x),которая наз. интегральной кривой. Процесс нахождения решения ДУ наз. интегрированием ДУ. ДУ имеет бесчисленное множество решений. ДУ I первого порядка. Общий вид F (x, y, y')=0 (3) В нормальной форме y'=f(x,y) (4) Общим решением уравнения (3) наз. функция y=y(x, C) удовлетворяющая условия: 1) y(x, C) – непрерывная дифференцируема на (a, b). 2). y'=f(x, C) – при подстановке y и y' в уравнении получаем тождество. Уравнение (3) или (4) имеет бесчисленнее количество решений, что бы выделить одно, частное решение надо задать начальное условие y(x0)=y0 (5) или условие Каши. Задача Коши: найти частное решение ДУ (4), удовлетворяющие начальному условию (5). С геометрической (·) зрения общее решение y=y(x, c) есть семейство интегральных кривых на плоскости xoy. Частное решение y=y(x, C0) одна из кривых проходящая через заданную (·)(x0, y0).
15.Дифференциальные уравнения с разделяющимися переменными. Однородные Дифференциальные уравнения. ДУ с разделяющими переменными y'=f(x)*g(y) – общий вид dy/dx=f(x)*g(x) – умножим на дробь dx/g(x); dy/dx*dx/g(xy)=f(x)*g(y)*dx/g(y) dy/g(y)=f(x)*dx – интегрируем обе части этого равенства и получим общее решение. ∫dy/g(y)=∫f(x)dx, dy – может быть представив в дифференциальной форме ДУ с разделив переменные. M (x, y) dx + N(x, y) dy=0; Пр. Решить ДУ. xdy-2ydx=0; xdy=2ydx разделить 1/x*y, x≠0, y≠0; dy/y=2*dx/x; ∫dy/y=2∫dx/x; ln|y|=2ln|x|+ln|C|; ln|y|=ln|x²*C| y=C*x² - параболы их множества. Одинарные ДУ – функция f(x,Y) наз. однородной функцией нулевого измерения если при умножении аргументов z и y, на произвольный параметре t, значение функции не измениться. Однородное функция может быть записана в виде f(x,y)=φ(1;y/x) Пр. Дана функция f(x,y)=x+y/x-y умножим x и y на t. f(tx,ty)=tx+ty/tx-ty=t(x+y)/t(x-y)=x+y/x-y – это однородная функция однородного измерения. Разделим числитель и знаменатель на х. f(x,y)=(x+y/x)/(x-y/x)=(1+y/x)/(1-y/x)=φ(1;y/x). Функции f(x,y) наз. однородной функции n – измерение если, при замене x и y на х→tx; y→ty, получается тоже функция умноженная на tⁿ, то есть f(tx,ty)=tⁿf(x,y) Уравнение вида y'=φ(1; y/x) (6) или M(x,y)dx+N(x,y)dy=0 (7) наз. однородными, где M и N однородные функции одного измерения. Уравнение (6) и (7) приводиться к уравнению с разделяющимися переменной заменой. y/x=u(x); y=u(x)*x; y'=u'(x)*x+u(x) y и y' подставляется в уравнении (6). Замечание: Иногда однородное уравнения удобно интегрировать считая х, функцией от у, тогда производиться замена x/y=u(y).
22.Линейные неоднородные дифференциальные уравнения высших порядков с постоянными коэффициентами. Структура общего решения.
Линейные
неоднородные дифференциальные
уравнения с постоянными коэффициентами.
Общий вид:
Теорема:
Общее решение неоднородного уравнения
равно сумме общего решения соответствующего
однородного уравнения и частного
решения неоднородного уравнения,
т.е.:
Общее
решение однородного уравнения:
|
16.Линейные Дифференциальные уравнения I порядка. Решение методом Бернулли. Линейные ДУ I порядка. Общий вид такого уравнения y'+P(x)*y=Q(x) (8). Это уравнение линейное относится y и y'. Если Q(x)=0, то уравнение (8) наз. линейное однородное уравнение. y'+P(x)*y=0 (9) – уравнение с разделяющими переменными, если Q(x)≠0, то линейное уравнение не однородное. Сущ. несколько методов решения уравнения (8). Один из методов метод подстановки Бернулли. Он закл. в том, что решение уравнения (8) запишем в виде y=u(x)*v(x), где u и v непрерывные дифференцируемые функции. y'=u'v+uv'. Подставим y и y' в уравнение (8) u'v+uv'+P(x)*u*v=G(x) сгруппируем uv'+v(u'+P(x)v)=Q(x) (*) В качестве функции u от x возьмём решение уравнения u'+P(x)v=0 – уравнение с разделяющимися переменными. du/dx=-P(x)*u разделить dx/u; du/u=-P(x)dx интегрируем обе части ∫du/u=-P(x)dx; ln|u|=-∫P(x)dx+C1. Здесь в качестве C1=0, для упрощения вычисления в дальнейшем Выразим (u) проинтегрируем обе части. u =e -∫P(x)dx. Подставим в уравнение (*) e -∫P(x)dx.*v=Q(x); e -∫P(x)dx.*dv/dx=Q(x) | dx*e -∫P(x)dx dv=Q(x)* e -∫P(x)dx dx интегрируем обе части v=∫Q(x) e -∫P(x)dx dx +C Общее решение неоднородного уравнения (yон) yон= u(x)*v(x)= e -∫P(x)dx (Q(x) e ∫P(x)dx dx+C).
17.Линейные ДУ I порядка. Решение методом вариации произвольной постоянной. Линейные ДУ I порядка. Общий вид такого уравнения y'+P(x)*y=Q(x) (8). Это уравнение линейное относится y и y'. Если Q(x)=0, то уравнение (8) наз. линейное однородное уравнение. y'+P(x)*y=0 (9) – уравнение с разделяющими переменными, если Q(x)≠0, то линейное уравнение не однородное. Сущ. несколько методов решения уравнения (8). Один из методов метод вариации постоянной (Метод Лагранжа): суть метода находим общее решение линейного однородного уравнения. y'+P(x)y=0 d/dx=-P(x)y; dy/y=-P(x)dx; -ln|C|+ln|y|=-∫P(x)dx; ln|y/c|=-∫P(x)dx; y/c= e -∫P(x)dx; y0=C* e ∫P(x)dx – решение однородного уравнения. Заменим С на функцию С(х) и yон=С(х)*e ∫P(x)dx . Чтобы найти С(х) подставим yон в у равнение y'он=С'(х)* e ∫P(x)dx + С(х)* e ∫P(x)dx (-Рх))=Q(x) (∫f(x)dx)'=f(x); С'(х)* e ∫P(x)dx - P(x) * С(х)* e ∫P(x)dx +P(x)*C(x)* e -P(x)dx ; C'(x)* e -P(x)dx =Q(x); C'(x) = Q(x)* e ∫P(x)dx ; dc/dx=Q(x)* e ∫P(x)dx ; C(x)=∫Q(x)*e∫P(x) dx+C1. Подставим С(х) в уон и получим решение.
18.Дифференциальные уравнения I порядка Бернулли. Дифференциальные уравнения высших порядков. Основные понятия. Задача Коши. Линейные ДУ I порядка. Общий вид такого уравнения y'+P(x)*y=Q(x) (8). Это уравнение линейное относится y и y'. Если Q(x)=0, то уравнение (8) наз. линейное однородное уравнение. y'+P(x)*y=0 (9) – уравнение с разделяющими переменными, если Q(x)≠0, то линейное уравнение не однородное. Сущ. несколько методов решения уравнения (8).Один из методов уравнение Бернулли. y'+P(x)y=Q(x)*ym (10). Если m=0, то получаем ЛДУ, если m=1, то получаем уравнение с разделяющимися переменными. Расм. когда m≠0; 1. Разделим уравнение (10) на ym, получаем . y'/ ym +P(x)y/ ym =Q(x); y'*y-m+P(x)*y1-m =Q(x) сделаем замену y1-m =z(x) продифференцируем (1-m) y-m* y'=z'; y' y-m=(1/1-m)*z'подставим в уравнение (1/1-m)*z'+P(x)*z=Q(x) – получим линейное ДУ I. Линейное относительно функции z. Замечание: Уравнение Бернулли можно решать и подстановкой Бернулли. ДУ высших порядков Осн. понятия: F(x, y, y', y'',…yⁿ)=0 (1) –ДУ n -порядка. yⁿ=f(x, y), y', y''…y(n-1) (2) – решенное относительно старшей производной. Общее решение ДУ n-порядка зависит от n-произвольных постоянных С1, С2, Сn .Решение ДУ I.или II имеет вид y=φ(x, C1, C2,..Cn) – общее решение в явл. виде φ(x, у, C1, C2,..Cn)=0 – общий интеграл (в не явл. виде) Геометрически общее решение представляет семейство интегральных кривых на плоскости хоу, зависящие от n –параметров C1, C2,..Cn . Для вида частного решения требуется задание значений функции и её n-1 производных в (·)х0, то есть y(х0)=y0; y'(х0)=y01; y''(х0)=y02;. y (n-1)(х0)=y0 (n-1) (3); где y0 , y01, y02 – задание числа. Задача Каши: Найти частное решение уравнения (1) или (2) удовлетворяющее системе начальных уравнений (3). 19.Дифференциальные уравнения высших порядков, допускающие понижение порядка (3 типа).
1.Общий
вид:
Порядок
уравнения понижается каждый раз на
единицу путем последовательного
интегрирования.
……………………………………
2.Д.У
не содержащие явно искомой функции y
и ее первых производных до порядка
Производится
замена:
…………………
Уравнение
(2) сводится к:
3.Д.У. не содержащие явно независимой переменной x. Общий вид:
Производится
замена:
Порядок уравнения понижается на единицу. |
||||||||||||||||||||||||||||||||
|
20.Линейные однородные дифференциальные уравнения высших порядков с постоянными коэффициентами. Характеристическое уравнение. Решение для случая действительных различных корней.
Линейные
однородные Д.У. высших порядков с
постоянными коэффициентами (ЛОДУ).
Общий вид:
Решение
уравнения (1) будем искать в виде:
где
Дифференцируем
последовательно решение (2):
……………..
Подставим y и производные в уравнение (1):
Сократим
на
Функция
Уравнение
(3) называется характеристическим
уравнением для уравнения (1) оно
получается из Д.У. (1) путем замены
производной на соответствующую степень
числа
………………..
Таким
образом, чтобы найти решении Д.У. (1)в
виде (2) нужно: 1)Составить
характеристическое уравнение (3);
2)Найти
его корни
Возможны следующие случаи корней характеристического уравнения: 1)Корни действительные и различные; 2)Корни действительные кратные; 3)Корни комплексные различные; 4)Корни комплексные кратные;
Корни
действительные различные:
Пусть
.………….
Эти
функции линейно независимые и образуют
фундаментальную систему решений.
Линейная комбинация этих функций
является общим решением уравнения
(1):
21.Решение линейных однородных дифференциальных уравнений для случая комплексных и кратных корней.
Корни
действительные кратные:
Пусть
……………..
Общее уравнение:
Корни
комплексные различные:
среди корней есть пара комплексных
сопряженных, т.е.
Общее решение однородного уравнения для комплексных корней:
Корни
комплексные кратные:
Пусть корни
23.Нахождение частного решения линейных неоднородных дифференциальных уравнений с постоянными коэффициентами по специальному виду правой части.
Нахождение
частного решения по специальному виду
правой части уравнения
Замечание:
Если
функция f(x)
содержит несколько слагаемых, каждая
из которых приложит одному из приведенных
в таблице видов, то частное решение
ищется в соответствии с принципом
суперпозиции, т.е.:
|
24.Знакоположительные числовые ряды. Ряд геометрической прогрессии.
Числовые
ряды
– рассмотрим числовую последовательность:
Составим
суммы:
…………………..
Выражение:
Числа
Числовой
ряд (1) называется сходящимся,
если последовательность частичных
сумм сходится к некоторому числу S,
которое называется суммой ряда, т.е.
ряд сходится если существует предел:
Ряд
геометрической прогрессии
– Исследуем на сходимость ряд:
геометрической
прогрессии.
Сумму первых n-членов
ряда геометрической прогрессии находим
по формуле:
Найдем
Рассмотрим следующие случаи:
1)
2)
3)
Вывод:
ряд геометрической прогрессии (2)
сходится, при
25.Свойства числовых рядов. Необходимые условия сходимости ряда. Простейшие свойства числовых рядов:
1.Суммой
двух рядов
2.Произведением
ряда на действительное число α
называется ряд:
3.Сходимость ряда не нарушается, если произвольно изменить (переставить, добавить или отбросить) конечное число членов. Сумма может измениться;
4.Сходящийся
ряд можно почленно умножать на любой
множитель α,
и если сумма ряда равна
5.Сходящиеся
ряды можно почленно складывать и
вычитать:
Необходимое условие сходимости ряда:
Теорема:
Если
ряд
Доказательство:
Если ряд
Если
условие (1) не выполняется, то ряд
расходится. Условие (1) не является
достаточным условием сходимости ряда,
т.е. из выполнения равенства
26.Достаточные признаки сходимости: признак Даламбера, радикальный признак Коши. Необходимый признак сходимости не дает, вообще говоря, о том сходится ряд или нет. Сходимость и расходимость ряда можно установить с помощью достаточных признаков.
Признак
Даламбера
– пусть дан ряд
Радикальный
признак Коши
– дан знакоположительный ряд
27.Достаточный признак сходимости: интегральный признак Коши. Сходимость обобщённого гармонического ряда. Необходимый признак сходимости не дает, вообще говоря, о том сходится ряд или нет. Сходимость и расходимость ряда можно установить с помощью достаточных признаков.
Интегральный
признак Коши
– дан знакоположительный ряд
…………..
тогда:
1.Если
несобственный интеграл:
2.Если
несобственный интеграл:
Замечание
(о сходимости несобственного интеграла):
Обобщенный гармонический ряд:
Ряд
(1) называется рядом Дирихле. Исследуем
ряд на сходимость по интегральному
признаку. Рассмотрим функцию
Вывод:
ряд Дирихле
при
Этот ряд удобно использовать в признаках сравнения.
|
28.Знакопеременные и знакочередующиеся ряды. Признак Лейбница. Свойства абсолютно и условно сходящихся рядов.
Ряд
вида:
Остатком
ряда (1) называется сумма:
Теорема (Признак Лейбница) – дан знакочередующий ряд (1), тогда если:
1.Члены
ряда убываю по абсолютному значению
начиная с некоторой последовательности:
2.Предел
То
ряд (1) сходится и его сумма не превосходит
1-ого члена ряда
Ряд
удовлетворяющий теореме Лейбница
называется рядом Лейбница. Неравенство
Свойства
абсолютно и условно сходящихся рядов:
Пусть даны два ряда
1)Ряд
2)Ряд
3)Пусть
ряда
4)Если
ряд
5)Если
ряд
29.Функциональные
ряды. Область сходимости. Сходимость
ряда
Ряд
Ряд (1) называется функциональным, т.к. его члены являются функциями от x. Давая x определить числовые значения мы получим различные числовые ряды, которые могут сходится или расходится. Определение: Совокупность тех значений x, при которых функциональный ряд сходится, называется областью сходимости этого ряда. Сумма ряда обозначается S(x) и она является функцией от (x).
30.Степенные
ряды
Среди функций рядов особую роль играют ряды, членами которых являются степенные функции. Определение: Степенным рядом называется функция ряда вида:
Рассмотрим ряд:
Ряд
(2) – степенной ряд со степенями
Теорема Абеля:
1.Если
степенной ряд (1) сходится, при некотором
значении
2.Если
степенной ряд (1) расходится, при
некотором значении
Поясним теоремы:
1.Если
ряд (1) сходится в точке
2.Если
ряд расходится в точке
Вывод: Область сходимости степенного ряда (1) является интервал конечный и бесконечный с центром в точке O или единственная точка O.
Положим
Если
степенной ряд сходится лишь в одной
точке
Для
нахождения радиуса сходимости
степенного ряда (1) можно использовать
признак Даламбера или признак Коши.
Допустим, что существует предел:
Аналогично рассуждаем, если применить признак Коши, тогда радиус:
Замечание:
Интервал сходимости степенного ряда
(2) находят из неравенства
|
31.Разложение функций в степенные ряды. Ряд Тейлора. Ряд Маклорена.
1.Ряд
Тейлора
– Если функция f(x)
имеет производные любых порядков в
окрестности точки
(1) – называется рядом Тейлора.
Если
в формуле (1) положить
Формулу
(1) можно записать в виде:
где
Ряд
Тейлора можно формально записать для
любой бесконечно дифференцируемой
функции в окрестности точки
Теорема:
Для того чтобы ряд Тейлора (1) функции
f(x)
сходится к функции f(x)
в точке x
необходимо и достаточно, чтобы в этой
точке остаточный член
Задача
разложения функции f(x)
в степенной ряд сводится к определению
значений x,
при которых
2.Разложение некоторых элементарных функций в ряд Маклорена – для разложение функции f(x) в ряд Маклорена (2) надо:
1.Найти
производные f
2.Вычислить
их значение в точке
3.Подставить в ряд (2); 4.Найти интервал сходимости ряда ли найти интервал (-R,R), в котором остаточный член ряда стремится к нулю. Эти интервалы совпадают; Таблица основных разложений элементарных функций в ряд Маклорена:
1.
2.
3.
4.
5.
6.
7.
32.Разложение в ряд Маклорена функций еx , sin x.
1.Находим
производные:
…………….
2.Вычислим
значение функции в 0:
……………
3.Подставляем
в ряд Маклорена:
4.Находим
радиус сходимости:
1.
…………………………………..
2.
……………
3.
4.
33.Приложение степенных рядов. Приближенное вычисление значений функций. Вычислить sin1 с точностью δ= 10-3.
Приближенное
значение вычисление значений функции:
Пусть требуется вычислить значение
функции f(x),
при
Вычислить sin1 с точностью δ= 10-3:
Сравним
каждый ряд с
|
34.Приложение
степенных рядов. Приближенное вычисление
интегралов. Вычислить интеграл
Приближенное
вычисление интегралов:
В теории вероятностей большое значение
имеет интегральная функция Лапласса:
Для нее составлены таблицы значений. Вычислим значение функции Лапласса с помощью разложения в ряд подинтегральной функции при x = 0,5, с точностью δ= 10-3 и сравним с табличным.
Из
таблицы
35.Тригонометрический ряд Фурье. 2П – периодическая функция. Теорема Дирихле. Тригонометрическим рядом называется ряд вида:
Теорема
Дирихле (достаточные условия разложения
функции в ряд Фурье):
Пусть
1.f(x) – кусочно-непрерывная, т.е. непрерывная или имеет конечное число разрывов первого рода; 2.f(x) – кусочно-монотонна, т.е. монотонна на всем отрезке или этот отрезок можно разбить на конечное число интервалов, что на каждом из них функция монотонна, тогда соответствует функции f(x) ряд Фурье сходится на этом отрезке и при этом: 1.в точках непрерывности функции, сумма ряда S(x) совпадает с самой функцией, т.е. S(x) = f(x);
2.в
каждой точки разрыва функции, сумма
ряда равна:
3.на
концах интервала, т.е. в точках
Вывод:
Если функция f(x)
удовлетворяет условиям 1
и 2
теоремы Дирихле, то на отрезке [- Замечания:
1.Если
функция f(x)
с периодом
2.Условия Дирихле удовлетворяют большинство функций встречающихся в математике;
36.Разложение в ряд Фурье чётных и не чётных функций.
Если
Из свойства определенного интеграла известно: Если функция f(x) интегрируется на симметричном отрезке [-a;a], то:
Рассмотрим случаи:
1.Если
f(x)
– четная, то
2.Если
f(x)
– нечетная, то
Следовательно:
1.Если
f(x)
– четная, то:
Тогда
коэффициенты Фурье имеют вид:
Ряд
Фурье для четной функции f(x)
имеет вид:
2.Если
f(x)
– нечетная, тогда:
Коэффициенты
Фурье:
Ряд
Фурье для нечетной функции:
Ряды (1) и (2) называются по косинусам и синусам.
|
||||||||||||||||||||||||||||||||
|
37.Разложение в ряд Фурье функций произвольного периода.
Разлагать
в ряд Фурье можно и периодическую
функцию с периодом от
Пусть
функция f(x),
определенная на отрезке [
т.е.
Разложение
функции
где
Возвращаясь
к переменной x
и заметив, что
(1)
где (2)
Ряд
(1) с коэффициентами вычисляемыми по
формулам (2) называются рядо Фурье для
функции f(x)
с периодом
Замечание:
Все теоремы имеющие место для рядов
Фурье
где
Если
f(x)
– нечетная функция, то
где
|
1.Функция двух переменных. Определение. Геометрическое изображение. 2.Частные производные первого порядка функции двух переменных. Геометрический смысл. 3.Частные производные высших порядков функции двух переменных. 4.Экстремум функции двух переменных. 5.Наименьшее и наибольшее значения функции двух переменных в замкнутой области. 6.Двойной интеграл. Основные понятия. Геометрический смысл двойного интеграла. 7.Физический смысл двойного интеграла. Свойства двойного интеграла. 8.Вычисление двойного интеграла. 9.Замена переменных в двойном интеграле. Переход к полярным координатам. 10.Геометрические и физические приложения двойного интеграла. 11.Тройной интеграл. Основные понятия, свойства тройного интеграла. 12.Вычисление тройного интеграла. 13.Замена переменных в тройном интеграле. Цилиндрические координаты. 14.Дифференциальные уравнения I порядка. Основные понятия. Задача Коши. 15.Дифференциальные уравнения с разделяющимися переменными. Однородные Дифференциальные уравнения. 16.Линейные Дифференциальные уравнения I порядка. Решение методом Бернулли. 17.Линейные ДУ I порядка. Решение методом вариации произвольной постоянной. 18.Дифференциальные уравнения I порядка Бернулли. Дифференциальные уравнения высших порядков. Основные понятия. Задача Коши. 19.Дифференциальные уравнения высших порядков, допускающие понижение порядка (3 типа). 20.Линейные однородные дифференциальные уравнения высших порядков с постоянными коэффициентами. Характеристическое уравнение. Решение для случая действительных различных корней. 21.Решение линейных однородных дифференциальных уравнений для случая комплексных и кратных корней. 22.Линейные неоднородные дифференциальные уравнения высших порядков с постоянными коэффициентами. Структура общего решения. 23.Нахождение частного решения линейных неоднородных дифференциальных уравнений с постоянными коэффициентами по специальному виду правой части. 24.Знакоположительные числовые ряды. Ряд геометрической прогрессии. 25.Свойства числовых рядов. Необходимые условия сходимости ряда. 26.Достаточные признаки сходимости: признак Даламбера, радикальный признак Коши. 27.Достаточный признак сходимости: интегральный признак Коши. Сходимость обобщённого гармонического ряда. 28.Знакопеременные и знакочередующиеся ряды. Признак Лейбница. Свойства абсолютно и условно сходящихся рядов.
29.Функциональные
ряды. Область сходимости. Сходимость
ряда
30.Степенные
ряды
31.Разложение функций в степенные ряды. Ряд Тейлора. Ряд Маклорена. 32.Разложение в ряд Маклорена функций еx , sin x. 33.Приложение степенных рядов. Приближенное вычисление значений функций. Вычислить sin1 с точностью δ= 10-3.
34.Приложение
степенных рядов. Приближенное вычисление
интегралов. Вычислить интеграл
35.Тригонометрический ряд Фурье. 2П – периодическая функция. Теорема Дирихле. 36.Разложение в ряд Фурье чётных и не чётных функций. 37.Разложение в ряд Фурье функций произвольного периода. |
|
|
|






 (1)
(1) ,
где
,
где
 –
решения однородного уравнения,
–
решения однородного уравнения, – частного решения неоднородного
уравнения.
– частного решения неоднородного
уравнения. .
. (1)
(1)


 включительно, т.е. общий вид
включительно, т.е. общий вид (2)
(2) ;
; ;
; ;
; .
Порядок, которого
.
Порядок, которого
 .
Решив его находим функцию
.
Решив его находим функцию
 ,
т.е. уравнение (1).
,
т.е. уравнение (1). (3)
(3) ;
; ;
; ….;
….; (1)
(1) – постоянные
числа или коэффициенты уравнения.
– постоянные
числа или коэффициенты уравнения. ,
(2)
,
(2) -
некоторое число, предложено Эйлером.
-
некоторое число, предложено Эйлером. ;
;


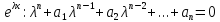 (3)
(3) является
уравнением решения (1) тогда и только
тогда когда число
является
уравнением решения (1) тогда и только
тогда когда число
 есть корень уравнения (3).
есть корень уравнения (3). ,
т.е.:
,
т.е.:
 ;
; ;
; ;
; ,
,
 ,…,
,…,
 ;
3)Каждому
корню соответствует решение:
;
3)Каждому
корню соответствует решение:
 ;
;
 ;
; ,
,
 ,…,
,…,
 - действительные различные корни
уравнения (3) им соответствует n-решений:
- действительные различные корни
уравнения (3) им соответствует n-решений:
 ;
; ;
; ;
; (4)
(4) - корень уравнения
- корень уравнения
 кратности
R,
тогда решениями Д.У.
кратности
R,
тогда решениями Д.У.
 является
k
–
линейно независимых функций:
является
k
–
линейно независимых функций:
 ;
; ;
; ;
; ;
; (1)
(1) .
Этой паре соответствуют две действительные
функции:
.
Этой паре соответствуют две действительные
функции:
 ;
; ;
; (2)
(2) кратности
k,
тогда общее решение Д.У. имеет вид:
кратности
k,
тогда общее решение Д.У. имеет вид: (3)
(3) функции f(x):
Вид частных решений запишем в таблицу:
функции f(x):
Вид частных решений запишем в таблицу: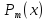






 не является корнем характеристического
уравнения
не является корнем характеристического
уравнения
 является корнем характеристического
уравнения кратности k
является корнем характеристического
уравнения кратности k

 не
является корнем характеристического
уравнения
не
является корнем характеристического
уравнения
 является
корнем характеристического уравнения
кратности k
является
корнем характеристического уравнения
кратности k
 – многочлен
степени m
с неопределенными коэффициентами;
– многочлен
степени m
с неопределенными коэффициентами;
 ;
;
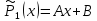 ;
;
 ;
;
 ….
A,B,C,D
– неопределенные коэффициенты, которые
нужно найти.
….
A,B,C,D
– неопределенные коэффициенты, которые
нужно найти.
 un
– числа.
un
– числа. ;
; ;
; ;
; – называется числовым рядом
(1)
– называется числовым рядом
(1) - называются
членами ряда. Если они положительны,
то ряд называется знакоположительным.
- называются
членами ряда. Если они положительны,
то ряд называется знакоположительным. -
называется n-ый
член ряда или общий член ряда.
-
называется n-ый
член ряда или общий член ряда. -
частичные суммы.
-
частичные суммы. .
Если предел не существует или равен
бесконечности, то ряд называется
расходящимся.
Ряд может быть задан перечислением
нескольких членов или в виде формулы
общего члена ряда.
.
Если предел не существует или равен
бесконечности, то ряд называется
расходящимся.
Ряд может быть задан перечислением
нескольких членов или в виде формулы
общего члена ряда. Этот ряд называется рядом
(2)
Этот ряд называется рядом
(2) ,
,


 ,
тогда
,
тогда
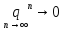 ,
поэтому
,
поэтому
 –
ряд сходится;
–
ряд сходится; ,
тогда
,
тогда
 ,
и
,
и
 -
ряд расходится;
-
ряд расходится; ,
тогда ряд (2) имеет вид:
,
тогда ряд (2) имеет вид:
 ,
его сумма
,
его сумма
 ,
,
 - ряд расходится;
- ряд расходится; и
и
 его и расходится, при
его и расходится, при
 .
. и
и
 называется ряд
называется ряд
 ;
; ;
; ,
то сумма
,
то сумма
 ;
; ;
;
 ,
то
,
то
 ;
; сходится, то его общий член
сходится, то его общий член
 ,
т.е.
,
т.е. (1)
(1)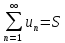 ,
,
 .
Запишем:
.
Запишем:
 и найдем его предел
и найдем его предел
 ч.т.д.
ч.т.д. не обязательно вытекает сходимость
ряда.
не обязательно вытекает сходимость
ряда. знакоположительный и существует
предел отношения последнего члена
ряда к предыдущему, т.е.:
знакоположительный и существует
предел отношения последнего члена
ряда к предыдущему, т.е.:
 ,
тогда, если
,
тогда, если
 .
. ,
если существует предел
,
если существует предел
 ,
тогда если
,
тогда если
 .
. ,
пусть его члены могут быть представлены
как числовые значения некоторой
функции f(x),
которая убывает на промежутке [1;+∞),
т.е.:
,
пусть его члены могут быть представлены
как числовые значения некоторой
функции f(x),
которая убывает на промежутке [1;+∞),
т.е.:
 ;
; ;
; ;
; сходится, то и ряд сходится;
сходится, то и ряд сходится; расходится, то и ряд расходится;
расходится, то и ряд расходится; интеграл сходится, если lim
= ∞,
или не существует, интеграл расходится.
интеграл сходится, если lim
= ∞,
или не существует, интеграл расходится. ,
где p>0
– действительное число
(1)
,
где p>0
– действительное число
(1) ,
,
 это функция убывает на интервале (1;
это функция убывает на интервале (1;
 ).
).




 (1)
(1) (2)
(2)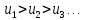 (3)
(3)
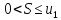 - остаток ряда удовлетворяет неравенство
- остаток ряда удовлетворяет неравенство
 .
. дает оценку остатка ряда Лейбница.
дает оценку остатка ряда Лейбница. и
и
 ,
они сходятся абсолютно к
,
они сходятся абсолютно к
 ;
;
 ,
тогда:
,
тогда: ;
; ,
(где α
– действительное число);
,
(где α
– действительное число); – сходится
условно,
тогда оба ряда полученных только из
положительных и только из отрицательных
членов этого ряда расходятся;
– сходится
условно,
тогда оба ряда полученных только из
положительных и только из отрицательных
членов этого ряда расходятся; – сходится
абсолютно
и его сумма равна A,
то при перестановке его членов ряд
остается сходящимися и его сумма не
меняется;
– сходится
абсолютно
и его сумма равна A,
то при перестановке его членов ряд
остается сходящимися и его сумма не
меняется; – сходится
условно,
то наперед заданного числа C,
существует перестановка членов ряда,
такая, что сумма полученного ряда
равна C.
– сходится
условно,
то наперед заданного числа C,
существует перестановка членов ряда,
такая, что сумма полученного ряда
равна C. .
. (1)
(1) – это
ряд геометрической прогрессии, со
знаменателем q
= x.
Ряд сходится
– это
ряд геометрической прогрессии, со
знаменателем q
= x.
Ряд сходится
 ,
т.е.
,
т.е.
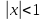 или
или
 -
область сходимости.
-
область сходимости.
 ,
,
 .
. .
Теорема Абеля. Интервал и радиус
сходимости степенного ряда.
.
Теорема Абеля. Интервал и радиус
сходимости степенного ряда. (1)
(1) -
постоянные числа, называются коэффициенты
ряда.
-
постоянные числа, называются коэффициенты
ряда. -
действительная переменная.
-
действительная переменная. (2)
(2)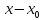 ,
,
 –
некоторое число. Ряд (2) сводится к ряду
(1) заменой:
–
некоторое число. Ряд (2) сводится к ряду
(1) заменой:
 .
Поэтому будем рассматривать только
ряд (1). Выясним вопрос о сходимости
ряда (1).
.
Поэтому будем рассматривать только
ряд (1). Выясним вопрос о сходимости
ряда (1). ,
то абсолютно сходится при всяком
значении x,
для которого
,
то абсолютно сходится при всяком
значении x,
для которого
 ;
; ,
то он расходится при всяком x
удовлетворяющем неравенству
,
то он расходится при всяком x
удовлетворяющем неравенству
 ;
; ,
то он абсолютно сходится в интервале
(
,
то он абсолютно сходится в интервале
( ;
; )
с центром в точке O;
)
с центром в точке O; ,
то он расходится в интервалах
,
то он расходится в интервалах
 .
Отметим это на числовой прямой:
.
Отметим это на числовой прямой: ,
тогда интервал сходимости будет
(-R,R).
Число R
называется радиусом сходимости
степенного ряда, т.е. это такое число,
что при всех
,
тогда интервал сходимости будет
(-R,R).
Число R
называется радиусом сходимости
степенного ряда, т.е. это такое число,
что при всех
 степенной сходится абсолютно, а при
всех
степенной сходится абсолютно, а при
всех
 расходится.
расходится. ,
то считаем
,
то считаем
 .
Если ряд сходится при всех
.
Если ряд сходится при всех
 ,
то считаем
,
то считаем
 .
На концах интервала, т.е. при
.
На концах интервала, т.е. при
 сходимость проверяется отдельно.
сходимость проверяется отдельно. .
Тогда по признаку Даламбера имеем:
.
Тогда по признаку Даламбера имеем:
 ,
тогда ряд сходимости для всех
,
тогда ряд сходимости для всех
 .
Таким образом, радиус сходимости можно
найти:
.
Таким образом, радиус сходимости можно
найти:
 (3)
(3) (4)
(4) и он имеет вид
и он имеет вид
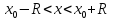 .
. ,
то можно записать разложений функций
f(x)
по степеням (
,
то можно записать разложений функций
f(x)
по степеням (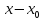 ):
):
 (1)
(1) ,
то получим разложение по степеням x,
которая называется рядом
Маклорена,
т.е.:
,
то получим разложение по степеням x,
которая называется рядом
Маклорена,
т.е.: (2)
(2) ,
,
 ,
,
 -
многочлен
Тейлора,
-
многочлен
Тейлора,
 ,
,
 ,
,
 -
остаточный член ряда Тейлора, записанный
в форме Лагранжа.
(3)
-
остаточный член ряда Тейлора, записанный
в форме Лагранжа.
(3) ,
однако он может быть расходящимся или
сходится, но не к функции f(x).
,
однако он может быть расходящимся или
сходится, но не к функции f(x). формула (3) стремился к нулю при
формула (3) стремился к нулю при
 .
.
 (4)
(4) стремится к нулю. Если это сделать
непросто, то следует использовать
другой способ, например применить
признак Даламбера и Коши.
стремится к нулю. Если это сделать
непросто, то следует использовать
другой способ, например применить
признак Даламбера и Коши. (x),
f
(x),
f (x)
и т.д. fn(x);
(x)
и т.д. fn(x); ;
; ,
,
 ;
; ,
,
 ;
; ,
,
 ;
; ,
,
 ;
; ,
,
 ;
; ,
,
 ;
; ,
,
 ;
; :
: ;
; ;
;
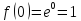 ;
; ;
; ;
; ;
; ;
; ;
Интервал сходимости
;
Интервал сходимости
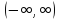 .
. :
: ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
Интервал
;
Интервал
 .
. ,
с заданной точностью
,
с заданной точностью
 .
Если функцию f(x)
в интервале (-R,R)
можно разложить в степенной ряд:
.
Если функцию f(x)
в интервале (-R,R)
можно разложить в степенной ряд:
 и
и
 ,
т.е.
,
т.е.
 ,
то точное значение
,
то точное значение
 сумме
этого ряда, а приближенное значение
равно частичной сумме этого ряда
сумме
этого ряда, а приближенное значение
равно частичной сумме этого ряда
 .
Точность этого равенства увеличивается
с ростом n.
Абсолютная погрешность этого равенства
равна:
.
Точность этого равенства увеличивается
с ростом n.
Абсолютная погрешность этого равенства
равна:
 ,
где
,
где
 - остаток ряда. Таким образом, оценив
остаток можно найти ошибку. А для
знакочередующего ряда:
- остаток ряда. Таким образом, оценив
остаток можно найти ошибку. А для
знакочередующего ряда:
 .
. ;
; .
Этот ряд сходится по признаку Лейбница.
.
Этот ряд сходится по признаку Лейбница. :
:
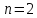 :
:
 ;
; :
:
 ;
; :
:
 ;-
этот в сумму не включается.
;-
этот в сумму не включается. .
На калькуляторе
.
На калькуляторе
 .
.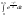 с точностью δ= 10-3.
с точностью δ= 10-3.
 -
не берущийся. Воспользуемся разложением
функции
-
не берущийся. Воспользуемся разложением
функции
 :
:
 .
Заменим x
на (
.
Заменим x
на ( ):
):




 :
:
 ;
; :
:
 ;
; :
:
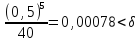 ;
- не включаем.
;
- не включаем. .
. .
. ,
где
,
где
 - коэффициенты ряда.
- коэффициенты ряда. - периодическая функция f(x)
на отрезке [-
- периодическая функция f(x)
на отрезке [- ]
удовлетворяет двум условиям:
]
удовлетворяет двум условиям: ,
т.е. равна среднему арифметическому
пределов функции f(x)
справа и слева;
,
т.е. равна среднему арифметическому
пределов функции f(x)
справа и слева; ,
,
 ,
сумма ряда равна:
,
сумма ряда равна:
 ;
;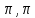 ]
имеет
место разложение:
]
имеет
место разложение:
 ,
коэффициенты вычисляются по формулам:
,
коэффициенты вычисляются по формулам:
 ;
;
 ;
;
 .
Это равенство может нарушится только
в точка разрыва функции и на концах
отрезка.
.
Это равенство может нарушится только
в точка разрыва функции и на концах
отрезка.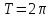 ,
на отрезке [
,
на отрезке [ ]
удовлетворяет теореме Дирихле, то для
вычисления коэффициентов
]
удовлетворяет теореме Дирихле, то для
вычисления коэффициентов
 ,
берутся интегралы в пределах [
,
берутся интегралы в пределах [ ];
]; периодическая функция является четной
и нечетной, то вычисление коэффициентов
Фурье упрощается, а сам ряд Фурье
становится неполным.
периодическая функция является четной
и нечетной, то вычисление коэффициентов
Фурье упрощается, а сам ряд Фурье
становится неполным.
 – четная;
– четная; – нечетная;
– нечетная; – нечетная;
– нечетная; –четная;
–четная; ;
;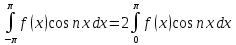 ;
;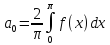 ;
;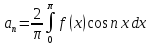 ;
; ;
; (1)
(1) ;
;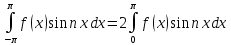 ;
; ;
; ;
; ;
; (2)
(2)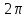 .
. ],
имеет период
],
имеет период

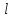 –
произвольное положительное число) и
удовлетворяет на этом отрезке условиям
Дирихле. Сделав подстановку
–
произвольное положительное число) и
удовлетворяет на этом отрезке условиям
Дирихле. Сделав подстановку ]
и имеет период
]
и имеет период
 .
Действительно, если
.
Действительно, если
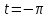 ,
то
,
то
 ,
если
,
если
 ,
то
,
то
 и при
и при
 имеем
имеем
 ;
;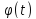 в ряд Фурье на отрезке [-
в ряд Фурье на отрезке [- ]
имеет вид:
]
имеет вид:
 ,
,
 ,
получим:
,
получим:
 .
. –периодических функций, остаются в
силе и для рядов Фурье функций, период
которых
–периодических функций, остаются в
силе и для рядов Фурье функций, период
которых
 .
В частности, если f(x)
на отрезке [
.
В частности, если f(x)
на отрезке [ ]
– четная,то ее ряд Фурье имеет вид:
]
– четная,то ее ряд Фурье имеет вид:
 .
.
 .
Теорема Абеля. Интервал и радиус
сходимости степенного ряда.
.
Теорема Абеля. Интервал и радиус
сходимости степенного ряда.
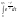 с точностью δ= 10-3.
с точностью δ= 10-3.