
metodichkaFTUG_chast2
.pdf
2) Так как при x 2
lim f x . Вычисляем:
x 2 0
lim |
x 2 3 |
|
lim |
x 2 0 |
x 2 2 |
|
x 2 0 |
lim |
x 2 3 |
|
lim |
x 2 0 |
x 2 2 |
|
x 2 0 |
функция не определена, рассмотрим lim f x и |
|||||||
|
|
|
|
|
|
x 2 0 |
|
2 0 2 3 |
|
lim |
4 0 3 |
|
64 |
; |
|
2 0 2 2 |
0 2 |
0 |
|||||
|
x 2 0 |
|
|
||||
2 0 2 3 |
|
lim |
4 0 3 |
|
64 |
. |
|
2 0 2 2 |
02 |
0 |
|||||
|
x 2 0 |
|
|
||||
Поэтому прямая x 2 является вертикальной |
асимптотой графика |
|
функции. |
|
|
Ищем горизонтальную асимптоту. Вычисляем lim |
x 2 3 |
, |
x x 2 2 |
|
|
это означает, что горизонтальных асимптот нет.
Выясним наличие наклонных асимптот. По формулам (6.36) и (6.37) находим:
|
|
|
|
|
|
|
|
x |
2 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
3 |
|
|
6x |
2 |
12x 8 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
k lim |
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
x x x 2 2 |
|
x |
|
x3 4x2 4x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
x3 |
|
|
6x2 |
|
12x |
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
1 |
6 |
|
12 |
|
8 |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
lim |
x3 |
|
|
|
|
x3 |
|
|
|
|
x3 |
|
|
x3 |
|
lim |
|
|
|
|
x |
|
x2 |
|
|
|
|
x3 |
1. |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
4 |
|
|
|
|
||||||||||||||||||||||||||||||
|
x |
|
|
|
|
x3 |
|
4x2 |
|
|
|
x |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
x2 |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
x3 |
|
x3 |
x3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
x 2 3 |
|
|
|
|
|
|
|
|
|
x3 6x2 12x 8 x3 4x2 4x |
|
|||||||||||||||||||||||||||||||||||||||||
b lim |
x 2 |
|
|
x |
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
4x 4 |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|||||||||||||||||||||||||||||||||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
10x2 8x 8 |
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
lim |
lim |
x |
x2 |
|
10. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
x2 4x 4 |
|
|
|
|
|
4 |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
x |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Приходим к выводу, что |
y x 10 – наклонная асимптота. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
Пример 2. Найти асимптоты графика функции: |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
1) |
y |
|
1 2x2 |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2) |
|
y |
|
x 1 |
|
. |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 1 |
|
|||||||||||||||||
|
x |
2 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Решение. |
|
|
1) |
|
|
|
Областью |
определения |
|
|
|
D(y) |
функции является то |
||||||||||||||||||||||||||||||||||||||||||||
140
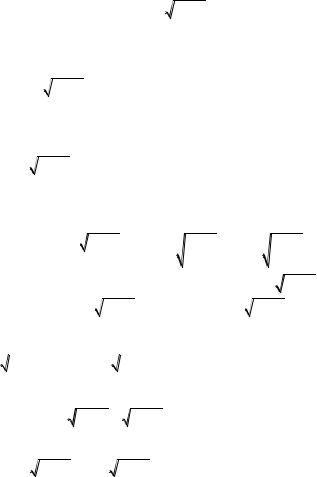
множество, на котором выполняется неравенство x2 4 0. Решив последнее неравенство, получим что D( y) ; 2 2; .
Определим вертикальные асимптоты графика функции. Рассмотрим поведение функции в окрестности точки x 2. Функция определена только в левой полуокрестности этой точки, поэтому вычисляем
левосторонний предел: lim f x lim |
1 2x2 |
|
|
|
||||||||||||||
|
7 |
. |
|
|||||||||||||||
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
x 2 0 |
x 2 0 |
|
x |
2 |
4 |
|
0 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
В окрестности точки |
x 2 функция определена только справа, поэтому |
|||||||||||||||||
в этой точке можем рассмотреть правосторонний предел: |
|
|||||||||||||||||
lim f x |
|
|
1 2x2 |
|
|
|
|
|
|
|
|
|
|
|
||||
lim |
|
|
|
7 |
. . |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
x 2 0 |
x 2 0 |
|
x |
2 |
4 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 2 и |
x 2 являются |
|||||
Приходим |
к |
заключению, |
что прямые |
|||||||||||||||
вертикальными асимптотами графика функции. Горизонтальных асимптот
нет, так как |
|
lim |
1 2x2 |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
x |
|
|
x |
2 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Найдем наклонные асимптоты: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
1 2x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|||||||||||||
|
|
|
|
|
|
|
f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
|
|||||||||||||||||||||||||
|
|
k lim |
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
x |
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
2. |
||||||||||||||||
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
x2 4 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
4 |
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
x |
|
|
|
x x |
|
|
|
|
|
|
x x |
1 |
|
|
|
x |
|
|
1 |
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
x |
2 |
|
|
|
|
|
|
|
x2 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
lim f |
x x |
|
|
|
|
|
|
1 2x2 |
|
|
|
|
|
|
|
|
|
1 2x2 2x x2 4 |
|
|||||||||||||||||||||||||||||||||||||
b |
lim |
|
|
|
|
|
|
|
|
|
|
2x |
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
x |
|
|
|
|
|
|
|
|
x |
|
|
x |
2 |
4 |
|
|
|
|
|
|
x |
|
|
|
|
x |
2 |
4 |
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
lim |
|
|
1 2x2 2 4x2 x2 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
1 2x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
x |
x2 4 |
2x |
|
x2 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
lim |
|
1 4x2 |
4x4 4x4 16x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
x 2x x2 |
2x2 x2 |
4 |
|
|
|
x2 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
lim |
|
|
|
|
|
|
12x2 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
x 2x3 2x2 |
|
|
x2 4 8x |
|
x2 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
Таким образом, |
|
|
y 2x – наклонная асимптота. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
2) Функция определена всюду на числовой прямой, кроме точки x 1,
141
т. е. D( y) ; 1 1; . |
Рассмотрим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
x 1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
x 1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
lim |
|
|
|
|
|
, |
lim |
|
|
|
|
|
|
. |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
x 1 |
0 |
|
|
|
||||||||||||||||||||||||||||||||
x 1 0 x 1 |
|
|
|
|
|
|
|
x 1 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
Прямая x 1 – вертикальная асимптота. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
Найдем горизонтальные асимптоты: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
lim |
|
x 1 |
|
|
lim |
|
x 1 |
1, |
|
|
|
|
|
|
|
|
|
|
lim |
|
|
x 1 |
|
|
|
lim |
x 1 |
1. |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
x x 1 |
|
|
|
|
x x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
x 1 |
x x 1 |
||||||||||||||||||||||||
x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Получаем, что прямая |
y 1 является горизонтальной асимптотой при |
||||||||||||||||||||||||||||||||||||||||||||||
x x 1 , |
а |
|
прямая |
y 1 |
– |
горизонтальная асимптота при |
|||||||||||||||||||||||||||||||||||||||||
x x 1 . Ищем наклонные асимптоты: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
f x |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
k lim |
|
|
|
|
lim |
|
x 1 |
|
|
lim |
|
x2 |
|
|
|
x |
|
|
|
x2 |
|
|
|
0 |
0. |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
1 |
x |
|
|
|
x |
|
x |
x |
x |
|
x |
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Наклонных асимптот нет.
План исследования функции и построения графика
1.Найти область определения D(f) функции f(x).
2.Исследовать функцию на четность.
3.Исследовать функцию на периодичность.
4.Найти промежутки знакопостоянства функции.
5.Исследовать функцию на непрерывность, дать классификацию точек разрывов.
6.Найти асимптоты графика функции (горизонтальную, вертикальную, наклонную).
7.Исследовать функцию на монотонность. Найти точки экстремума функции.
8.Исследовать график функции на выпуклость, вогнутость. Найти точки перегиба.
9.При необходимости найти точки пересечения с осью Ox (нули функции) и точки пересечения с осью Oy.
10.Построить график функции, используя результаты исследования.
Пример 3. Исследовать функцию y x 1 2 x 3 и построить ее график.
142

Решение. Исследование функции произведем согласно указанному выше плану.
1. Область определения функции: D f ; .
2. Исследуем функцию на четность и нечетность:
y x x 1 2 x 3 y x . Функция не является четной и нечетной.
3. Функция непериодическая.
4. Найдем промежутки знакопостоянства функции с помощью метода интервалов (рис. 6.10).
|
|
+ |
|
+ |
– |
– 3 |
1 |
x |
|
|
|
Рис. 6.10 |
|
|
Получаем: |
f x 0, |
если x ; |
3 ; |
|
|
f x 0, |
если x 3; |
1 1; |
. |
5. Функция непрерывна на всей числовой оси.
6. Горизонтальных асимптот функция не имеет, так как она определена на всей числовой прямой.
Ищем наклонную асимптоту y kx b. |
k lim |
x 1 2 x 3 |
. |
||||||||||||||||
|
x |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
Функция наклонных асимптот также не имеет. |
|
|
|
||||||||||||||||
7. Исследуем функцию на монотонность и экстремум. Найдем y x : |
|||||||||||||||||||
y x 1 2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
3 |
2 x |
1 x 3 |
x 1 2 |
|
|
|
|||||||||||||
|
|
x 1 |
2 |
|
x 3 |
|
x 1 |
|
x 1 |
3x 5 |
|
. |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Производная существует |
x ; |
|
. Критическими точками |
||||||||||||||||
являются те, для которых |
y x 0, |
т. е. x1 |
|
5 |
и x2 1. |
|
|||||||||||||
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
||
Исследуем |
знак производной |
|
для |
|
конкретных |
промежутков, на |
|||||||||||||
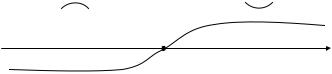
которые критические точки делят числовую ось (рис. 6.11).
у |
|
|
|
|
|
у |
+ |
|
|
|
+ |
|
|
5 |
– |
1 |
х |
|
3 |
|
|
|
143
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 6.11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Согласно |
|
теореме |
|
|
1, |
|
|
функция |
|
|
|
|
возрастает |
на |
множестве |
|||||||||||||||||||||||||||||||||||||
|
|
|
5 |
|
1; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
; |
|
|
|
|
|
|
|
и убывает на |
|
|
|
|
; 1 , |
что схематически показано на |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
рис. 17.8. Согласно |
|
|
теореме |
3, |
|
|
в |
|
точке |
x |
5 |
|
она имеет локальный |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
3 |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
максимум, а в точке х = 1 – минимум. Найдем их значения: |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
5 |
|
|
2 |
|
|
|
5 |
|
|
|
|
|
|
|
64 |
|
4 |
|
256 |
|
|
|
|
|
|
||||||||||
ymax |
y |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
9,5; |
|
||||||||||||||||||||||
3 |
3 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 3 27 |
|
|
|
|
|
|
|||||||||||||||||
ymin |
y 1 1 1 2 1 3 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
8. Исследуем график функции на выпуклость, вогнутость и перегиб. |
||||||||||||||||||||||||||||||||||||||||||||||||||||
Вычислим производную 2-го порядка: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
y |
|
x |
|
|
|
|
x 1 |
|
3x 5 |
|
3x 5 3 |
|
x 1 6x 2. |
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
x 0, |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Если |
|
y |
|
то x 3 , |
т. е. x 3 |
– критическая точка 2-го рода, |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
иных нет. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Имеем y x 0, |
если x |
|
; |
|
1 |
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
y x 0, |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
если |
x |
|
|
|
; |
|
(рис. 6.12). |
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
у |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
у |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х |
||||
|
|
|
|
|
|
|
|
|
|
|
|
– |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 6.12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Значит, график функции является выпуклым на |
|
; |
|
1 |
|
и вогнутым |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
на |
|
; |
|
, |
(согласно теореме 7), |
x |
|
|
|
|
– точка перегиба (теорема 8). |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
9. Найдем точки пересечения графика с координатными осями.
Если у = 0, т. е. x 1 2 x 3 0, то х = 1, х = –3 – точки пересечения с осью Ох (нули функции).
144

Если х = 0, то у = 3 – точка пересечения с осью Оу.
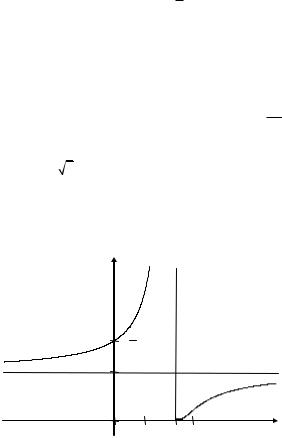
10. Используя полученные данные, построим график функции (рис.
6.13).
у10
9
3
–3 |
|
5 |
|
1 |
1 |
х |
|
3 |
|
|
|||
|
3 |
|
|
|||
|
|
|
|
|
Рис. 6.13 |
|
Заметим, что E f ; .
1
Пример 4. Исследовать функцию y e 2 x и построить ее график. Решение. 1. Область определения: D f ; 2 2; .
2.Поскольку область определения D(f) функции не является множеством, симметричным относительно х = 0, то функция не является четной и нечетной.
3.Функция непериодическая.
|
|
1 |
|
4. Для всех x D f |
выполняется e2 x |
0, т. е. функция |
|
положительна на всей области определения.
5. Функция непрерывна на своей области определения, х = 2 – точка разрыва.
Исследуем характер разрыва.
Вычисляем односторонние пределы в точке х = 2:
|
1 |
|
|
1 |
|
lim e2 x , |
lim e2 x 0. |
||||
x 2 0 |
x 2 0 |
||||
Следовательно, х = 2 – точка разрыва 2-го рода (бесконечный скачок).
145
6. Найдем асимптоты функции. Поскольку
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
lim e2 x e0 |
1, |
lim e2 x e0 |
1, то у = 1 – горизонтальная асимптота. |
|||||||||||||
x |
|
|
|
x |
|
|
|
|
|
|
|
|
||||
Мы показали, что в точке х = 2 имеется бесконечный скачок, а поэтому |
||||||||||||||||
х = 2 – вертикальная асимптота. |
|
|
|
|
|
|
|
|
||||||||
Ищем наклонную асимптоту y kx b : |
|
|
|
|
|
|
||||||||||
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
e2 x |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
k lim |
|
|
|
0, |
b lim e2 x kx |
|
lim e2 x 1. |
|||||||||
|
x |
|||||||||||||||
|
x |
|
|
|
|
x |
|
|
|
x |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Получаем у = 1 – это горизонтальная асимптота. Наклонных асимптот нет.
7. Исследуем функцию |
на |
монотонность и |
|
экстремум. Найдем |
||||||||||
|
|
|
|
|
|
1 1 |
|
1 |
|
|
|
|||
|
1 |
1 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
e2 x |
|
|
||||
|
|
|
|
|
|
|
||||||||
производную функции: y e2 x |
e2 x |
|
|
|
|
|
|
|
|
. |
||||
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
2 x |
2 |
|
|
2 x |
2 |
|
||
|
|
|
|
|
|
|
|
|
||||||
Производная положительна на всей D(f). Следовательно, функция возрастает всюду, где она определена. Экстремума нет.
8. Находим вторую производную:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 x |
2 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
2 x |
e |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
2 x |
|
2 x |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
e2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 x |
4 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
e |
2 x |
2 x 2 |
e |
2 x |
2 2 x 1 |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
2 x 2 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 x 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
e2 x |
2 2 x e |
2 x |
|
|
|
e |
2 x |
1 4 2x |
|
|
e |
2 x |
5 2x |
. |
|||||||||||||||||||||||||||
|
|
|
|
|
|
2 x 4 |
|
|
|
|
|
|
|
2 x 4 |
|
|
|
|
|
|
2 x 4 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Поскольку |
e2 x |
0 и |
2 x 4 |
0 |
на D(f), |
то знак производной 2-го |
|||||||||||||||||||||||||||||||||||||
порядка зависит от знака выражения 5 – 2х. Очевидно, что y x 0, если
|
|
|
5 |
|
x ; |
2 |
2; |
|
. На этих промежутках график функции вогнут. |
|
||||
|
|
|
2 |
|
146
|
5 |
|
|
|
y x 0, т. е. график функции является |
|
Если |
x |
|
; |
, |
то |
|
|
||||||
|
|
2 |
|
|
|
|
выпуклым на этом промежутке. Точка x 52 является точкой перегиба, так
как при этом значении вогнутость графика изменяется на его выпуклость. Найдем ординату, соответствующую точке перегиба:
|
|
|
|
1 |
|
|
|
|
|
5 |
|
|
2 |
5 |
|
|
|
e |
2 |
e 2 |
0,14. |
|||||
y |
|
|
|
|||||
|
|
|||||||
|
2 |
|
|
|
|
|
|
1
9. График функции не пересекает ось Ох, так как e2 x 0 для всех x D f .
Если х = 0, то y 
 e – точка пересечения с осью Оу.
e – точка пересечения с осью Оу.
10. Используя результаты исследования, строим график функции (рис.
6.14).
у
2

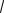 e
e
1
0 |
1 |
2 |
5 |
x |
|
||||
|
|
|
2 |
|
Рис. 6.14
В дополнении отметим, что E f 0; 1 1: .
Пример 7. Для перевозки груза необходимо изготовить контейнер с крышкой, объем которого равен 72 м3, а стороны основания относятся как 1:2. Определить, каковы должны быть размеры контейнера, чтобы на его
147
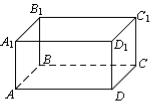
изготовление ушло наименьшее количество материала.
Решение. Контейнер представляет собой прямоугольный параллелепипед ABCDA1B1C1D1, объем которого 72 м3 (рис. 6.15).
Рис. 6.15
Пусть k – коэффициент пропорциональности. Тогда стороны основания равны: AB k, AD 2k.
V AB AD AA , |
|
AA |
V |
, т. е. AA |
72 |
|
36 |
. |
1 |
|
1 |
AB AD |
1 |
2k2 |
|
k2 |
|
|
|
|
|
|
||||
Количество материала, необходимого на изготовление контейнера,
численно |
равно полной поверхности |
параллелепипеда, т. е. |
|||
S Sбок 2Sосн . |
|
|
|||
Выразим площадь боковой поверхности: |
|
|
|||
Sбок |
2 AB AD AA1 2 k 2k |
36 |
|
216 |
. |
|
|
||||
|
|
k2 |
k |
||
Площадь основания: Sосн AB AD k 2k 2k 2 .
Поэтому площадь полной поверхности выражается функцией
S |
216 |
4k 2 |
|
216 4k3 |
. |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
k |
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Исследуем полученную функцию на экстремум с помощью первой |
|||||||||||||||||||||
производной: |
|
|
|
|
|
|
k 216 |
|
|
|
|
|
|
|
|
||||||
|
216 4k |
3 |
|
|
12k |
2 |
4k |
3 |
8k |
3 |
216 |
|
|||||||||
|
|
|
|
|
|
|
|||||||||||||||
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|||||||
|
|
k |
|
|
|
|
|
|
k |
|
|
|
|
|
|
k |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Критические точки: значение k = 0 (производная не существует) – не подходит по смыслу задачи.
S 0, т. е. 8k3 216 0, k3 |
27, |
k 3. |
|
При переходе через точку |
|
k 3 |
производная функции меняет свой |
знак с «–» на «+». Значит, при |
k 3 площадь полной поверхности будет |
||
наименьшей. Получаем размеры контейнера:
148

AB 3; AD 2 3 6; AA1 36 4 . 32
Задания для решения в аудитории
I уровень
1.1. Определите, сколько вертикальных асимптот имеет график функции y f x :
|
1 |
|
|
|
ln x 1 |
|
|
|
|
|
|
sin x |
|
|
|
|
x 4 |
|||||||||
1) |
y |
|
|
; 2) y |
|
|
|
; 3) |
|
y |
|
|
|
; 4) |
y |
|
|
|
|
. |
||||||
x 3 x 5 |
x 2 |
x2 6x 9 |
|
x 1 |
2 |
|||||||||||||||||||||
|
1.2. Найдите асимптоты кривых: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
2x 1 |
|
|
x2 4x 3 |
|
|
|
|
x 3 |
|
|
|
|
|||||||||||||
1) y |
; 2) |
y |
; 3) |
y |
|
|
|
; 4) y 1 3 2x x2 . |
||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
x 1 |
|
|
x 1 |
|
|
|
x |
3 |
1 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
II уровень
2.1. Среди данных функций выберите те, которые имеют вертикальные асимптоты (ответ подтвердите доказательством):
1)y x2 5x 6 ;
x1
2)y x2 2x ;
x2 4
|
|
|
|
|
|
|
|
||
|
x 1, |
если x 1, |
|||||||
|
|
||||||||
|
|
|
|
|
|
|
|||
3) |
y |
1 |
|
, |
|
если x 1. |
|||
|
|
|
|
|
|
||||
|
|
|
|
|
|||||
|
1 |
x |
|
||||||
|
2x2 |
7, |
если x 2, |
||||||
|
|
|
|
|
|
|
|
||
4) |
y |
1 |
|
|
, |
|
если x 2. |
||
|
|
|
|
|
|
||||
|
|
|
|
|
|||||
|
x |
2 |
|
|
|
||||
2.2. Найдите асимптоты кривых:
|
|
|
x3 x2 x 2 |
|
1 |
; 3) y x3 e x 1 ; 4) y ln 4 x2 ; |
||||||||||||||||||||||||||||||||
1) |
y |
|
; 2) y x e |
|
x2 |
|||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
3x2 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
5) |
y |
x |
; |
|
6) y |
arctg x x : |
7) |
y |
|
|
x 2 |
|
|
; |
8) |
y ln |
1 x |
|
. |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
x 1 |
|||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
ln x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
1 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
2.3. Исследуйте функцию и постройте ее график: |
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
8 x3 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||||||||||||||
1) |
y |
|
|
|
|
; 2) y |
; 3) |
y |
4х2 |
; 4) |
y 3 1 x3 ; |
|
||||||||||||||||||||||||||
|
|
|
x2 4х 3 |
|
|
х2 |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
y |
(x 1) |
3 |
|
|
|
y |
|
x |
|
y |
2x |
|
|
|
|
|
|
y |
|
ex |
|
|
|
|
|||||||||||||
5) |
|
|
; 6) |
|
; 7) |
|
|
; |
|
|
8) |
|
|
. |
|
|
|
|
||||||||||||||||||||
3x2 |
|
1 x2 2 |
ex |
|
|
|
|
x |
|
|
|
|
||||||||||||||||||||||||||
149
