1-41

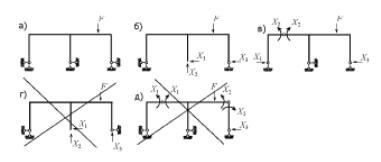
35. Сущность метода сил. Основная система и основные неизвестные.

В статически неопределимой системе удаляются лишние связи, а вместо них прикладываются неизвестные силы. Полученную т.о. систему наз. основной системой метода сил, а неизвестные силы - основными неизвестными этого метода. Сопоставляя перемещения заданной и основной систем, получают уравнения для определения основных неизвестных. Основная система д.б. геометрически неизменяемой и неподвижной. Для любой статически неопределимой рамы можно выбрать несколько основных систем.

Пример: Степень статической неопределимости рамы, изображенной на рис. 8.11,а, равна трем. Возможные варианты основных систем показаны на рис. 8.11,б- в. На рис. 8.11,б показано, что за основные неизвестные метода сил приняты усилия в опорных связях заданной рамы, а по рис. 8.11,в основными неизвестными

являются X1, X3 - реакции в опорных связях и X2 - силы взаимодействия между примыкающими к шарниру стержнями. Системы, показанные на рис. 8.11,г,д, не м.б. выбраны в качестве основных, так как являются мгновенно изменяемыми.

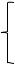
36. Канонические уравнения метода сил. Вычисление коэффициентов и свободных членов. Проверки вычислений.

δ11X1+δ12X2+δ13X3+…+δ1nXn+∆1F=0

δ21X1+δ22X2+δ23X3+…+δ2nXn+∆2F=0

δn1X1+δn2X2+δn3X3+…+δnnXn+∆nF=0

Эти уравнения наз. каноническими уравнениями метода сил для расчета системы на действие внешней нагрузки. Суть i -го уравнения сводится к тому, что перемещение точки приложения неизвестной Xi по ее направлению, вызываемое всеми неизвестными и внешней нагрузкой, равно нулю. Решение системы канонических уравнений позволяет найти значения основных неизвестных.

Коэффициенты и свободные члены уравнений вычисляются по правилам определения перемещений. Для рамных систем, испытывающих преимущественно изгибные деформации, ограничиваются учетом влияния на перемещения только изгибающих моментов. Поэтому δik и ∆iF вычисляются по формулам: δik=∑∫(M̅iM̅kdx)/EJ; ∆iF=∑∫(M̅iMFdx)/EJ, где M̅i, M̅k – изгибающие моменты, вызываемые безразмерными силами соответственно Xi=1 и Xk=1; MF – изгибающий момент, вызываемый внешней нагрузкой.

Значения коэффициентов и свободных членов уравнений получаются более точными, если при их определении учитываются, кроме изгибающих моментов, продольные и попе­ речные силы в элементах рамы.

Значения коэффициентов и свободных членов уравнений получаются более точными, если при их определении учитываются, кроме изгибающих моментов, продольные и попе речные силы в элементах рамы.

Проверка правильности опр-ия коэф-тов и свободных членов канонических ур-ий. Решив систему ур-ий, получим неизвестные Х1,Х2,…,Хn. Рез-ты расчета зависят от того, насколько точно опр-ны коэф-ты этих ур-ий. Большое значение имеет контроль правильности опр-ия коэф-тов: для системы с n лишними связями ординаты эпюры моментов Ms в осн. системе от действия всех единичных сил Х1, Х2, …, Хn, заменяющих действие лишних связей, = сумме ординат соотв-щих единичных эпюр М1, М2, …, Мn в том же сечении: Ms=М1+М2+…+Мn. Найдем сумму коэф-тов при неизвестных 1го ур-ия системы: δ1s =δ11+δ12δ+δ13+…+δ1n или δ1s= Σ∫(М1Мs/EI)ds, от 0 до s. Т.о. рез-т перемножения единичной эпюры М1 и суммарной единичной эпюры Мs д.б. = алгебраической сумме ко- эф-тов при неизвестных 1го канонического ур-ия. Сумма коэф-тов при неизвестных 2го канонического ур-ия: δ2s =δ21+δ22δ+δ23+…+δ2n= Σ∫(М2Мs/EI)ds от 0 до s.

Аналогичные равенства можно записать для остальных канонический ур-ий. Такие проверки наз. построчными. Если система не высокого порядка, обычно пользуются универсальной проверкой, при к-ой рез-т умножения суммарной единичной эпюры саму на себя д.б. = алгебраической сумме коэф-тов при неизвестных всех ур-ий системы:

Σ∫(М2s/EI)ds= Σδik (i,k=1,2,3,…,n). однако при большом числе коэф-тов после установления путем универсальной проверки еще выполнить доп-ую работу для выявления того, какой из коэф-тов содержит эту ошибку, т.е. делать построчные проверки. Проверка свободных членов канонических ур-ий производится также с использ. суммарной единичной эпюры Ms. Алгебраическая сумма свободных членов д.б. = рез-ту, полученному перемножением эпюры Ms на эпюру моментов от заданной нагрузки в основной системе:

Σ∆ip=Σ∫(МsМp/EI)ds (i=1, i=n; от 0 до s).

37. Использование симметрии при расчётах рам методом сил. Групповые неизвестные.

Основную систему для рамы, имеющей симметричное распределение линейных размеров и жесткостей стержней, следует принимать симметричной. От действия на раму симметричной нагрузки распределение усилий в ее элементах окажется симметричным, и наоборот: кососимметричная нагрузка вызывает кососимметричные усилия. Поэтому эпюры изгибающих моментов в основной системе будут либо симметричными, либо кососимметричными. Симметричные и кососимметричные эпюры являются

взаимно ортогональными.

Пример: Приняв для рамы, показанной на рис. 8.15,а, основную систему, изображенную на рис.

8.15,б, получим симметричные эпюры M̅1, M̅2, M̅4 (рис. 8.15,в,г,е) и кососимметричную

M̅3 (рис. 8.15,д). Следовательно, коэффициенты δ13, δ31, δ23, δ32, δ34, δ43 равны нулю. Вычеркнув в системе уравнений слагаемые, включающие перечисленные коэффициенты,

увидим, что она распалась на подсистему, содержащую только симметричные неизвестные и уравнение с кососимметричной неизвестной.

Групповые неизвестные.

Во многих случаях основные неизвестные невозможно расположить на оси симметрии. Так, для рамы, изображенной на (рис. а), число лишних связей равно шести. Симметричная основная система м.б. принята по варианту, показанному на (рис. б). Однако в этом случае при загружении ее силами Xi=1 ни одна из эпюр изгибающих моментов не получится симметричной или кососимметричной, а значит, все побочные коэффициенты δik будут отличными от нуля. Чтобы получить симметричные и кососимметричные эпюры усилий необходимо вместо традиционных неизвестных Xi

ввести новые (будем обозначать их Zi), п. c. группы сил.

На (рис. в) показана та же основная система с новыми неизвестными. Сопоставляя расположение неизвестных на (рис. б,в), находим правила преобразования их: каждой паре симметрично расположенных неизвестных Xi соответствует операция сложения или вычитания симметричных и кососимметричных групповых неизвестных Zi.

В частности, X1=Z1+Z2, X4=Z1-Z2, откуда следуют и выражения для Z: Z1=(X1+X4)/2, Z2=(X1-X4)/2.

Эпюры усилий от групповых неизвестных показаны на (рис. г-и). Вследствие взаимной ортогональности симметричных и кососимметричных эпюр система канонических уравнений распадается на две независимые: в одну из них войдут только симметричные неизвестные Z1, Z3, Z5, а в другую - кососимметричные (Z2, Z4, Z6).

38. Особенности определения перемещений в статически неопределимых системах.

1 способ. Для определения перемещений с помощью формулы Мора необходимо, построить эпюры изгибающих моментов для заданного нагружения системы и для вспомогательного. Тогда искомое перемещение будет вычисляться по формуле: ∆kF=∑∫(M̅kMdx)/EJ.

Однако такой способ вычисления не совсем удобен, так как потребуется дважды рассчитать статически неопределимую систему.

2 способ. Если загрузить основную систему заданной нагрузкой и основными неизвестными, которые определены из канонических уравнений, то эпюра момен-

тов в этой статически определимой системе (рис. в) будет полностью совпадать с окончательной эпюрой моментов (рис. а). Следовательно, рассматривая состояние рамы на (рис. в) как исходное, можно для определения перемещения точки k во вспомогательном состоянии принимать статически определимую систему (рис. г). В этом случае: ∆kF=∑∫(M̅0kMdx)/EJ, где M̅0k – изгибающие моменты в статически определимой системе, возникающие от Fk=1.

При определении перемещений в статически неопределимых системах можно одну из “перемножаемых” эпюр строить в заданной статически неопределимой системе, а вторую - в любой статически определимой, полученной из заданной системы.

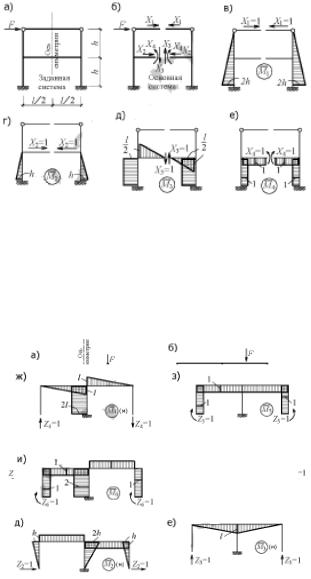
Пример: (рис. а) показана эпюра изгибающих моментов в статически неопределимой раме от заданной нагрузки, а на (рис. б) - эпюра моментов в той же раме от Fk - 1. По формуле полу-

чим: ∆kF=∑∫(M̅kMdx)/EJ=(l/24EJ)[-2(15lql2/176*22)- 2(13lql2/176*44)+(15lql2/176*44)+(13lql2/176*22)]+ (l/24EJ)[2(3lql2/176*11)-2(13lql2/176*44)-(13lql2/176* 11)+(3lql2/176*44)]+(l/6EJ)[(3lql2/176*11)-4(3l7ql2/

352*88)]= -(ql4/1408EJ) м.

На (рис. в) показана эпюра моментов в статически определимой раме от Fk -1, а на (рис. г) - эпюра мо-

ментов в основной системе от заданной нагрузки. По формуле получим: ∆kF=∑∫(M̅0kMdx)/EJ=(l/24EJ)[-2(lql2/4*22)+2(lql2/4*44)]= -(ql4/1408EJ) м. 3 способ: ∑∫(M̅kM0Fdx)/EJ= -(ql4/1408EJ) м.

39. Расчёт статически неопределимых ферм.

Расчет статически неопределимых ферм, производится методом сил. Основная система метода сил выбирается путем разрезания стержней фермы, либо путем удаления опорных связей (рис. 12.2), которые не являются абсолютно необходимыми.

Канонические уравнения метода сил имеют стандартный вид:

При узловой нагрузке в стержнях статически неопределимых ферм, как и других шарнир- но-стержневых систем, будут возникать только продольные силы. Следовательно, перемещения в фермах будут зависеть только от продольных деформаций их стержней, и для вычисления перемещений следует использовать формулу Максвелла: δik=∑(NiNks)/EA; ∆iF=∑(NiNFs)/EA (i,k = 1 ,2 ,...,n), где знак суммирования ∑ распространяется на все стержни фермы; Ni, Nk, NF — соответственно усилия в стержнях основной системы метода сил от единичных значений основных неизвестных(Xi =1, Xk=1) и от заданной нагрузки

F;

s и EA - длина и жесткость на растяжение-сжатие соответствующего стержня фермы. Окончательные усилия в стержнях статически неопределимых ферм вычисляют по фор-

муле: N=NF+(от i=1 до n)∑NiXi.

Расчет ферм методом перемещений приводит к значительно большему количеству основных неизвестных. В плоских фермах каждый узел за счет продольных деформаций стержней обладает двумя линейными смещениями. Количество основных неизвестных метода перемещений для ферм независимо от их статической определимости или неопредилимости вычисляется по формуле: n=2У-C0.

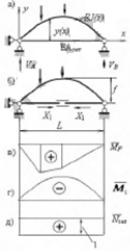
40. Расчёт двухшарнирных арок.

Двухшарнирная арка с затяжкой является внешне безраспорной. Распор воспринят затяжкой, и его следует рассматривать как внутреннюю растягивающую силу в затяжке. Двухшарнирная арка с затяжкой является один раз статически неопределимой, и ее можно рассчитать методом сил.

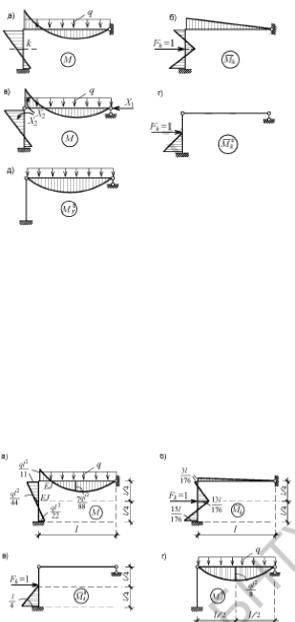
Рассмотрим двухшарнирную арку с прямолинейной затяжкой, расположенной в уровне опор (рис. а). Арка имеет переменное по длине пролета поперечное сечение и загружена вертикальной нагрузкой. Основную систему метода сил можно получить, рассекая затяжку (удаляя из затяжки связь, воспринимающую продольную силу). Основным неизвестным метода сил будет усилие в затяжке Nзат=X1 (рис. б).

Каноническое уравнение метода сил имеет вид: δ11X1+∆1F=0, где δ11 - взаимное перемещение концов затяжки в месте разреза, вызываемое единичным усилием в затяжке X1=1; ∆1F - взаимное перемещение концов разрезанной затяжки от нагрузки. При разрезанной затяжке основная система арки п.c. криволинейную балку. Нагрузка, приложенная к арке, вызывает изгибающие моменты только в арке как в криволинейной балке M̅F=M0x (рис. в). Усилий в разрезанной затяжке нагрузка не вызывает.

Единичное неизвестное вызывает изгибающие моменты в арке M̅1=-y(х). Единичная эпюра изгибающих моментов повторяет очертание оси арки (рис. г). В затяжке единичное неизвестное вызывает постоянную растягивающую продольную силу N̅зат=1(рис. д).

Расчета арок состоит в том, что интегралы Мора для вычисления перемещений в арках должны браться по длине оси арки, т.е. являются криволинейными интегралами. Грузовое перемещение находят по ф-ле Мора: ∆1F=(по S)∫(M̅1MFds)/EJ(x)=-(по S)∫(y(x)MFds)/EJ(x).

Коэф-т при единичное перемещение, вычисляют с учетом продольных деф-ций затяжки,

находят по ф-ле: δ11=(по S)∫((M̅12ds)/EJ(x))+(N̅зат2L)/EAзат=(по S)∫([y(x)]2ds/EJ(x))+ L/EAзат.

Чтобы в этих криволинейных интегралах перейти к интегрированию по длине пролета, т.е. по абсциссе х, введем замену: ds=dx/cosφ(x), где φ(x) - угол наклона к горизонтали касательной к оси арки в сечении с абсциссой x.

В рез-те для вычисления коэф-та и свободного члена канонического уравнения метода сил получим:

δ11=(от 0 до L)∫([y(x)]2dx/EJ(x)cosφ(x))+L/EAзат, ∆1F=-(от 0 до L)∫(y(x)MFdx)/EJ(x)cosφ(x).

Внутренние силы в любом сечении двухшарнирной арки можно найти по формулам:

Mx=Mx0-X1yx; Qx=Qx0cosφx-X1sinφx; Nx=-(Qx0sinφx+X1cosφx).

41. Расчёт бесшарнирных арок

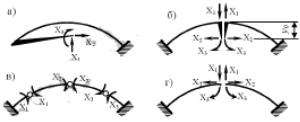
Бесшарнирная арка является трижды статически неопределимой. Для определения трех основных неизвестных метода сил необходимо составить и решить три канонических уравнения. Соответствующим выбором основной системы метода сил можно добиться даже полного разделения системы канонических уравнений на три отдельных уравнения, каждое с одним неизвестным, при произвольном очертании оси арки и произвольной нагрузке. Варианты основных систем, представленные на рис. 13.5,а,б,в, позволяют обнулить побочные коэффициенты канонических уравнений и привести уравнения к виду:

δ11X1+∆1F=0; δ22X2+∆2F=0; δ33X3+∆3F=0.

Добиться такого результата можно ценою дополнительных вычислений по определению длины жестких консолей (рис. а). Например, в симметричной арке (рис. б) основное неизвестное X1 является кососимметричным и отделено от двух других прямосимметричных неизвестных. Разделить

основные неизвестные X2 и X3 можно, подобрав длину абсолютно жестких консолей y0 так, чтобы перемещение δ23 равнялось нулю.

Основная система, полученная сквозным разрезом бесшарнирной арки по оси симметрии (рис. г), позволяет сразу разделить три совместных канонических уравнения на одно неза-

висимое уравнение: δ11X1+∆1F=0; δ22X2+δ23X3+∆2F=0; δ32X2+δ33X3+∆3F=0.