Готовимся к экзамену по математике_Крамор В.С_2008 -544с

В. С.Крамор

Готовимся к экзамену

по МАТЕМАТИКЕ

Учебное пособие

Москва

ОНИКС Мир и Образование

ПРЕДИСЛОВИЕ

À

Данная ни а предназначена для самостоятельно о повторения ш ольно о урса ал ебры и начал анализа, а та же для под отов и выпус ным э заменам в средней ш оле и вступительным э заменам в высшее учебное заведение.

Весь учебный материал разбит на 22 темы, оторые имеют одну и ту же стру туру. Каждая тема содержит: теоретичес ие сведения; онтрольные вопросы; упражнения (в лючая задания для повторения); ответы, решения и методичес ие у азания упражнениям.

Вразделе «Теоретичес ие сведения» приводятся формулиров и правил, определений, теорем и т. д. Весь учебный материал изложен онспе тивно в той же последовательности, что

ипри изучении е о в ш оле. В этом разделе имеются та же подробно разобранные примеры, позволяющие частично за репить усвоение теории. У азанный раздел является узловым, пос оль у в случае затруднений при ответах на онтрольные вопросы или при решении упражнений учащийся может получить необходимые онсультации, обращаясь справочному материалу.

Раздел «Контрольные вопросы» призван обеспечить онтроль за усвоением теоретичес о о материала. Отвечая на поставленные вопросы, учащийся сможет за репить полученные им теоретичес ие знания.

Вразделе «Упражнения» содержатся разнообразные примеры и задачи, относящиеся данной теме. Ко всем упражнениям даны ответы. Значительная часть упражнений сопровождается подробными решениями и методичес ими у азаниями. Каждый этап решения в лючает необходимую информацию о правомерности то о или ино о ша а. Среди упражнений имеются примеры и задачи довольно высо о о уровня сложности, взятые из вариантов, предла авшихся на вступительных э заменах в различные вузы. Наличие именно та их упражнений

3

позволяет приобрести необходимые умения и навы и, усвоить мно очисленные стандартные и нестандартные приемы решения математичес их задач.

Начиная с темы 3 раздел «Упражнения» содержит та же задания для повторения. Эти задания в лючают не толь о примеры и задачи та о о же типа, что и в предыдущих темах, но и упражнения, оторые по тем или иным причинам в предыдущие темы не вошли. Кроме то о, здесь приводится большоеоличество те стовых задач, решение оторых, а по азывает пра ти а, вызывает у учащихся определенные трудности. Подробные решения та их задач, приведенные в ни е, позволяют учащемуся устранить имеющиеся у не о пробелы.

Кни а завершается разделом «Приложение», оторый содержит 30 вариантов билетов, предла авшихся на вступительных письменных э заменах по математи е ( 20 вариантам даны ответы) в различных вузах страны. Самостоятельное решение та их задач поможет о ончательно за репить знания

иумения, приобретенные в процессе изучения данной ни и,

иа можно лучше под отовиться выпус ным и вступительным э заменам по математи е.

Успехов вам, настоящие и будущие абитуриенты!

Автор

4

Т е м а 1

À

Натуральные числа и действия над ними. Сложение и законы сложения. Вычитание. Умножение и законы умножения. Деление.

Признаки делимости чисел. Понятие множества. Операции над множествами.

Взаимно однозначное соответствие.

Простые и составные числа. Наибольший общий делитель. Наименьшее общее кратное

Теоретичес ие сведения

1. Натуральные числа и действия над ними

1°. Понятие натурально о числа относится простейшим, первоначальным понятиям математи и и не подлежит определению через дру ие, более простые понятия.

2°. Натуральные числа получаются в результате счета предметов, например 1, 3, 100 и т. д.

3°. Та им образом, натуральные числа в поряд е возрастания можно написать а ряд чисел 1, 2, 3, 4, ... .

4°. Для натуральных чисел определены следующие действия: сложение, вычитание, умножение, деление, возведение в степень и извлечение орня.

Заметим, что сложение и умножение выполнимы все да, т. е. в результате этих действий получаются та же натуральные числа.

2. Сложение и законы сложения

1°. Результат сложения двух или нес оль их чисел называют их с ммой, а сами числа — сла аемыми.

Например, a + b + c + ... + k = P. Здесь P — сумма; a, b, c, ..., k — сла аемые.

2°. Для любых натуральных чисел a и b верно равенство a + b = b + a. Это свойство называют переместительным ( ом-

5

мутативным) за оном сложения, оторый формулируется та : от перестанов и сла аемых значение суммы не изменится.

3°. Для любых натуральных чисел a, b и c верно равенство a + b + c = (a + b) + c = a + (b + c). Это свойство называют сочетательным (ассоциативным) за оном сложения, оторый формулируется та : значение суммы не изменится, если а уюлибо руппу сла аемых заменить их суммой.

3. Вычитание

1°. Вычесть из числа a число b — значит найти та ое число x,оторое в сумме с числом b дает a, т. е. b + x = a.

2°. Число x называют разностью чисел a и b и обозначают a – b; число a называют меньшаемым, число b — вычитаемым.

3°. Для натуральных чисел вычитание не все да выполнимо. Например, 4 – 4; 2 – 7; 17 – 30, т. е. в результате мы не получим натуральное число.

4. Умножение и законы умножения

1°. Умножить число a на число b — значит найти сумму b сла аемых, аждое из оторых равно a. Выражение ab называют произведением, а числа a и b — множителями.

Например, a · 3 = a + a + a; b · 5 = b + b + b + b + b.

2°. Для любых натуральных чисел a и b верно равенство ab = ba. Это свойство называют переместительным за оном умножения, оторый формулируется та : от перестанов и множителей значение произведения не изменится.

3°. Для любых натуральных чисел a, b и c верно равенство abc = (ab)c = a(bc). Это свойство называют сочетательным за-оном умножения, оторый формулируется та : значение произведения не изменится, если а ую-либо руппу множителей заменить их произведением.

4°. При любых значениях a, b и c верно равенство (a + b)c = = ac + bc. Это свойство называют распределительным (дистрибутивным) за оном умножения (относительно сложения), о- торый формулируется та : чтобы умножить сумму на число, достаточно умножить аждое сла аемое на это число и сложить полученные произведения.

Анало ично можно записать: (a – b)c = ac – bc.

6

5. Деление

1°. Разделить число a на число b — значит найти та ое число x, при умножении оторо о на число b получается число a, т. е. a : b = x, если x · b = a.

2°. Число a называют делимым (или ратным) числа b, число b — делителем числа a, число x — частным чисел a и b.

3°. Для натуральных чисел деление нацело не все да выполнимо, т. е. результат деления двух натуральных чисел не все да является натуральным числом.

4°. Призна делимости суммы. Если аждое из сла аемых x и y делится на не оторое число c, то и сумма x + y делится на это число c.

6. Признаки делимости чисел

1°. На 2 и на 5 делятся те и толь о те числа, в записи оторых последняя цифра либо 0, либо выражает число, делящееся соответственно на 2 или на 5.

2°. На 4 или на 25 делятся те и толь о те числа, у оторых две последние цифры — нули или выражают число, делящееся соответственно на 4 или на 25.

3°. На 3 (или на 9) делятся те и толь о те числа, сумма цифроторых делится на 3 (или на 9).

4°. На 10 делятся числа, о анчивающиеся нулем.

5°. Числа, делящиеся на 2, называют четными, а остальные — нечетными.

7. Понятие множества

1°. Одним из фундаментальных понятий математи и является понятие множества. Множество можно представить себеа сово упность (собрание) не оторых объе тов, объединенных по а ому-либо призна у. Множество — понятие неопределяемое.

2°. Множество может состоять из чисел (предметов) и т. п. Каждое число (предмет), входящее в множество, называют элементом множества. Та , множество однозначных чисел состоит из элементов 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

3°. Для записи множества с любыми элементами используют фи урные с об и. Элементы множества можно записать в лю-

7

бом поряд е; например, {2; 3; 1} и {1; 3; 2} — это одно и то же множество, состоящее из чисел 1, 2, 3.

4°. Множества обозначают прописными бу вами латинс о-о алфавита. Например, A = {0; 1; 2; 3; 4; 5; 6; 7; 8; 9} — множество однозначных чисел; число 4 принадлежит множеству A (4 Ý A); число 20 множеству A не принадлежит (20 Ô A).

5°. Множество, оторое не содержит элементов, называют п стым и обозначают символом ¾.

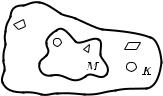
6°. Из рис. 1 видно, что аждый элемент множества M принадлежит та же и множеству K. Еслиаждый элемент одно о множества M является элементом дру о о

множества K, то оворят, что множество M является подмножеством множества K. Это выражается записью M ô K.

7°. Пустое множество ¾ и само множество та же считают подмножествами данно о множества. Та , множество {1; 2; 3} имеет 8 подмножеств: ¾, {1}, {2}, {3}, {1; 2}, {1; 3}, {2; 3}, {1; 2; 3}.

8°. Если аждый элемент множества A является одновременно элементом множества B (т. е. A ô B) и аждый элемент множества B — элементом множества A (т. е. B ô A), то множества A и B называют равными и пишут A = B.

9°. Различают онечные и бес онечные множества. Например, множество всех трехзначных чисел — онечное, а множество N натуральных чисел — бес онечное.

8. Операции над множествами

1°. Пересечением множеств A и B называют множество, состоящее из элементов, оторые принадлежат аждому из данных множеств A и B (рис. 2, а). Пересечение множеств обозначают символом ∩ и пишут C = A ∩ B = {x | x Ý A и x Ý B}.

Пусть, например, A = {1; 2; 5; 7}, B = {3; 5; 7; 8}; то да пересечением этих множеств служит множество C = {5; 7}.

2°. Если множества A и B не имеют общих элементов, то пересечением та их множеств является пустое множество (рис. 2, б).

3°. Объединением множеств A и B называют множество, состоящее из всех элементов множеств A и B и толь о из них. Объединение множеств обозначают символом и пишут

8

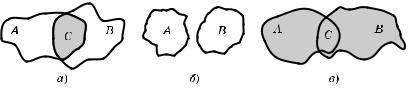
Рис. 2

C = A B = {x | x Ý A или x Ý B} (рис. 2, в). При этом если множества A и B имеют общие элементы, то аждый из этих общих элементов в объединение входит толь о один раз.

Пусть, например, A = {1; 2; 5; 7}, B = {3; 5; 7; 8}; то да объединением этих множеств служит множество D = {1; 2; 3; 5; 7; 8}.

9. Взаимно однозначное соответствие

1°. Если аждому элементу множества A можно поставить в соответствие один и толь о один элемент множества B и, наоборот, аждому элементу множества B можно поставить в соответствие один и толь о один элемент множества A, то та ое соответствие между множествами A и B называют взаимно однозначным.

2°. Если между множествами A и B можно установить взаимно однозначное соответствие, то та ие множества называют

э вивалентными (равносильными).

3°. Установление взаимно однозначно о соответствия дает возможность сравнивать множества с бес онечным числом элементов. Например, между множеством N натуральных чисел и множеством всех четных натуральных чисел можно установить взаимно однозначное соответствие:

Та им образом, эти два множества равносильны.

10. Простые и составные числа

1°. Число a называют простым, если е о делителями являются толь о единица и само число a. Например, числа 2, 3, 5, 13, 29 — простые.

9

2°. Число a, имеющее дру ие делители ( роме 1 и а), называют составным. Например, числа 4, 6, 15 — составные.

Заметим, что число 1 не относят ни простым, ни составным числам.

3°. ОСНОВНАЯ ТЕОРЕМА АРИФМЕТИКИ. Любое составное натуральное число можно представить в виде произведения простых чисел. Например, 12 = 2 · 2 · 3. Говорят та же, что число 12 разложено на простые множители.

Пример. Разложить на простые множители число 525. Р е ш е н и е. Имеем

11. Наибольший общий делитель

1°. Рассмотрим множество A делителей числа 45 и множество B делителей числа 60, т. е. A = {1; 3; 5; 9; 15; 45}; B = {1; 2; 3; 4; 5; 6; 10; 12; 15; 20; 30; 60}. Общими делителями чисел 45 и 60 называют числа, являющиеся элементами а множества A, та и множества B, т. е. элементы пересечения этих множеств: A ∩ B = {1; 3; 5; 15}.

2°. Наибольший из этих элементов (число 15) называют наибольшим общим делителем и обозначают та : НОД(45, 60) = 15.

3°. Если наибольший общий делитель чисел равен 1, то та-ие числа называют взаимно простыми. Например, числа 16 и 25 — взаимно простые, та а НОД(16, 25) = 1.

Пример. Найти НОД(126, 540, 630). Р е ш е н и е. Имеем

10