1.1 Среднее арифметическое (математическое ожидание)

Математическое ожидание имеет простой физический смысл: если на прямой разместить единичную массу, поместив в каждую точку некоторую массу (для дискретного распределения), или «размазав» её с определенной плотностью (для абсолютно непрерывного распределения), то точка будет координатой «центра тяжести» прямой. Среднее арифметическое , этот «центр тяжести», определяется по формуле [7]:

,

где n - количество значений в таблице экспериментальных данных.

Среднее арифметическое вычисляется только для однородных величин.

Для лучшего представления о математическом ожидании изучим его свойства [8]:

. Математическое ожидание постоянной С равно этой постоянной.

. Постоянный множитель можно выносить за знак математического ожидания, т.е.

. Математическое ожидание суммы нескольких случайных величин равно сумме математических ожиданий этих величин:

. Математическое ожидание произведения двух независимых случайных величин равно произведению математических ожиданий этих величин:

Так же можно сказать, что если каждое число, находящееся в таблице измерений, заменить на среднее арифметическое, то общая сумма не изменится.

В данной работе получили среднее значение равное =0,21.

1.2 Дисперсия и среднеквадратическое отклонение случайной величины

Во многих практически важных случаях существенным является вопрос о том, насколько велики отклонения случайной величины от ее математического ожидания. Оценим рассеяние массива экспериментальных данных относительно среднего арифметического значения. Вычисляем несмещенную оценку дисперсии S² по формуле [8]:

Также дисперсией случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.

Вычисляем среднеквадратичное отклонение S (СКО) [8] :

Среднеквадратичное отклонение является, как и дисперсия, мерой рассеяния распределения, но измеряется, в отличие от дисперсии, в тех же единицах, которые используют для измерения значений случайной величины.

Проведя вычисления, получили значения S² = 0,00155, S = 0,1243.

1.3 Третий центральный момент и коэффициент асимметрии

Третий центральный момент, будучи соответствующим образом нормализован, является числовой характеристикой симметрии распределения.

Для того чтобы оценить асимметрию ЗРВ, определяется оценка третьего центрального момента . Оценка третьего момента определяется по формуле [9]:

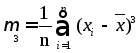
После расчетов получилось =0,000031.

Третий центральный момент и его оценка имеют размерность куба случайной величины, поэтому для относительной характеристики асимметрии применяют безразмерный коэффициент асимметрии s [9]:

где - это СКО в третьей степени.

Рассчитав, получили s=0,016.

Для симметричных ЗРВ относительно математического ожидания =0. Однако в реальности может быть определена только оценка третьего центрального момента, которая, являясь случайной величиной, может приближаться к нулю, но не быть равной ему. Поэтому определяют параметр оценки рассеяния коэффициента асимметрии [9]:

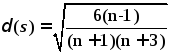
математический ожидание дисперсия гистограмма

Если выполняется условие, что , то можно считать ЗРВ симметричным. Если же это условие не выполняется, то несимметричностью ЗРВ пренебрегать нельзя.

Из моих вычислений следует, что ЗРВ симметричный, так как

.4 Четвертый центральный момент, эксцесс и контрэксцесс

Для того чтобы оценить оценку заостренности ЗРВ, определяют оценку четвертого центрального момента [9]:

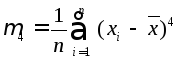
Четвертый центральный момент и его оценка имеют четвертую степень случайной величины, поэтому для удобства применяют относительную величину, называемую эксцессом и определяемую по формуле [9]:

Подставив значения в данные формулы, получили:

=0,00061

=2,5

Для удобства находят и применяют в расчетах оценку контрэксцесса , изменяющуюся от 0 до 1 и определяемую по формуле [9]:

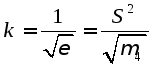
Рассчитав, получила

При подобных значениях эксцесса и контрэксцесса можно сделать предварительный вывод о виде распределения. Можно сказать, что мои расчеты удовлетворяют распределению треугольного вида.

.5 Исключение из массива грубых промахов

Процесс измерения неизбежно сопровождается ошибками, которые вызываются несовершенством измерительных средств, нестабильностью условий проведения измерений, несовершенством самого метода и методики измерений, недостаточным опытом и несовершенством органов чувств человека, выполняющего измерения, а также другими факторами.

Грубая погрешность (промах) - это случайная погрешность результата отдельного наблюдения, входящего в ряд измерений; для данных условий она резко отличается от остальных результатов этого ряда.

Вопрос о том, содержит ли результат наблюдений грубую погрешность, решается общими методами проверки статистических гипотез [8]. Проверяемая гипотеза состоит в утверждении того, что результат наблюдения х не содержит грубой погрешности, то есть является одним из значений входящих в измерение. Используя статистические критерии, пытаются опровергнуть выдвинутую гипотезу. Если это удается, то этот результат рассматривают как грубую погрешность и его исключают, если нет - то результат измерения оставляют.

Выбор того или иного критерия основан на принципе практической уверенности. Известен ряд критериев, которые позволяют исключить грубые промахи [10]. К ним, в частности можно отнести критерий Греббса (Смирнова), Шарлье, Шовенэ, Диксона, Романовского, «трех сигм» и др.

В данной работе для исключения грубых промахов воспользуемся неравенством Чебышева [8], которое утверждает, что случайная величина в основном принимает значения близкие к своему среднему. Более точно, оно даёт оценку вероятности, что случайная величина примет значение далёкое от своего среднего и устанавливает нижнюю границу вероятности того, что ни при каком законе распределения вероятности случайное значение результата измерения не отличается от среднего значения более чем на половину доверительного интервала, определяемого по формуле [8]:

Отсюда можно найти значение t для заданной вероятности:

И границы доверительного интервала:

Но в данном случае целесообразно использовать неравенство, определенное с помощью четвертого центрального момента [10]:

Откуда t определяется следующим образом:

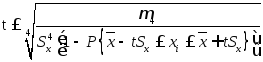
Верхняя и нижняя границы предельных отклонений определяются выражениями:

Результаты измерений, где исчитаются промахами и должны быть исключены из массива данных.

Рассчитываем t для P=0,95, получаем:

Рассчитав значение t, находим верхнюю и нижнюю границы предельных значений отклонений по формулам (1.18) и (1.19):

После сравнения наших экспериментальных данных оказалось, что все значения попадают в данный интервал. Отсюда следует, что наш массив данных не превышает найденный интервал, значит можно сделать вывод, что промахов в массиве данных нет.