
- •Теоретическая часть
- •1. Производная и дифференциал
- •2. Уравнения касательной и нормали
- •3. Правила дифференцирования
- •4. Производные основных элементарных функций
- •5. Производные и дифференциалы высших порядков
- •6. Исследование функции на монотонность и экстремум
- •7. Исследование функции на выпуклость и перегиб
- •Варианты заданий
7. Исследование функции на выпуклость и перегиб
Пусть функция f(x) дифференцируема на <a;b>. Тогда существует касательная к графику функции f(x) в любой точке М(x;f(x)), x<a;b>, причем эти касательные не параллельны оси Оу.
Определение 1. Функция f(x) называется выпуклой вверх (вниз) на <a;b>, если график функции в пределах <a;b> лежит не выше (не ниже) любой из своих касательных.
Теорема 1 (достаточное условие выпуклости). Пусть функция f(x) дважды дифференцируема на <a;b>. Тогда если f (x)0 (f (x)0) на (a;b), то функция выпукла вниз (вверх) на <a;b>.
Определение 2. Пусть f(x) определена и непрерывна в V(x0). Точка x0 называется точкой перегиба функции f(x), если при переходе через эту точку меняется направление выпуклости функции f(x).
Теорема 2 (необходимое условие перегиба). Если в точке перегиба x0 функции f(x) вторая производная существует и непрерывна, то она в этой точке равна нулю.
Теорема
3 (достаточное
условие перегиба). Пусть функция f(x)
дважды дифференцируема в
![]() ,
гдеx0
– точка
возможного перегиба. Если
,
гдеx0
– точка
возможного перегиба. Если
1) f (x) меняет знак при переходе через x0, то x0 - точка перегиба функции f(x);
2) f (x) не меняет знака при переходе через x0, то x0 не является точкой перегиба функции f(x).
Варианты заданий
Задание №1.
Пользуясь определением, найти производную функции:
1.
![]() 4.
4.![]() 7.
7.![]() 10.
10.![]()
2.
![]() 5.
5.![]() 8.
8.![]() 11.
11.![]()
3.
![]() 6.
6.![]() 9.
9.![]() 12.
12.![]()
Задание №2.
Найти дифференциалы функций:
1.
![]()
2.
![]()
3.
![]()
4.

5.
![]()
6.
![]()
7.
![]()
8.
![]()
9.
![]()
10.
![]()
11.
![]()
12.
![]()
13.
![]()
14.
![]()
15.
![]()
16.

17.
![]()
18.
![]()
19.
![]()
20.
![]()
21.
![]()
22.
![]()
23.
![]()
24.
![]()
25.
![]()
26.
![]()
27.
![]()
28.
![]()
29.
![]()
30.
![]()
31.
![]()
32.
![]()
Задание №3.
Найти производную второго порядка функции:
1.
![]() 3.
3.![]() 5.
5.![]() 7.
7.![]()
2.
![]() 4.
4.![]() 6.
6.![]() 8.
8.![]() .
.
Задание №4.
Составить уравнения касательной и нормали к графику функции y=f(x) в точке с абсциссой x0:
1.
![]() ,x0=-1 4.
,x0=-1 4.
![]() ,x0=2 7.
,x0=2 7.
![]() ,x0=1
,x0=1
2.
![]() x0=-1 5.
x0=-1 5.
![]() ,x0=3 8.
,x0=3 8.
![]() ,x0=5
,x0=5
3.
![]() x0=4 6.
x0=4 6.
![]() ,x0=0 9.
,x0=0 9.
![]() ,x0=-2
,x0=-2
Задание №5.
Найти наибольшее и наименьшее значения функции на отрезке:
1.
![]() ,
[0;4]
,
[0;4]
2.
![]() ,
[-2;1]
,
[-2;1]
3.
![]() ,
[-2;2]
,
[-2;2]
4.
![]() ,
,![]()
5.
![]() ,
,![]()
6.
![]() [2;4]
[2;4]
7.
![]() ,
[-1;7]
,
[-1;7]
8.
![]() ,
[-1;2]
,
[-1;2]
9.
![]() ,
[-1;6]
,
[-1;6]
10.
![]() ,
[-4;-1]
,
[-4;-1]
11.
![]() ,
[2;4]
,
[2;4]
12.
![]() ,
[1;9]
,
[1;9]
13.
![]() ,
[-4;2]
,
[-4;2]
14.
![]() ,
[0;4]
,
[0;4]
Задание №6.
Исследовать функцию на монотонность и выпуклость, найти экстремумы и точки перегиба:
1.
![]() 6.
6.![]() 11.
11.![]()
2.
![]() 7.
7.![]() 12.
12.![]()
3.
![]() 8.
8.![]() 13.
13.
![]()
4.
![]() 9.
9.
![]() 14.
14.
![]()
5.
![]() 10.
10.
![]()
Образцы выполнения заданий
Задание №1
Пример 1.
Пользуясь
определением, найти производную
![]() .
.
Решение.
Придадим значению аргумента х приращение х0. Функция y=f(x) получит при этом приращение у=f(x+x)-f(x):
![]()
![]()
![]() .
.
Найдем отношение приращения функции к приращению аргумента:
![]() .
.
Найдем предел этого отношения при х0:
![]() .
.
Следовательно,
по определению производной
![]() .
.
Пример 2.
Пользуясь
определением, найти производную
![]() .
.
Решение.
Придадим
значению аргумента х
приращение х0.
Найдем соответствующее приращение
функции:
![]() .
.
Тогда
![]() .
Вычислим предел этого отношения прих0:
.
Вычислим предел этого отношения прих0:


 .
.
Следовательно,
![]() .
.
Пример 3.
Пользуясь
определением, найти производную
![]() .
.
Решение.
Придадим значению аргумента х приращение х0. Найдем приращение функции:
![]() .
.
Используя
формулу
![]() ,
получим
,
получим
![]() .
.
Тогда
 .
.
И, следовательно,
 .
.
Итак,.![]() .
.
Задание №2
Пример 1.
Найти
дифференциал функции
![]() .
.
Решение.
Перепишем
функцию в виде
![]() .
Воспользуемся правилом дифференцирования
произведения: (uv)=uv+uv.
.
Воспользуемся правилом дифференцирования
произведения: (uv)=uv+uv.
![]() .
.
Тогда
![]() .
.
Пример 2.
Найти
дифференциал функции
![]() ,
|x|<1.
,
|x|<1.
Решение.
Данная
функция является сложной: y=arcsint,
где
![]() .
Применим правило дифференцирования
сложной функции:
.
Применим правило дифференцирования
сложной функции:![]() .
.

 .
.
Тогда
![]() .
.
Пример 3.
Найти
дифференциал функции
![]() .
.
Решение.
Данная
функция является показательно-степенной.
Запишем ее в виде
![]() .
По правилу дифференцирования сложной
функции
.
По правилу дифференцирования сложной
функции![]() ,
гдеt=tgx
ln(sinx).
Тогда
,
гдеt=tgx
ln(sinx).
Тогда
![]()
![]() .
.
Значит,
![]() .
.
Задание №3
Пример.
Найти
производную второго порядка функции
![]() .
.
Решение.
Применяя правила дифференцирования, получим
![]() .
.
Для нахождения второй производной надо продифференцировать первую производную:
![]() .
.
Задание №4
Пример.
Составить
уравнения касательной и нормали к
графику функции
![]() в точке с абсциссойx0=1.
в точке с абсциссойx0=1.
Решение.
Уравнение касательной к графику функции y=f(x) в точке с абсциссой x0 имеет вид
![]() .
.
Вычислим
значение функции в данной точке:
![]() .
.
Найдем производную функции и ее значение в данной точке:
![]() ,
,
![]() .
.
Подставим найденные значения в уравнение касательной:
![]() ,
, ![]() - уравнение касательной.
- уравнение касательной.
Уравнение нормали к графику функции y=f(x) в точке с абсциссой x0 имеет вид
![]() .
.
Подставим найденные значения в это уравнение:
![]() ,
, ![]() - уравнение нормали.
- уравнение нормали.
Задание №5
Пример.
Найти
наибольшее и наименьшее значения функции
![]() на отрезке [2;5].
на отрезке [2;5].
Решение.
1) Найдем критические точки функции.
![]() ,
,
f
(x)=0
![]()
![]()
![]() .
.
На отрезке [2;5] знаменатель не обращается в нуль. Следовательно, дробь равна нулю тогда и только тогда, когда числитель равен нулю:
(x-1)3-8=0 (x-1)3=8 x-1=2 x=3.
Значит, х=3 – критическая точка функции. Она принадлежит данному отрезку.
Найдем
значение функции в критической точке:
![]() .
.
2) Найдем значения функции на концах отрезка:
![]() ,
, ![]() .
.
3) Из полученных значений выбираем наибольшее и наименьшее:
![]() ,
, ![]() .
.
Задание №6
Пример 1.
Исследовать
функцию
![]() на монотонность и выпуклость, найти
экстремумы и точки перегиба.
на монотонность и выпуклость, найти
экстремумы и точки перегиба.
Решение.
Найдем область определения функции.
D(f)=![]() ,
т. к. данная функция – многочлен.
,
т. к. данная функция – многочлен.
Исследуем функцию на монотонность, найдем точки экстремума.
Найдем вначале критические точки функции.
![]()
![]()
![]() .
.
D(f
)=![]() ,
т. к. производная тоже является многочленом.
,
т. к. производная тоже является многочленом.
f (x)=0 x=1 или х=2 или х=3. Следовательно, x=1, х=2, х=3 – критические точки функции.
Н анесем
критические точки функции на числовую
прямую и определим знакипроизводной
в каждом из получившихся промежутков.
анесем
критические точки функции на числовую
прямую и определим знакипроизводной
в каждом из получившихся промежутков.
На промежутках
(-;1], [2;3] функция убывает, на промежутках [1;2], [3;+) функция возрастает.
Точки х=1 и х=3 – точки минимума функции, min f(x)=f(1)=f(3)=0.
Точка х=2 – точка максимума функции, max f(x)=f(2)=1.
Исследуем функцию на выпуклость, найдем точки перегиба.
f (x)=4((x-2)(x-3)+(x-1)(x-3)+(x-1)(x-2))=4(x2-5x+6+x2-4x+3+x2-3x+2)=4(3x2-12x+11).
f (x)=0
3x2-12x+11=0
(x)=0
3x2-12x+11=0
![]() .
.
Нанесем точки х1 и х2 на числовую прямую и определим знаки второй производной в каждом из получившихся промежутков.
На
промежутках
 и
и функция выпукла вниз, на промежутке
функция выпукла вниз, на промежутке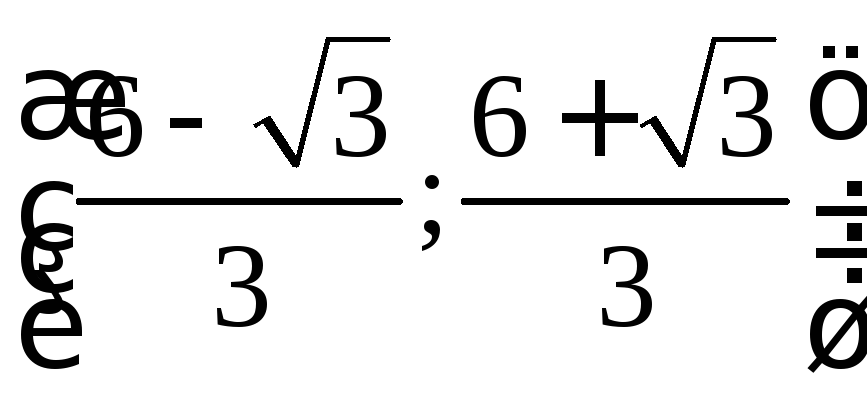 функция выпукла вверх. Точки
функция выпукла вверх. Точки
![]() и
и
![]() являются точками перегиба.
являются точками перегиба.
Пример 2.
Исследовать
функцию
![]() на монотонность и выпуклость, найти
экстремумы и точки перегиба.
на монотонность и выпуклость, найти
экстремумы и точки перегиба.
Решение.
Найдем область определения функции.
D(f):
![]()
![]()
D(f)=(0;1)(1;+).
D(f)=(0;1)(1;+).
2) Исследуем функцию на монотонность, найдем точки экстремума.
 ,
D(f
)=(0;1)(1;+).
,
D(f
)=(0;1)(1;+).
f (x)=0
lnx=1
x=e.
Следовательно, x=e
– критическая
точка функции.
(x)=0
lnx=1
x=e.
Следовательно, x=e
– критическая
точка функции.
Нанесем область определения функции и критическую точку на числовую прямую. Определим знаки производной на каждом из получившихся промежутков.
На промежутках (0;1), (1;e) функция убывает, на промежутке (e, +) функция возрастает. Точка x=e – точка максимума, maxf(x)=f(e)=e.
3) Исследуем функцию на выпуклость, найдем точки перегиба.
 .
.
D(f )=(0;1)(1;+) f (x)=0 lnx=2 x=e2.
Т очкаx=e2
- точка
возможного перегиба. Определим знаки
второй производной в промежутках (0;1),
(1;e2),
(e2;+).
очкаx=e2
- точка
возможного перегиба. Определим знаки
второй производной в промежутках (0;1),
(1;e2),
(e2;+).
На промежутках (0;1), (e2;+) функция выпукла вверх, на промежутке (1;e2) функция выпукла вниз. Точка x=e2 - точка перегиба.
Пример
3.
Провести полное исследование функции
![]() и построить ее график.
и построить ее график.
1)
![]() .
.
2) Функция не является ни четной, ни нечетной, не является периодической.
3) Функция непрерывна на области определения, т.к. является элементарной, х=-3 – точка разрыва. Исследуем характер разрыва:
![]() ,
,
![]() .
.
Следовательно, х=-3 – точка разрыва второго рода, прямая х=-3 – вертикальная асимптота графика функции.
4) Исследуем поведение функции при х+ и при х-:
![]() ,
, ![]() .
.
Следовательно, прямая у=0 – горизонтальная асимптота графика функции при х-. Других наклонных асимптот при х- нет.
5) Выясним, есть ли наклонные асимптоты при х+:
![]() .
.
Следовательно, при х+ наклонных асимптот нет.
6) Исследуем функцию на монотонность и экстремум.
![]()
 ,
,![]()
х=-2 – точка минимума, у(-2)=е – минимум.
7) Исследуем функцию на направление выпуклости и перегиб.



=![]()
 .
.
![]() на
D(f),
y
не существует в точке х=-3.
на
D(f),
y
не существует в точке х=-3.
Т очек
перегиба нет.
очек
перегиба нет.
8) Найдем точки пересечения графика с осями координат и промежутки знакопостоянства.
Ось Ох график не пересекает.
Ось
Оу:
х=0,
![]() .
.
y>0 при x(-3;+), y<0 при x(-;-3).
.
